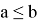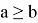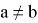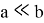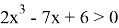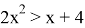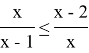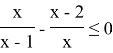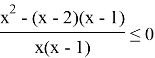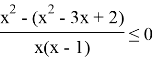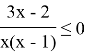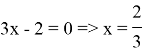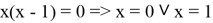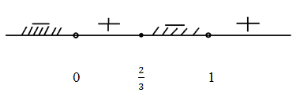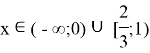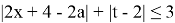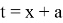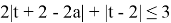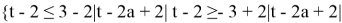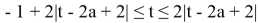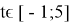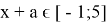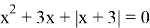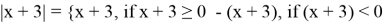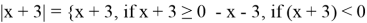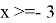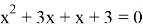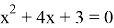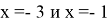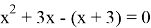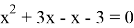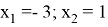Основные ошибки при решении неравенств

Цель исследования данной статьи — определить основные причины, вследствие которых школьники совершают ошибки при решении неравенств; разобрать способы и методы решения некоторых видов неравенств; определить пути исправления возникающих ошибок, а в лучшем случае — вообще не допустить их появления. Рассматриваемая проблема актуальна и по сей день, более того, набирает обороты. И корни ее лежат не вовсе в специфичности конкретно неравенств или любых других видов математических задач. Значит, и пути решения проблемы также стоит искать в несколько более общих областях, о чем мы также поговорим в данной статье.

Ключевые слова:



неравенства, свойства неравенств, правила неравенств.

The purpose of this article is to determine the main reasons why students make mistakes when solving inequalities; to analyze the ways and methods of solving some types of inequalities; to determine ways to correct errors that occur, and in the best case — to prevent them from appearing at all. The problem under consideration is still relevant to this day, moreover, it is gaining momentum. And its roots do not lie in the specificity of specific inequalities or any other types of mathematical problems. This means that you should also look for ways to solve the problem in a few more General areas, which we will also discuss in this article.

Keywords:



inequalities, properties of inequalities, rules of inequalities.

Неравенства

Математика

— наука об отношениях между объектами, о которых не известно ничего, кроме описывающих их некоторых свойств, — собственно эти свойства, качестве аксиом, положены в основание той или иной математической теории. История математики ведется издревле — от простейших операций подсчёта, измерения объектов и описания их формы. Создаются математические объекты с помощью идеализации свойств объектов реальных или других математических и записи этих свойств на формальном языке. К естественным наукам математика не относится, но широко в них используется — как для точной формулировки их содержания, так и для получения новых результатов. Математика — наука фундаментальная, поскольку она предоставляет другим наукам универсальные языковые средства; с помощью этого выявляется взаимосвязь наук, а также находятся общие законы природы.

Что же касается конкретно неравенств, то с ними начинают работать еще с детского сада. Детей учат тому, что в количественном соотношении некоторые объекты больше, а некоторые — меньше других. А есть объекты, которые равны между собой. В начальных классах продолжается изучение неравенств, там сравнивают — в какой чашке больше вишен, какое число больше, а какое меньше, далее следуют более сложные примеры, например — «4+2» больше, меньше или равно «3+3»?

Конечно, чем старше класс, тем сложнее, разнообразнее и интереснее становятся неравенства и пути нахождения их решений. Однако, стоит понимать, что сама суть неравенств и умение ее понимать находятся с человеком на протяжении всей его жизни. Да, мы об этом не задумываемся, но, тем не менее, постоянно решаем эти самые неравенства в своих бытовых делах. В этой пачке больше салфеток, но она стоит дороже, а в этой — меньше, но и стоит она дешевле. Что же выгоднее приобрести? Причем, ведь роль еще играют факторы того, сколько именно нужно сейчас салфеток и пригодятся ли потом лишние… В общем, рассуждать можно долго, этот пример приведен для того, чтобы было понятно — неравенства с нами всю жизнь и, даже если мы не используем математических формул для их решения (по крайней мере, осознанно), тема эта очень важная и актуальная. Тем более острой становится необходимость ее всестороннего изучения в школьной программе. И, как следствие — выявление проблем, трудностей и пробелов, возникающих у учеников. Именно эту проблему и хотелось бы затронуть в данной статье — какие ошибки допускают ученики при решении различных неравенств и какими способами эти ошибки можно исправить или даже избежать их вовсе.

Но прежде чем перейти к проблеме и способам ее решения, стоит немного поговорить о том, что же такое неравенство, каких видов они бывают и какие существуют пути решения.

Итак, что же такое неравенство?

Неравенство

в математике — отношение, связывающее два числа или иных математических объекта с помощью одного из перечисленных ниже знаков.

Строгие неравенства

● — означает, что

меньше

, чем

● — означает, что

больше

, чем

Неравенства равносильны. Говорят, что знаки

противоположны

; например, выражение «знак неравенства сменился на противоположный» означает, что заменено на или наоборот.

Нестрогие неравенства

–

— означает, что

меньше либо равно

–

— означает, что

больше либо равно

Про знаки ⩽ и ⩾ также говорят, что они

противоположны

.

Другие типы неравенств

–

— означает, что

не равно

.

–

— означает, что величина намного больше, чем

–

— означает, что величина намного меньше, чем

Связанные определения

Неравенства с одинаковыми знаками называются

одноимёнными

(иногда используется термин «одного смысла» или «одинакового смысла»). Допускается двойное или даже многократное неравенство, объединяющее несколько неравенств в одно. Пример:— это краткая запись пары неравенств: и

Числовые неравенства

Числовые неравенства содержат вещественные числа (для комплексных чисел сравнение на больше-меньше не определено) и могут содержать также символы неизвестных Числовые неравенства, содержащие неизвестные величины, подразделяются (аналогично уравнениям) на алгебраические и трансцендентные. Алгебраические неравенства, в свою очередь, подразделяются на неравенства первой степени, второй степени и так далее. Например, неравенство — алгебраическое первой степени, неравенство

— алгебраическое третьей степени, неравенство

— трансцендентное.

Существуют определенные правила решения неравенства

При решении неравенств используют следующие правила:

1. Любой член неравенства можно перенести из одной части неравенства в другую с противоположным знаком, при этом знак неравенства не меняется.
2. Обе части неравенства можно умножить или разделить на одно и то же положительное число, не изменив при этом знак неравенства.
3. Обе части неравенства можно умножить или разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный.

Давайте рассмотрим несколько примеров.

1)

Переносим все в одну часть

Приводим к общему знаменателю

Раскрываем скобки, приводим подобные

Находим точки, в которых числитель или знаменатель равны нулю.

Отмечаем х на числовой прямой. Определяем знаки на каждом получившемся промежутке.

Записываем ответ

2)

Заменим

Раскрывая второй из модулей, запишем неравенство в виде системы

или

Ответ:

3)

Раскрываем модуль по определению

I случай

II случай

(не входит в ОДЗ)

Ответ: x=-3; x=-1.

Неравенства включены в ЕГЭ повышенной сложности. Неравенства рассматриваются в 15 пункте под C3. Эти задания рассматриваются в 2 части экзамена, задания с 13–19 с развернутым ответом (полная запись решения с обоснованием выполненных действий), проверяющих освоение математики на профильном уровне, необходимом для применения математики в профессиональной деятельности и на творческом уровне.

Задания части 2 работы предназначены для проверки знаний на том уровне требований, который традиционно предъявляется ВУЗами с профильным экзаменом по математике. Поэтому для более успешной сдачи экзамена, необходимо решить вторую часть, в которую входит тема неравенства.

И вот сейчас, определив и поняв — зачем же нужно уметь решать неравенства, мы переходим к обсуждению обозначенной выше проблемы.

Ошибки, допускаемые обучающимися при решении уравнений и


неравенств.

Ошибки в этой сфере встречается самые разнообразные: от неверного оформления решения до ошибок логического характера.

1. Одна из самых типичных ошибок состоит в том, что учащиеся при решении уравнений и неравенств без дополнительных пояснений используют преобразования, нарушающие равносильность, что приводит к потере корней и появлению посторонних корней.
2. Целая группа ошибок, а точнее будет сказать — недочетов, состоит в том, что учащиеся не уделяют должного внимания нахождению области определения уравнений, хотя именно она в ряде случаев есть ключ к решению.

1. Типичной ошибкой учащихся является то, что они не владеют на нужном уровне определениями понятий, формулами, формулировками теорем, алгоритмами.
2. Многие ошибки, допускаемые при решении уравнений и неравенств, являются следствием того, что учащиеся очень часто пытаются решать задачи по шаблону, привычным путем, даже не задумываясь о том, что стоит посмотреть на задачу с другой стороны.
3. Ряд типичных ошибок связан с тем, что учащиеся не совсем корректно решают уравнения и неравенства на основе функционального подхода.
4. При решении неравенств с помощью подстановки мы всегда сначала решаем новое неравенство относительно новой переменной, и лишь в его решении делаем переход к старой переменной. Школьники же очень часто ошибочно делают обратный переход раньше. Этого делать не следует.
5. Типичная ошибка при решении уравнений, неравенств и их систем состоит в том, что неверно преобразовываются выражения.

Способы исправления и


предупреждения ошибок

Как и в случае с любой проблемой, после ее обозначения и осознания, должны искаться пути решения. Иначе говорить о проблеме становится бессмысленно. Как мы видим, многие ошибки возникают у учащихся в следствие спешки или же невнимательности. А зачастую одно приводит к другому. Поэтому для исправления и предупреждения многих ошибок важно сформировать у школьников навыки

самоконтроля

. Эти навыки состоят из двух частей:

а) умения обнаружить ошибку;

б) умения её объяснить и исправить.

В процессе обучения применяются несколько приёмов самоконтроля, которые помогают обнаружить допущенные ошибки и своевременно их исправить. К ним относятся:

– проверка вычисления и тождественного преобразования путём выполнения обратного действия или преобразования;

– проверка правильности решения задач путём составления и решения задач, обратных к данной;

– оценка результата решения задачи с точки зрения здравого смысла;

– проверка аналитического решения графическим способом.

Сведению вероятности ошибок к минимуму также способствуют следующие профилактические меры:

– Тексты письменных заданий должны быть удобными для восприятия: грамотно сформулированными, хорошо читаемыми.

– Активная устная отработка основных ЗУН, регулярный разбор типичных ошибок.

– При объяснении нового материала предугадать ошибку и подобрать систему заданий на отработку правильного усвоения понятия. Акцентирование внимания на каждом элементе формулы и выполнение разнотипных заданий позволит свести ошибочность к минимуму.

– Подбирать задания, вызывающие интерес, формирующие устойчивое внимание.

– Прочному усвоению (а, значит, отсутствию ошибок) способствуют правила, удобные для запоминания, четкие алгоритмы, следуя которым заведомо придешь к намеченной цели.

Каждый учитель знает, что планомерное и систематическое повторение и есть основной помощник в ликвидации пробелов, а, следовательно, и ошибок. В математике, как ни в какой другой науке, особенно сильна взаимосвязь материала. Изучение и понимание последующего невозможно без знания предыдущего, отсюда возникает неизбежность повторения на каждом уроке. При объяснении нового материала следует использовать ряд определений и теорем, которые были изучены ранее. Тем самым новые знания будут основываться на уже сформировавшейся и закрепившейся базе, что приведет к лучшему усвоению материала. Поэтому так важен, особенно в математике, комплексный и систематический подход к обучению. С самых первых дней обучения важно заложить первые кирпичики той базы, на которую в дальнейшем будут надстраиваться новые знания. Несомненно, главную роль здесь играют способности самого ученика, но проявить и дать направление их развитию — тут уже как раз поле деятельности, которое зависит от таланта и способностей учителя, а также от влияния семьи и окружения. Не только в рассматриваемой сегодня теме, но и в процессе обучения в целом. Ведь, как мы видим, ошибки в решении неравенств возникают именно вследствие пробелов в образовательном процессе в целом, а не из-за специфичности конкретно данного раздела. Так и пути решения и исправления описанных ошибок вовсе не специфичны и уникальны, они сводятся к тому, что сначала надо устранить и/или предупредить общие пробелы в знаниях, не натаскать ребенка на конкретные шаблоны, а именно научить разбираться в рассматриваемом вопросе.

Литература:

1. Математика [Электронный ресурс] / Википедия — Режим доступа: https://goo-gl.ru/6qeR~s
2. Неравенство [Электронный ресурс] / Википедия — Режим доступа: https://goo-gl.ru/6qeV~s
3. Анализ типичных ошибок при решении неравенств [Электронный ресурс] / — Режим доступа: https://goo-gl.ru/6qeW~s
4. Решение неравенств: основные ошибки и полезные лайфхаки [Электронный ресурс] / — Режим доступа: https://goo-gl.ru/6qeY~s
5. Методическое пособие. Неравенства и системы неравенств [Электронный ресурс] / Инфоурок — Режим доступа: https://goo-gl.ru/6qeZ~s
6. https://infourok.ru/user/ivanova-antonina-mihaylovna/blog/problemitipichnie-oshibkidopuskaemie-uchaschimisya-pri-reshenii-uravneniy-i-neravenstv-48897.html

Решение неравенств: основные ошибки и полезные лайфхаки

Вы умеете решать неравенства? Уверены?

Вспомним для начала, что вообще можно делать с неравенствами и чего с ними делать нельзя.

При решении неравенств мы можем:

1. Умножать обе части неравенства на число или выражение, не равное нулю.
При умножении обеих частей неравенства на положительное число знак неравенства сохраняется.

При умножении обеих частей неравенства на отрицательное число знак неравенства меняется на противоположный.

2. Можем возводить обе части неравенства в квадрат при условии, что они неотрицательны

3. Имея дело с показательным или логарифмическим неравенством, мы можем «отбрасывать» основания или логарифмы. Если основание степени или логарифма больше единицы – знак неравенства будет тот же. Если основание степени или логарифма положительно и меньше единицы – знак неравенства меняется на противоположный.

Конечно, мы не просто «отбрасываем» основания степеней или логарифмы. Мы пользуемся свойствами монотонности соответствующих функций. Если основание степени больше единицы, показательная функция монотонно возрастает. Если основание положительно и меньше единицы – показательная функция монотонно убывает. Аналогично ведет себя и логарифмическая функция.

— означает, что

меньше либо равно

–

— означает, что

больше либо равно

Про знаки ⩽ и ⩾ также говорят, что они

противоположны

.

Другие типы неравенств

–

— означает, что

не равно

.

–

— означает, что величина намного больше, чем

–

— означает, что величина намного меньше, чем

Связанные определения

Неравенства с одинаковыми знаками называются

одноимёнными

(иногда используется термин «одного смысла» или «одинакового смысла»). Допускается двойное или даже многократное неравенство, объединяющее несколько неравенств в одно. Пример:— это краткая запись пары неравенств: и

Числовые неравенства

Числовые неравенства содержат вещественные числа (для комплексных чисел сравнение на больше-меньше не определено) и могут содержать также символы неизвестных Числовые неравенства, содержащие неизвестные величины, подразделяются (аналогично уравнениям) на алгебраические и трансцендентные. Алгебраические неравенства, в свою очередь, подразделяются на неравенства первой степени, второй степени и так далее. Например, неравенство — алгебраическое первой степени, неравенство

— алгебраическое третьей степени, неравенство

— трансцендентное.

Существуют определенные правила решения неравенства

При решении неравенств используют следующие правила:

1. Любой член неравенства можно перенести из одной части неравенства в другую с противоположным знаком, при этом знак неравенства не меняется.
2. Обе части неравенства можно умножить или разделить на одно и то же положительное число, не изменив при этом знак неравенства.
3. Обе части неравенства можно умножить или разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный.

Давайте рассмотрим несколько примеров.

1)

Переносим все в одну часть

Приводим к общему знаменателю

Раскрываем скобки, приводим подобные

Находим точки, в которых числитель или знаменатель равны нулю.

Отмечаем х на числовой прямой. Определяем знаки на каждом получившемся промежутке.

Записываем ответ

2)

Заменим

Раскрывая второй из модулей, запишем неравенство в виде системы

или

Ответ:

3)

Раскрываем модуль по определению

I случай

II случай

(не входит в ОДЗ)

Ответ: x=-3; x=-1.

Неравенства включены в ЕГЭ повышенной сложности. Неравенства рассматриваются в 15 пункте под C3. Эти задания рассматриваются в 2 части экзамена, задания с 13–19 с развернутым ответом (полная запись решения с обоснованием выполненных действий), проверяющих освоение математики на профильном уровне, необходимом для применения математики в профессиональной деятельности и на творческом уровне.

Задания части 2 работы предназначены для проверки знаний на том уровне требований, который традиционно предъявляется ВУЗами с профильным экзаменом по математике. Поэтому для более успешной сдачи экзамена, необходимо решить вторую часть, в которую входит тема неравенства.

И вот сейчас, определив и поняв — зачем же нужно уметь решать неравенства, мы переходим к обсуждению обозначенной выше проблемы.

Ошибки, допускаемые обучающимися при решении уравнений и


неравенств.

Ошибки в этой сфере встречается самые разнообразные: от неверного оформления решения до ошибок логического характера.

1. Одна из самых типичных ошибок состоит в том, что учащиеся при решении уравнений и неравенств без дополнительных пояснений используют преобразования, нарушающие равносильность, что приводит к потере корней и появлению посторонних корней.
2. Целая группа ошибок, а точнее будет сказать — недочетов, состоит в том, что учащиеся не уделяют должного внимания нахождению области определения уравнений, хотя именно она в ряде случаев есть ключ к решению.

1. Типичной ошибкой учащихся является то, что они не владеют на нужном уровне определениями понятий, формулами, формулировками теорем, алгоритмами.
2. Многие ошибки, допускаемые при решении уравнений и неравенств, являются следствием того, что учащиеся очень часто пытаются решать задачи по шаблону, привычным путем, даже не задумываясь о том, что стоит посмотреть на задачу с другой стороны.
3. Ряд типичных ошибок связан с тем, что учащиеся не совсем корректно решают уравнения и неравенства на основе функционального подхода.
4. При решении неравенств с помощью подстановки мы всегда сначала решаем новое неравенство относительно новой переменной, и лишь в его решении делаем переход к старой переменной. Школьники же очень часто ошибочно делают обратный переход раньше. Этого делать не следует.
5. Типичная ошибка при решении уравнений, неравенств и их систем состоит в том, что неверно преобразовываются выражения.

Способы исправления и


предупреждения ошибок

Как и в случае с любой проблемой, после ее обозначения и осознания, должны искаться пути решения. Иначе говорить о проблеме становится бессмысленно. Как мы видим, многие ошибки возникают у учащихся в следствие спешки или же невнимательности. А зачастую одно приводит к другому. Поэтому для исправления и предупреждения многих ошибок важно сформировать у школьников навыки

самоконтроля

. Эти навыки состоят из двух частей:

а) умения обнаружить ошибку;

б) умения её объяснить и исправить.

В процессе обучения применяются несколько приёмов самоконтроля, которые помогают обнаружить допущенные ошибки и своевременно их исправить. К ним относятся:

– проверка вычисления и тождественного преобразования путём выполнения обратного действия или преобразования;

– проверка правильности решения задач путём составления и решения задач, обратных к данной;

– оценка результата решения задачи с точки зрения здравого смысла;

– проверка аналитического решения графическим способом.

Сведению вероятности ошибок к минимуму также способствуют следующие профилактические меры:

– Тексты письменных заданий должны быть удобными для восприятия: грамотно сформулированными, хорошо читаемыми.

– Активная устная отработка основных ЗУН, регулярный разбор типичных ошибок.

– При объяснении нового материала предугадать ошибку и подобрать систему заданий на отработку правильного усвоения понятия. Акцентирование внимания на каждом элементе формулы и выполнение разнотипных заданий позволит свести ошибочность к минимуму.

– Подбирать задания, вызывающие интерес, формирующие устойчивое внимание.

– Прочному усвоению (а, значит, отсутствию ошибок) способствуют правила, удобные для запоминания, четкие алгоритмы, следуя которым заведомо придешь к намеченной цели.

Каждый учитель знает, что планомерное и систематическое повторение и есть основной помощник в ликвидации пробелов, а, следовательно, и ошибок. В математике, как ни в какой другой науке, особенно сильна взаимосвязь материала. Изучение и понимание последующего невозможно без знания предыдущего, отсюда возникает неизбежность повторения на каждом уроке. При объяснении нового материала следует использовать ряд определений и теорем, которые были изучены ранее. Тем самым новые знания будут основываться на уже сформировавшейся и закрепившейся базе, что приведет к лучшему усвоению материала. Поэтому так важен, особенно в математике, комплексный и систематический подход к обучению. С самых первых дней обучения важно заложить первые кирпичики той базы, на которую в дальнейшем будут надстраиваться новые знания. Несомненно, главную роль здесь играют способности самого ученика, но проявить и дать направление их развитию — тут уже как раз поле деятельности, которое зависит от таланта и способностей учителя, а также от влияния семьи и окружения. Не только в рассматриваемой сегодня теме, но и в процессе обучения в целом. Ведь, как мы видим, ошибки в решении неравенств возникают именно вследствие пробелов в образовательном процессе в целом, а не из-за специфичности конкретно данного раздела. Так и пути решения и исправления описанных ошибок вовсе не специфичны и уникальны, они сводятся к тому, что сначала надо устранить и/или предупредить общие пробелы в знаниях, не натаскать ребенка на конкретные шаблоны, а именно научить разбираться в рассматриваемом вопросе.

Литература:

1. Математика [Электронный ресурс] / Википедия — Режим доступа: https://goo-gl.ru/6qeR~s
2. Неравенство [Электронный ресурс] / Википедия — Режим доступа: https://goo-gl.ru/6qeV~s
3. Анализ типичных ошибок при решении неравенств [Электронный ресурс] / — Режим доступа: https://goo-gl.ru/6qeW~s
4. Решение неравенств: основные ошибки и полезные лайфхаки [Электронный ресурс] / — Режим доступа: https://goo-gl.ru/6qeY~s
5. Методическое пособие. Неравенства и системы неравенств [Электронный ресурс] / Инфоурок — Режим доступа: https://goo-gl.ru/6qeZ~s
6. https://infourok.ru/user/ivanova-antonina-mihaylovna/blog/problemitipichnie-oshibkidopuskaemie-uchaschimisya-pri-reshenii-uravneniy-i-neravenstv-48897.html

Решение неравенств: основные ошибки и полезные лайфхаки

Вы умеете решать неравенства? Уверены?

Вспомним для начала, что вообще можно делать с неравенствами и чего с ними делать нельзя.

При решении неравенств мы можем:

1. Умножать обе части неравенства на число или выражение, не равное нулю.
При умножении обеих частей неравенства на положительное число знак неравенства сохраняется.

При умножении обеих частей неравенства на отрицательное число знак неравенства меняется на противоположный.

2. Можем возводить обе части неравенства в квадрат при условии, что они неотрицательны

3. Имея дело с показательным или логарифмическим неравенством, мы можем «отбрасывать» основания или логарифмы. Если основание степени или логарифма больше единицы – знак неравенства будет тот же. Если основание степени или логарифма положительно и меньше единицы – знак неравенства меняется на противоположный.

Конечно, мы не просто «отбрасываем» основания степеней или логарифмы. Мы пользуемся свойствами монотонности соответствующих функций. Если основание степени больше единицы, показательная функция монотонно возрастает. Если основание положительно и меньше единицы – показательная функция монотонно убывает. Аналогично ведет себя и логарифмическая функция.

4. При решении показательных или логарифмических неравенств применяется метод рационализации (замены множителя).

5. Общее правило. Если неравенство можно хоть как-то упростить – это необходимо сделать! Иначе его решение может занять восемь страниц и два часа времени.

Чего нельзя делать при решении неравенств? Вот 7 ловушек, в которые часто попадают абитуриенты.

1. Нельзя умножать (или делить) неравенство на выражение, знака которого мы не знаем.

Например, в неравенстве > нельзя поделить левую и правую часть на . Правильный способ: перенести всё в левую часть неравенства, разложить на множители и решить неравенство методом интервалов.

> 0

> 0

Получаем, что < 0 или > . «Сократив» на , который может быть отрицательным, мы не получили бы правильного ответа.

2. Извлекать из неравенства корень тоже нельзя. Такого действия просто нет.

Как, например, решить неравенство

>

Перенесем все в левую часть неравенства, чтобы в правой остался ноль.

> 0

Разложим левую часть на множители.

> 0

Решим неравенство, пользуясь свойствами квадратичной функции , и запишем ответ: < или > .

Запомним: ответы типа « > » абсурдны.

Как решать неравенство > 0? Это типичная «ловушка для абитуриентов». Так и хочется сказать, что > 0 (то есть извлечь корень из неравенства). Но этого делать нельзя. Выражение положительно при всех , кроме нуля. Правильное решение неравенства: .

4. Возводить обе части неравенства в квадрат можно только если они неотрицательны.

5. Помним о том, в каких случаях знак показательного или логарифмического неравенства меняется, а в каких – остается тем же. «Отбрасывая» логарифмы, делаем это грамотно.

6. Если в неравенстве есть дроби, корни четной степени или логарифмы – там обязательно будет область допустимых значений.

7. Сложная тем для старшеклассников – задачи с модулем. Проверьте, умеете ли вы их решать.

При решении неравенств большое значение имеет правильное оформление. Рекомендуется оформлять решение как цепочку равносильных переходов: от исходного неравенства к равносильному ему неравенству или системе.

Обратите внимание на приемы, позволяющие решать неравенства легко, быстро и без лишних вычислений.

А теперь – полезный лайфхак для решения дробно-рациональных неравенств.

Решите неравенство

Запишем ОДЗ:

Что будет, если действовать «по шаблону» — то есть собрать всё в левой части неравенства и привести к одному знаменателю? — Будет много вычислений и выражение четвертой степени.

Может быть, сделаем проще? Представим дробь в виде суммы дробей и .

Продолжаем упрощать левую часть:

Теперь можно и привести дроби к одному знаменателю.

Все, больше ничего не пишем. Решаем неравенство методом интервалов.

Ответ: .

Ошибки, допускаемые обучающимися при решении уравнений и неравенств, самые разнообразные: от неверного оформления решения до ошибок логического характера.

1. Самая типичная ошибка состоит в том, что учащиеся при решении уравнений и неравенств без дополнительных пояснений используют преобразования, нарушающие равносильность, что приводит к потере корней и появлению посторонних корней.

2. Целая группа ошибок, вернее сказать недочетов, состоит в том, что учащиеся не уделяют должного внимания нахождению области определения уравнений, хотя именно она в ряде случаев есть ключ к решению.

3. Типичной ошибкой учащихся является то, что они не владеют на нужном уровне определениями понятий, формулами, формулировками теорем, алгоритмами.

4. Многие ошибки, допускаемые при решении уравнений и неравенств, являются следствием того, что учащиеся очень часто пытаются решать задачи по шаблону, то есть привычным путем.

5. Ряд типичных ошибок связан с тем, что учащиеся не совсем корректно решают уравнения и неравенства на основе функционального подхода. Остановлюсь на типичных ошибки такого рода.

а) Решить уравнение xх = x.

Функция, стоящая в левой части уравнения, – показательно-степенная и раз так, то на основание степени следует наложить такие ограничения: x > 0, x ≠ 1. Прологарифмируем обе части заданного уравнения:

или

Откуда имеем x = 1.

Логарифмирование не привело к сужению области определения исходного уравнения. Но тем не менее произошла потеря двух корней уравнения; непосредственным усмотрением мы находим, что x = 1 и x = –1 являются корнями исходного уравнения.

7. При решении неравенств с помощью подстановки мы всегда сначала решаем новое неравенство относительно новой переменной, и лишь в его решении делаем переход к старой переменной.

Школьники очень часто ошибочно делают обратный переход раньше. Этого делать не следует.

8.Хочу привести пример еще одной ошибки, связанной с решением неравенств.

Решите неравенство

.

Привожу ошибочное решение, которое очень часто предлагают учащиеся.

Возведем обе части исходного неравенства в квадрат. Будем иметь:

,

откуда получаем неверное числовое неравенство , что позволяет сделать вывод: заданное неравенство не имеет решений.

Однако полученный вывод неверен, например, при х = 1000 имеем

, , .

Полученное числовое неравенство верно, а значит х = 1000 является решением.

Значит, заданное неравенство имеет решение, и, следовательно, приведенное выше решение ошибочно.

Привожу правильное решение. Найдем область определения исходного неравенства. Она задается системой

или

откуда .

Ясно, что на интервале (10;1000) нет решений, ибо левая часть заданного неравенства при любом х из этого интервала не имеет смысла.

Рассмотрим два случая.

а) , откуда х > 100. С учетом области определения исходного неравенства имеем промежуток . Для всех х из этого промежутка левая часть исходного неравенства неотрицательна (как значение арифметического квадратного корня), а правая часть – отрицательна. Делаем вывод о том, что – решение заданного неравенства.

б) , откуда . С учетом области определения исходного неравенства имеем промежуток . Для всех х из промежутка имеют смысл обе части неравенства и они имеют неотрицательные значения, значит обе части заданного неравенства мы можем возвести в квадрат. Будем иметь: , откуда . Это неверное числовое неравенство позволяет сделать вывод: значения х из промежутка решениями исходного неравенства не являются.

Ответ: .

9. Типичная ошибка при решении уравнений, неравенств и их систем состоит в том, что неверно преобразовываются выражения.

Большинство ошибок напрямую не связаны с наличием или отсутствием знаний, хотя доведение некоторых вычислительных операций до автоматизма несколько снижает вероятность их появления.

Необходимо осуществлять процесс обучения правилам с помощью специальной модели с использованием приема, активизирующего рефлексивную деятельность учащихся по предупреждению и исправлению ошибок, которые возникают в результате формального усвоения правил.

Самостоятельная работа учащихся над ошибками обеспечивает более осознанный их анализ и анализ собственных действий по решению конкретной задачи, что оказывает благоприятное влияние на качество получаемых знаний и стимулирует развитие логического мышления.

Пример неосознанного применения алгоритма: получив уравнение sin x = 1,2, ученик автоматически ищет его корни по хорошо известной формуле, не обращая внимания на недопустимые значения sin x.

Для исправления и предупреждения многих ошибок важно сформировать у школьников навыки самоконтроля. Выработке навыков самоконтроля помогает и приём приближённой оценки ожидаемого результата.

Каждый учитель знает, что планомерное и систематическое повторение и есть основной помощник в ликвидации пробелов, а, следовательно, и ошибок.

Систематические проверки чужих записей формируют у ученика привычку критически относиться к своему решению. Для этого подходят задания типа «найди ошибку в решении». Процесс отыскания и исправления ошибок самими учащимися под руководством учителя можно сделать поучительным для учащихся.

Самоконтроль

Для исправления и предупреждения многих ошибок важно сформировать у школьников навыки самоконтроля. Эти навыки состоят из двух частей:

а) умения обнаружить ошибку;

б) умения её объяснить и исправить.

В процессе обучения применяются несколько приёмов самоконтроля, которые помогают обнаружить допущенные ошибки и своевременно их исправить. К ним относятся:

• проверка вычисления и тождественного преобразования путём выполнения обратного действия или преобразования;
• проверка правильности решения задач путём составления и решения задач, обратных к данной;
• оценка результата решения задачи с точки зрения здравого смысла;
• проверка аналитического решения графическим способом.

Способы исправления и предупреждения ошибок

Свести ошибки к минимуму способствуют следующие профилактические меры:

• Тексты письменных заданий должны быть удобными для восприятия: грамотно сформулированными, хорошо читаемыми.
• Активная устная отработка основных ЗУН, регулярный разбор типичных ошибок.
• При объяснении нового материала предугадать ошибку и подобрать систему заданий на отработку правильного усвоения понятия. Акцентировать внимание на каждом элементе формулы, выполнение разнотипных заданий позволит свести ошибочность к минимуму.
• Подбирать задания, вызывающие интерес, формирующие устойчивое внимание.
• Прочному усвоению (а значит, отсутствию ошибок) способствуют правила, удобные для запоминания, четкие алгоритмы, следуя которым заведомо придешь к намеченной цели.

Каждый учитель знает, что планомерное и систематическое повторение и есть основной помощник в ликвидации пробелов, а, следовательно, и ошибок. В математике, как ни в какой другой науке, особенно сильна взаимосвязь материала. Изучение и понимание последующего невозможно без знания предыдущего, отсюда неизбежность повторения на каждом уроке. При объяснении нового материала следует использовать ряд определений и теорем, которые были изучены ранее.

math4school.ru

Ошибки в неравенствах

Неравенства по праву считаются одним из самых трудных разделов школьной математики, и при их решении допускается наибольшее количество ошибок. Рассмотрим наиболее часто встречающиеся из них.

Некоторые общие ошибки

Указать наименьшее целое решение неравенства:

х ∈ (4; +∞) , наименьшее целое число 4 .

х ∈ (4; +∞) , наименьшее целое число 5 .

Ответ: если a и b положительные, то a > b ; если a и b отрицательные , то a

Неравенство (х + 5) 2 ≤ 0 выполняется при единственном значении х = –5.

Так как D = 1 2 – 2·2 = –3 ,

Так как старший коэффициент положительный и D , то при любом значении х левая часть неравенства положительна.

Комментарий. Необходимо помнить, что, вообще говоря, нельзя извлекать корень из обеих частей неравенства.

Ошибки в дробно-рациональных неравенствах

Нередко ошибки появляются при сведении неравенств к системе неравенств, совокупности неравенств или совокупности систем неравенств .

K Упражнение. Решить неравенство (large frac>0.)

L Неправильное решение.

Комментарий . Дробь может быть положительной в двух случаях: когда числитель и знаменатель одновременно положительны, и когда числитель и знаменатель отрицательны.

J Правильное решение.

(left[begin begin x + 6 > 0, \ x > 0, end\ begin x + 6 — 6,\ x > 0, end\ begin x 0,;;\ x

Часто учащиеся допускают ошибки при умножении неравенства на знаменатель , который не имеет определенного знака при любых значениях переменной.

K Упражнение 1. Решить неравенство (large frac<2x+3>>1.)

L Неправильное решение.

Комментарий . Нельзя умножать обе части неравенства на знаменатель, который содержит неизвестное, если заранее не известен его знак. Если же вы все-таки не можете обойтись без умножения, то нужно рассматривать два варианта:

J Правильное решение.

Рассмотрим один из возможных способов решения данного неравенства:

(left[begin begin 2 x + 3 > x — 1, \ x — 1 > 0, end\ begin 2 x + 3 — 4,\ x > 1, end\ begin x 1,;;\ x

K Упражнение 2. Решить неравенство (large frac<4-x^2>>0.)

L Неправильное решение.

J Правильное решение.

Так как дробь больше нуля, и числитель принимает положительные значения для любого допустимого значения х , то

K Упражнение 3. Решить неравенство 1 /_x ≥ 2 .

L Неправильное решение.

J Правильное решение.

Так как обе части неравенства представлены стандартными функциями, то легко использовать графические метод решения неравенства:

Очевидно, что значения функции у = 1 /_x достигают 2 и более при х ∈ (0; 1 /₂ ] .

Отметим, что в неравенствах, содержащих переменную в знаменателе, нельзя избавляться от знаменателя даже в том случае, если выписана область допустимых значений. Исключение могут составлять только особые виды неравенств, в которых знаменатель положителен для любых значений переменной. Как, например, (large frac<4+x^2>>0), которое, очевидно, равносильно неравенству х 2 – 81 > 0 , полученному из первого умножением на положительное число 4 + х 2 .

Ошибки при использовании метода интервалов

Рассмотрим типичные ошибки, возникающие при решении неравенств с применением метода интервалов .

K Упражнение 1. Решить неравенство х (х – 6) (х + 1) ≥ 0 .

L Неправильное решение.

Комментарий . В данном решении не учтено, что сравнивается с нулем произведение трех множителей, а не двух. Таким образом, получаются не три интервала, а четыре.

J Правильное решение.

K Упражнение 2. Решить неравенство (х– 5) (х + 3) (2 – х) ≥ 0 .

L Неправильное решение.

Комментарий . В данном примере знаки в интервалах проставлены неверно. Часто учащиеся не задумываясь проставляют знаки, чередуя их справа налево, начиная со знака +.

J Правильное решение.

Числовая ось с проставленными знаками на промежутках должна выглядеть в данном случае следующим образом:

K Упражнение 3. Решить неравенство

(х – (х + 7)	≥ 0.
х + 2

L Неправильное решение.

Комментарий . В дробно-рациональных неравенствах нули знаменателя на числовую ось наносятся пустыми ( выколотыми ) точками , и это не зависит от строгости неравенства.

J Правильное решение.

K Упражнение 4. Решить неравенство (х – 5) (х + 3) 2 ≤ 0 .

L Неправильное решение.

Комментарий . В данном упражнении знаки на интервалах проставлены неверно, так как при переходе через корень четной кратности знак не меняется .

J Правильное решение.

K Упражнение 5. Решить неравенство (х – 1) (х – 10) 2 > 0 .

L Неправильное решение.

Комментарий . При записи ответа к данному неравенству не учтено то, что в точке х = 10 левая часть неравенства обращается в ноль, что не соответствует знаку данного неравенства.

J Правильный ответ: х ∈ (1; 10)∪(10; +∞) .

K Упражнение 6. Решить неравенство (х – 5) 2 (х + 3) ≤ 0 .

L Неправильное решение.

Комментарий . При решении данного неравенства потеряно одно решение. При х = 5 левая часть неравенства обращается в ноль, что тоже удовлетворяет данному неравенству.

J Правильный ответ: х ∈ (–∞; –3]∪<5>.

Ошибки в иррациональных неравенствах

Самый распространенный вид ошибок при решении иррациональных неравенств связан с тем, что учащимися не учитывается область допустимых значений неизвестного для корня четной степени .

K Упражнение. Решить неравенство √ x – 5 .

L Неправильное решение.

Комментарий . Неравенство имеет смысл лишь при x – 5 ≥ 0 .

J Правильное решение.

Нередко учащиеся не учитывают ограничения, которые накладываются на выражения, стоящие вне знака корня четной степени и содержащие неизвестную величину.

K Упражнение 1. Решить неравенство √ 4x + 21 ≤ x + 4 .

L Неправильное решение.

(begin 4x+21leq (x+4)^2,\ 4x+21geq 0; end;; begin 4x+21 leq x^2+8x+16,\ 4xgeq -21; end;; begin x^2+4x-5geq 0,\ xgeq -5,25; end;; begin (x-1)(x+5)geq 0,\ xgeq -5,25. end)

Комментарий . Легко убедиться, что значения х ∈ (–∞; –4) не удовлетворяют данному неравенству.

J Правильное решение.

(begin 4x+21leq (x+4)^2,\ 4x+21geq 0,\ x+4geq 0; end;; begin 4x+21 leq x^2+8x+16,\ 4xgeq -21,\ xgeq -4; end;; begin x^2+4x-5geq 0,\ xgeq -5,25,\ xgeq -4; end;; begin (x-1)(x+5)geq 0,\ xgeq -5,25,\ xgeq -4. end)

K Упражнение 2. Решить неравенство √ x + 26 ≥ x – 4 .

L Неправильное решение.

(begin x+26geq x^2-8x+16,\ x+26geq 0,\ x-4geq 0; end;;; begin x^2-9x-10leq 0,\ xgeq -26,\ xgeq 4; end;;; begin (x+1)(x-10)leq 0,\ xgeq -26,\ xgeq 4. end)

Комментарий . Не рассмотрен случай, когда x – 4 .

J Правильное решение.

(left[beginbegin x+26geq x^2-8x+16,\ x+26geq 0,\ x-4geq 0; end \ begin x+26geq 0,\ x-4

Решением первой системы является промежуток [4; 10] , решением второй – промежуток [–26; 4) . Таким образом, решением совокупности систем является объединение этих промежутков.

Ошибки в показательных и логарифмических неравенствах

При решении показательных и логарифмических неравенств возникновение ошибок, как правило, вызвано тем, что учащиеся неверно применяют свойства показательной и логарифмической функции.

Например, не учитывают, что при положительном, меньшем единицы основании, и показательная, и логарифмическая функции являются убывающими .

K Упражнение. Решить неравенство 0,8 х ≥ 0,8 – 1 /₃ .

L Неправильный ответ: х ≥ – 1 /₃ .

Комментарий . Так как 0 , то при переходе от неравенства степеней с одинаковыми основаниями к неравенству показателей необходимо было поменять знак основания.

J Правильный ответ: х ≤ – 1 /₃ .

Пренебрежение областью допустимых значений неизвестного – еще одна распространенная причина ошибок при решении показательных и, особенно, логарифмических неравенств.

K Упражнение. Решить неравенство log₄ (x 2 + 3x) ≤ 1 .

L Неправильное решение.

J Правильное решение.

Особые затруднения у учащихся вызывают неравенства в которых в основании показательной или логарифмической функции находится переменная . Следует помнить, что при решении таких неравенств нужно рассматривать несколько случаев .

K Упражнение 1. Решить неравенство log_2х (x 2 – 5x + 6) ≤ 1 .

L Неправильное решение.

(begin x > 0, \ x^2-5x+6 > 0, \ x^2-5x+6 leq 2x; end;;;; begin x > 0, \ x^2-5x+6 > 0, \ x^2-7x+6 leq 0; end;;;; begin x > 0, \ (x-2)(x-3) > 0, \ (x-1)(x-6) leq 0. end;;;;)

Комментарий . Ошибка первая: учтены не все ограничения для значений переменной х , содержащейся в основании логарифма. Не только х > 0 , но и х ≠ 0,5 .

Ошибка вторая: так как основание логарифма содержит неизвестный х , необходимо отдельно рассматривать два случая: 0 и 2x > 1 .

J Правильное решение.

(left[begin begin 0 0,\ x^2-5x+6 geq 2x; end\ begin 2x > 1, \ x^2-5x+6 > 0,\ x^2-5x+6 leq 2x; end end right.;;;; left[begin begin 0 0,\ x^2-7x+6 geq 0; end\ begin x > 0,5, \ x^2-5x+6 > 0,\ x^2-7x+6 leq 0; end end right.;;;; left[begin begin 0 0,\ (x-1)(x-6) geq 0; end\ begin x > 0,5, \ (x-2)(x-3) > 0,\ (x-1)(x-6) leq 0. end end right.;;;;)

В первом случае решением системы является промежуток (0; 0,5) , а во втором – объединение промежутков [1; 2)∪(3; 6] .
Таким образом, после объединения ответов получим (0; 0,5)∪[1; 2)∪(3; 6] .

K Упражнение 2. Решить неравенство х 3х + 1 > х 4 .

L Неправильное решение.

J Правильное решение.

При решении неравенств методом замены переменной учащиеся достаточно часто путают, знак совокупности и знак системы , то есть не понимают, что в первом случае решением неравенства является объединение нескольких множеств, а во втором случае – их пересечение.

K Упражнение 1. Решить неравенство lg 2 x + lg x – 2 ≥ 0 .

L Неправильное решение.

(begin t geq 1, \ t leq -2; end;;;; begin lg x geq 1, \ lg x leq -2; end;;;; begin x geq 10, \ x leq 0,01. end;;;;)

Комментарий . Решение должно сводиться к объединению, а не к пересечению двух промежутков, то есть к решению совокупности неравенств.

J Правильное решение.

(left[begin t geq 1,;;;\ t leq -2; end right.;;;; left[begin lg x geq 1,;;;\ lg x leq -2; end right.;;;; begin left[begin x geq 10,;;;\ x leq 0,01; end right. \ ; x > 0. end)

K Упражнение 2. Решить неравенство x – 3 √ x + 2 ≤ 0 .

L Неправильное решение.

(left[begin t geq 1,\ t leq 2; end right.;;;; left[begin sqrt geq 1,\ sqrt leq 2; end right.;;;; left[begin x geq 1,\ x leq 4; end right.;;;; xin (-infty;; +infty).)

Ответ: все числа.

Комментарий . Во-первых, в представленном решении не учтена область допустимых значений переменной, а во-вторых, решение должно сводиться к пересечению двух промежутков, а не к их объединению, то есть к решению системы неравенств или двойного неравенства.

Типичные ошибки и затруднения школьников при решении неравенств различными способами на Едином государственном экзамене по математике Текст научной статьи по специальности « Математика»

Аннотация научной статьи по математике, автор научной работы — Крутихина Марина Викторовна, Зеленина Наталья Алексеевна, Здоровенко Марина Юрьевна

Статья посвящена анализу типичных ошибок и затруднений школьников при решении неравенств различными способами на итоговой аттестации по математике.

Похожие темы научных работ по математике , автор научной работы — Крутихина Марина Викторовна, Зеленина Наталья Алексеевна, Здоровенко Марина Юрьевна

Common mistakes and difficulties students when solving inequalities in a variety of ways on the Unified state exam in mathematics

The article is devoted to the analysis of typical errors and problems school-nicknames when addressing inequalities in different ways on the final examination in mathematics.

Текст научной работы на тему «Типичные ошибки и затруднения школьников при решении неравенств различными способами на Едином государственном экзамене по математике»

научно-методический электронный журнал ART 14296 УДК 372.851

Здоровенко М. Ю., Зеленина Н. А., Крутихина М. В. Типичные ошибки и затруднения школьников при решении неравенств различными способами на Едином государственном экзамене по математике // Концепт. — 2014. — № 10 (октябрь). — ART 14296. -0,5 п. л. — URL: http://e-koncept.ru/2014/14296.htm. -Гос. рег. Эл № ФС 77-49965. — ISSN 2304-120X.

Здоровенко Марина Юрьевна,

кандидат физико-математических наук, доцент кафедры прикладной математики и информатики ФГБОУ ВПО «Вятский государственный университет», г. Киров zdorovenki@ngs.ru

Зеленина Наталья Алексеевна,

кандидат педагогических наук, доцент кафедры фундаментальной и компьютерной математики ФГБОУ ВПО «Вятский государственный гуманитарный университет», г. Киров sezel@mail.ru

Крутихина Марина Викторовна,

кандидат педагогических наук, доцент кафедры фундаментальной и компьютерной математики ФГБОУ ВПО «Вятский государственный гуманитарный университет», г. Киров krumarvik@mail.ru

Типичные ошибки и затруднения школьников при решении неравенств различными способами на Едином государственном экзамене по математике

Аннотация. Статья посвящена анализу типичных ошибок и затруднений школьников при решении неравенств различными способами на итоговой аттестации по математике.

Ключевые слова: обучение математике, неравенство, система неравенств, различные способы решения неравенств, Единый государственный экзамен по математике.

Раздел: (01) педагогика; история педагогики и образования; теория и методика обучения и воспитания (по предметным областям).

Линия уравнений и неравенств является одной из ведущих содержательно-методических линий школьного курса математики. Традиционно наибольшие затруднения у учащихся вызывает решение неравенств. В кодификаторе требований к уровню подготовки выпускников общеобразовательных учреждений для проведения Единого государственного экзамена по математике указано, что учащиеся должны уметь решать рациональные, показательные, логарифмические неравенства и их системы.

В последние годы в модели контрольно-измерительных материалов соответствующее задание содержится в части 2 и имеет повышенный уровень трудности. В частности, в 2014 г. требовалось решить систему, состоящую из логарифмического и показательного неравенств. По данным ЦОКО Кировской области [1], к решению задачи С3 приступило около 35% школьников, что говорит об определенной подготовке по этой теме (к решению задачи С4, например, приступило порядка 7%, С5 — 4% выпускников). Однако дать хотя бы частичное решение системы неравенств, а тем более решить ее полностью удалось далеко не всем. Так, по данным статистики, один первичный балл за решение задачи С3 (обоснованно получен верный ответ в одном неравенстве исходной системы или получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения системы) получили 22,12% учеников, приступивших к решению, два балла (обоснованно получены верные ответы в обоих неравенствах исходной системы) -1,44% школьников. Полные три балла за решение этой задачи (обоснованно полу-

научно-методический электронный журнал ART 14296 УДК 372.851

Здоровенко М. Ю., Зеленина Н. А., Крутихина М. В. Типичные ошибки и затруднения школьников при решении неравенств различными способами на Едином государственном экзамене по математике // Концепт. — 2014. — № 10 (октябрь). — ART 14296. -0,5 п. л. — URL: http://e-koncept.ru/2014/14296.htm. -Гос. рег. Эл № ФС 77-49965. — ISSN 2304-120X.

чен верный ответ) выставлены 6,14% решавших. Средние показатели по стране соответственно равны 34, 8,8, 2,8 и 6,4% [2].

Опыт проверки развернутых ответов участников Единого государственного эк-

замена по математике показывает, что выпускники владеют различными методами решения неравенств, в том числе и выходящими за рамки школьной программы. Вместе с тем можно выделить типичные ошибки и затруднения учащихся при использовании различных способов решения неравенств. Обратимся к анализу этих ошибок на примере решения системы

logii-x(x + 7) • logx+5(9 — х) 0 logx+5(9-x) 0

с11 — х> 1 <х + 7 >1 0 0 х + 5 > 1 9 — х 0 0 1

— —6 10 —7 х > —4 х > 8 х 1 х + 7 0 1 (х + 5 > 1 <9 — х>1 f0 0

о Л —6 — j [10 —4 г—4 8

Л х 0, (X 0, ^1 X > -7,

<9 — х >0. ^ X 2,2>1 и х + 7>2,2>1. Отсюда log11-x(x + 7) > 0 в области допустимых значений.

Следовательно, для того чтобы log11-x(x + 7) • logx+5(9 — х) 1 <9 -х 0 ^

(. х Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

(хе(-5;-4)и(-4;9) U е (-5;-4) и (-4;9) [х е (-5;-4) и (-4;9)

Определим знак функции в каждом промежутке ее области определения:

Если х = 8,5, тогда log2i515,5 • 1од1350,5 0.

Если х = -4,5, тогда 1од1552,5 • 1од0513,5 0

/орц-х(х + 7) • /орх+5(9 — х) 0

и далее рационализировали каждое из четырех неравенств, исходя при этом из того, что знак логарифмической функции в ее области определения совпадает со знаком соответствующего рационального выражения (знак выражения /ор5/ совпадает со знаком выражения (р — 1)(/ — 1) в области определения логарифмической функции).

Рационализацию для решения логарифмического неравенства выбирают примерно 20% учащихся из числа приступивших к решению.

Показательное неравенство 64*2-3х+20 — 0Д252*2-6*-200 0) в области его допустимых значений совпадает со знаком выражения (Л — 1)(/ — р).

В нашем случае 26*2-18х+120 — 2-6*2+18х+600 /о$9(10 — х).

Наш опыт проверки работ участников ЕГЭ позволяет предположить, что предложенный разработчиками путь решения школьники, скорее всего, не выберут.

Рассмотрим наиболее ожидаемые способы рассуждений учащихся при решении этого неравенства.

Найдем область допустимых значений неравенства:

г х + 2 > 0, х — 1 > 0,

/о#х-1(х + 2) • 2/о$3|х — 1| — /о$3(10 — х) > 0;

Учитывая, что в области допустимых значений неравенства |х — 1| = х — 1, и применяя формулу перехода к новому основанию, получаем

Решение неравенств: основные ошибки и полезные лайфхаки

Вы умеете решать неравенства? Уверены?

Вспомним для начала, что вообще можно делать с неравенствами и чего с ними делать нельзя.

При решении неравенств мы можем:

1. Умножать обе части неравенства на число или выражение, не равное нулю.
При умножении обеих частей неравенства на положительное число знак неравенства сохраняется.

При умножении обеих частей неравенства на отрицательное число знак неравенства меняется на противоположный.

2. Можем возводить обе части неравенства в квадрат при условии, что они неотрицательны

3. Имея дело с показательным или логарифмическим неравенством, мы можем «отбрасывать» основания или логарифмы. Если основание степени или логарифма больше единицы – знак неравенства будет тот же. Если основание степени или логарифма положительно и меньше единицы – знак неравенства меняется на противоположный.

Конечно, мы не просто «отбрасываем» основания степеней или логарифмы. Мы пользуемся свойствами монотонности соответствующих функций. Если основание степени больше единицы, показательная функция монотонно возрастает. Если основание положительно и меньше единицы – показательная функция монотонно убывает. Аналогично ведет себя и логарифмическая функция.

4. При решении показательных или логарифмических неравенств применяется метод рационализации (замены множителя).

5. Общее правило. Если неравенство можно хоть как-то упростить – это необходимо сделать! Иначе его решение может занять восемь страниц и два часа времени.

Чего нельзя делать при решении неравенств? Вот 7 ловушек, в которые часто попадают абитуриенты.

1. Нельзя умножать (или делить) неравенство на выражение, знака которого мы не знаем.

Например, в неравенстве > нельзя поделить левую и правую часть на . Правильный способ: перенести всё в левую часть неравенства, разложить на множители и решить неравенство методом интервалов.

Получаем, что . «Сократив» на , который может быть отрицательным, мы не получили бы правильного ответа.

2. Извлекать из неравенства корень тоже нельзя. Такого действия просто нет.

Как, например, решить неравенство

Перенесем все в левую часть неравенства, чтобы в правой остался ноль.

Разложим левую часть на множители.

Решим неравенство, пользуясь свойствами квадратичной функции , и запишем ответ: .

Запомним: ответы типа « > » абсурдны.

Как решать неравенство > 0? Это типичная «ловушка для абитуриентов». Так и хочется сказать, что > 0 (то есть извлечь корень из неравенства). Но этого делать нельзя. Выражение положительно при всех , кроме нуля. Правильное решение неравенства: .

4. Возводить обе части неравенства в квадрат можно только если они неотрицательны.

5. Помним о том, в каких случаях знак показательного или логарифмического неравенства меняется, а в каких – остается тем же. «Отбрасывая» логарифмы, делаем это грамотно.

6. Если в неравенстве есть дроби, корни четной степени или логарифмы – там обязательно будет область допустимых значений.

7. Сложная тем для старшеклассников – задачи с модулем. Проверьте, умеете ли вы их решать.

При решении неравенств большое значение имеет правильное оформление. Рекомендуется оформлять решение как цепочку равносильных переходов: от исходного неравенства к равносильному ему неравенству или системе.

Обратите внимание на приемы, позволяющие решать неравенства легко, быстро и без лишних вычислений.

А теперь – полезный лайфхак для решения дробно-рациональных неравенств.

Что будет, если действовать «по шаблону» — то есть собрать всё в левой части неравенства и привести к одному знаменателю? — Будет много вычислений и выражение четвертой степени.

Может быть, сделаем проще? Представим дробь в виде суммы дробей и .

Продолжаем упрощать левую часть:

Теперь можно и привести дроби к одному знаменателю.

Все, больше ничего не пишем. Решаем неравенство методом интервалов.