-
Оценка случайной погрешности
Случайную
погрешность величины Xможно оценить,
только проведямногократые измеренияX– не менеечетырёх измерений.
Это означает, что процедуру измеренияXнадо проделать не менее четырёх
раз, причём обязательно в одних и
тех же условиях1.
Если бы никакие случайные факторы не
влияли на результаты измерений, то
сколько бы раз не повторялась процедура
измеренияX, все результаты были бы
совершенно идентичными. Наличие случайных
факторов приводит к тому, что серия изnизмерений даётnразных значений
величиныX: (x,x, …,xn)2.
То, насколько велик разброс в этихnчислах, и определяет случайную погрешность.
Формула, по которой оценивают случайную
погрешностьс(x),
имеет вид:
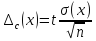
Здесь
величина tназываетсякоэффициентом
Стьюдента. Как его определить,
рассмотрено в пункте 1.6. Величина(x)
называетсясреднеквадратичным(илистандартным) отклонением и определяется
выражением
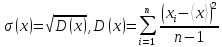
где
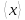
среднее арифметическое изnчиселx,x,
…,xn:
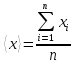
а
число D(x)
называется дисперсией3.
В пункте 1.6
отмечается, что с ростом объёма серии
nкоэффициент Стьюдента уменьшается.
Поэтому из формулы (1.7) вытекает:чем
больше объём серии, тем меньше случайная
погрешность. Обычно объём серии
выбирают так, чтобы случайная погрешность
былав три-пять раз меньшеприборной
погрешности.
-
Доверительная вероятность и коэффициент Стьюдента
Будем в этом
пункте считать, что приборная погрешность
равна нулю. Тогда 2c– этоширина доверительного интервала.
В пункте 1.1 предполагалось, что в центре
доверительного интервала находитсяистинное значениеxизмеряемой величиныX. Истинное
значение, однако, неизвестно, поэтому
передвинем доверительный интервал так,
чтобы в центре его находилосьсреднее
значениерезультатов измерения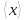
Вероятность того, что истинное значение
x
измеряемой величиныXпринадлежит
доверительному интервалу шириной 2сс центром в точке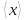
называетсядоверительной вероятностьюилинадёжностью измерений.
Ясно, что чем
шире доверительный интервал 2с,
тем больше и доверительная вероятностьp. Верно и обратное:
чем больше требование к надёжности
измеренийp, тем больше
и значение случайной погрешностис.
Связь междуpисопределяется формулой (1.7), в которой
коэффициент Стьюдентаtзависит от доверительной вероятностиp.
Таблица
1.1.
Коэффициенты Стьюдента
|
Объём серии n |
Доверительная вероятность p |
|||||||
|
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
0,95 |
0,98 |
0,99 |
|
|
4 |
0,77 |
0,98 |
1,2 |
1,6 |
2,4 |
3,2 |
4,5 |
5,8 |
|
5 |
0,74 |
0,94 |
1,2 |
1,5 |
2,1 |
2,8 |
3,7 |
4,6 |
|
6 |
0,73 |
0,92 |
1,2 |
1,5 |
2,0 |
2,6 |
3,4 |
4,0 |
|
7 |
0,72 |
0,90 |
1,1 |
1,4 |
1,9 |
2,4 |
3,1 |
3,7 |
|
8 |
0,71 |
0,90 |
1,1 |
1,4 |
1,9 |
2,4 |
3,0 |
3,5 |
|
9 |
0,71 |
0,89 |
1,1 |
1,4 |
1,8 |
2,3 |
2,9 |
3,4 |
|
10 |
0,70 |
0,88 |
1,1 |
1,4 |
1,8 |
2,3 |
2,8 |
3,3 |
|
15 |
0,69 |
0,87 |
1,1 |
1,3 |
1,8 |
2,1 |
2,6 |
3,0 |
|
20 |
0,69 |
0,86 |
1,1 |
1,3 |
1,7 |
2,1 |
2,5 |
2,9 |
Как видно из
таблицы 1.1, на коэффициент Стьюдента
влияет, кроме доверительной вероятности,
ещё и объём серии n: чем большеn,
тем меньшеt. В учебном
лабораторном практикуме рекомендуется
выбирать значение доверительной
вероятностиp= 0,9, а
объём серииn– от 5 до 10.
Пример.
Требуется измерить сопротивление
резистораRс надёжностьюp= 0,9. Для этого подготовлена таблица 1.2,
а затем проделана серия из 10 измерений,
полученные значения (частныерезультаты) записаны во втором столбце
таблицы. Внизу столбца записано среднее
значение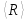
которое и считаетсяконечнымрезультатом измерения сопротивления.
Таблица
1.2.
Соседние файлы в папке Пособия к лаб. работам
- #
- #
Обновлено: 08.06.2023
Свойства физического объекта (явления, процесса) определяются набором количественных характеристик — физических величин . Как правило, результат измерения представляет собой число , задающее отношение измеряемой величины к некоторому эталону . Сравнение с эталоном может быть как прямым (проводится непосредственно экспериментатором), так и косвенным (проводится с помощью некоторого прибора, которому экспериментатор доверяет). Полученные таким образом величины имеют размерность , определяемую выбором эталона.
Замечание. Результатом измерения может также служить количество отсчётов некоторого события, логическое утверждение (да/нет) или даже качественная оценка (сильно/слабо/умеренно). Мы ограничимся наиболее типичным для физики случаем, когда результат измерения может быть представлен в виде числа или набора чисел .
Взаимосвязь между различными физическими величинами может быть описана физическими законами , представляющими собой идеализированную модель действительности. Конечной целью любого физического эксперимента (в том числе и учебного) является проверка адекватности или уточнение параметров таких моделей.
1.1 Результат измерения
Рассмотрим простейший пример: измерение длины стержня с помощью линейки. Линейка проградуирована производителем с помощью некоторого эталона длины — таким образом, сравнивая длину стержня с ценой деления линейки, мы выполняем косвенное сравнение с общепринятым стандартным эталоном.
Допустим, мы приложили линейку к стержню и увидели на шкале некоторый результат x = x изм . Можно ли утверждать, что x изм — это длина стержня?
Во-вторых, мы никак не можем быть уверенны, что длина стержня на самом деле такова хотя бы с точностью до ошибки округления. Действительно, мы могли приложить линейку не вполне ровно; сама линейка могла быть изготовлена не вполне точно; стержень может быть не идеально цилиндрическим и т.п.
Итак, из нашего примера видно, что никакое физическое измерение не может быть произведено абсолютно точно, то есть у любого измерения есть погрешность .
Об измеренной величине также часто говорят как об оценке , подчеркивая, что эта величина не точна и зависит не только от физических свойств исследуемого объекта, но и от процедуры измерения.
Замечание. Термин оценка имеет и более формальное значение. Оценкой называют результат процедуры получения значения параметра или параметров физической модели, а также иногда саму процедуру. Теория оценок является подразделом математической статистики. Некоторые ее положения изложены в главе 3 , но для более серьезного понимания следует обратиться к [ 5 ] .
где δ x — абсолютная величина погрешности. Эта запись означает, что исследуемая величина лежит в интервале x ∈ ( x изм — δ x ; x изм + δ x ) с некоторой достаточно большой долей вероятности (более подробно о вероятностном содержании интервалов см. п. 2.2 ). Для наглядной оценки точности измерения удобно также использовать относительную величину погрешности:
Она показывает, насколько погрешность мала по сравнению с самой измеряемой величиной (её также можно выразить в процентах: ε = δ x x ⋅ 100 % ).
Пример. Штангенциркуль — прибор для измерения длин с ценой деления 0 , 1 мм . Пусть диаметр некоторой проволоки равен 0 , 37 мм. Считая, что абсолютная ошибка составляет половину цены деления прибора, результат измерения можно будет записать как d = 0 , 40 ± 0 , 05 мм (или d = ( 40 ± 5 ) ⋅ 10 — 5 м ). Относительная погрешность составляет ε ≈ 13 % , то есть точность измерения весьма посредственная — поскольку размер объекта близок к пределу точности прибора.
О необходимости оценки погрешностей.
Измерим длины двух стержней x 1 и x 2 и сравним результаты. Можно ли сказать, что стержни одинаковы или различны?
Казалось бы, достаточно проверить, справедливо ли x 1 = x 2 . Но никакие два результата измерения не равны друг другу с абсолютной точностью! Таким образом, без указания погрешности измерения ответ на этот вопрос дать невозможно .
С другой стороны, если погрешность δ x известна, то можно утверждать, что если измеренные длины одинаковы в пределах погрешности опыта , если | x 2 — x 1 | δ x (и различны в противоположном случае).
Итак, без знания погрешностей невозможно сравнить между собой никакие два измерения, и, следовательно, невозможно сделать никаких значимых выводов по результатам эксперимента: ни о наличии зависимостей между величинами, ни о практической применимости какой-либо теории, и т. п. В связи с этим задача правильной оценки погрешностей является крайне важной, поскольку существенное занижение или завышение значения погрешности (по сравнению с реальной точностью измерений) ведёт к неправильным выводам .
В физическом эксперименте (в том числе лабораторном практикуме) оценка погрешностей должна проводиться всегда (даже когда составители задания забыли упомянуть об этом).
1.2 Многократные измерения
Проведём серию из n одинаковых ( однотипных ) измерений одной и той же физической величины (например, многократно приложим линейку к стержню) и получим ряд значений
Что можно сказать о данном наборе чисел и о длине стержня? И можно ли увеличивая число измерений улучшить конечный результат?
Если цена деления самой линейки достаточно мала, то как нетрудно убедиться на практике, величины < x i >почти наверняка окажутся различными . Причиной тому могут быть самые разные обстоятельства, например: у нас недостаточно остроты зрения и точности рук, чтобы каждый раз прикладывать линейку одинаково; стенки стержня могут быть слегка неровными; у стержня может и не быть определённой длины, например, если в нём возбуждены звуковые волны, из-за чего его торцы колеблются, и т. д.
В такой ситуации результат измерения интерпретируется как случайная величина , описываемая некоторым вероятностным законом ( распределением ). Подробнее о случайных величинах и методах работы с ними см. гл. 2 .
По набору результатов 𝐱 можно вычислить их среднее арифметическое:
| ⟨ x ⟩ = x 1 + x 2 + … + x n n ≡ 1 n ∑ i = 1 n x i . | (1.1) |
Это значение, вычисленное по результатам конечного числа n измерений, принято называть выборочным средним. Здесь и далее для обозначения выборочных средних будем использовать угловые скобки.
Кроме среднего представляет интерес и то, насколько сильно варьируются результаты от опыта к опыту. Определим отклонение каждого измерения от среднего как
Δ x i = x i — ⟨ x ⟩ , i = 1 … n .
Разброс данных относительно среднего принято характеризовать среднеквадратичным отклонением :
| s = Δ x 1 2 + Δ x 2 2 + … + Δ x n 2 n = 1 n ∑ i = 1 n Δ x i 2 | (1.2) |
| s 2 = ⟨ ( x — ⟨ x ⟩ ) 2 ⟩ . | (1.3) |
Значение среднего квадрата отклонения s 2 называют выборочной дисперсией .
Будем увеличивать число измерений n ( n → ∞ ). Если объект измерения и методика достаточно стабильны, то отклонения от среднего Δ x i будут, во-первых, относительно малы, а во-вторых, положительные и отрицательные отклонения будут встречаться примерно одинаково часто. Тогда при вычислении ( 1.1 ) почти все отклонения Δ x i скомпенсируются и можно ожидать, что выборочное среднее при n ≫ 1 будет стремиться к некоторому пределу:
lim n → ∞ 1 n ∑ i = 1 n x i = x ¯ .
Предельную величину среднеквадратичного отклонения при n → ∞ обозначим как
lim n → ∞ 1 n ∑ i = 1 n Δ x i 2 = σ .
Замечание. В общем случае указанные пределы могут и не существовать. Например, если измеряемый параметр меняется во времени или в результате самого измерения, либо испытывает слишком большие случайные скачки и т. п. Такие ситуации требуют особого рассмотрения и мы на них не останавливаемся.
Замечание. Если n мало ( n 10 ), для оценки среднеквадратичного отклонения математическая статистика рекомендует вместо формулы ( 1.3 ) использовать исправленную формулу (подробнее см. п. 5.2 ): s n — 1 2 = 1 n — 1 ∑ i = 1 n Δ x i 2 , (1.4) где произведена замена n → n — 1 . Величину s n — 1 часто называют стандартным отклонением .
Итак, можно по крайней мере надеяться на то, что результаты небольшого числа измерений имеют не слишком большой разброс, так что величина ⟨ x ⟩ может быть использована как приближенное значение ( оценка ) истинного значения ⟨ x ⟩ ≈ x ¯ , а увеличение числа измерений позволит уточнить результат.
Многие случайные величины подчиняются так называемому нормальному закону распределения (подробнее см. Главу 2 ). Для таких величин могут быть строго доказаны следующие свойства:
при многократном повторении эксперимента бо́льшая часть измерений ( ∼ 68%) попадает в интервал x ¯ — σ x x ¯ + σ (см. п. 2.2 ).
выборочное среднее значение ⟨ x ⟩ оказывается с большей вероятностью ближе к истинному значению x ¯ , чем каждое из измерений < x i >в отдельности. При этом ошибка вычисления среднего убывает пропорционально корню из числа опытов n (см. п. 2.4 ).
Упражнение. Показать, что s 2 = ⟨ x 2 ⟩ — ⟨ x ⟩ 2 . (1.5) то есть дисперсия равна разности среднего значения квадрата ⟨ x 2 ⟩ = 1 n ∑ i = 1 n x i 2 и квадрата среднего ⟨ x ⟩ 2 = ( 1 n ∑ i = 1 n x i ) 2 .
1.3 Классификация погрешностей
Чтобы лучше разобраться в том, нужно ли многократно повторять измерения, и в каком случае это позволит улучшить результаты опыта, проанализируем источники и виды погрешностей.
В первую очередь, многократные измерения позволяют проверить воспроизводимость результатов: повторные измерения в одинаковых условиях, должны давать близкие результаты. В противном случае исследование будет существенно затруднено, если вообще возможно. Таким образом, многократные измерения необходимы для того, чтобы убедиться как в надёжности методики, так и в существовании измеряемой величины как таковой.
Замечание. Часто причины аномальных отклонений невозможно установить на этапе обработки данных, поскольку часть информации о проведении измерений к этому моменту утеряна. Единственным способ борьбы с этим — это максимально подробное описание всего процесса измерений в лабораторном журнале . Подробнее об этом см. п. 4.1.1 .
При многократном повторении измерении одной и той же физической величины погрешности могут иметь систематический либо случайный характер. Назовём погрешность систематической , если она повторяется от опыта к опыту, сохраняя свой знак и величину, либо закономерно меняется в процессе измерений. Случайные (или статистические ) погрешности меняются хаотично при повторении измерений как по величине, так и по знаку, и в изменениях не прослеживается какой-либо закономерности.
Кроме того, удобно разделять погрешности по их происхождению. Можно выделить
инструментальные (или приборные ) погрешности , связанные с несовершенством конструкции (неточности, допущенные при изготовлении или вследствие старения), ошибками калибровки или ненормативными условиями эксплуатации измерительных приборов;
методические погрешности , связанные с несовершенством теоретической модели явления (использование приближенных формул и моделей явления) или с несовершенством методики измерения (например, влиянием взаимодействия прибора и объекта измерения на результат измерения);
1.3.1 Случайные погрешности
Случайный характер присущ большому количеству различных физических явлений, и в той или иной степени проявляется в работе всех без исключения приборов. Случайные погрешности обнаруживаются просто при многократном повторении опыта — в виде хаотичных изменений ( флуктуаций ) значений < x i >.
Если случайные отклонения от среднего в большую или меньшую стороны примерно равновероятны, можно рассчитывать, что при вычислении среднего арифметического ( 1.1 ) эти отклонения скомпенсируются, и погрешность результирующего значения ⟨ x ⟩ будем меньше, чем погрешность отдельного измерения.
Случайные погрешности бывают связаны, например,
с особенностями используемых приборов : техническими недостатками (люфт в механических приспособлениях, сухое трение в креплении стрелки прибора), с естественными (тепловой и дробовой шумы в электрических цепях, тепловые флуктуации и колебания измерительных устройств из-за хаотического движения молекул, космическое излучение) или техногенными факторами (тряска, электромагнитные помехи и наводки);
с особенностями и несовершенством методики измерения (ошибка при отсчёте по шкале, ошибка времени реакции при измерениях с секундомером);
с несовершенством объекта измерений (неровная поверхность, неоднородность состава);
со случайным характером исследуемого явления (радиоактивный распад, броуновское движение).
1.3.2 Систематические погрешности
Систематические погрешности, в отличие от случайных, невозможно обнаружить, исключить или уменьшить просто многократным повторением измерений. Они могут быть обусловлены, во-первых, неправильной работой приборов ( инструментальная погрешность ), например, сдвигом нуля отсчёта по шкале, деформацией шкалы, неправильной калибровкой, искажениями из-за не нормативных условий эксплуатации, искажениями из-за износа или деформации деталей прибора, изменением параметров прибора во времени из-за нагрева и т.п. Во-вторых, их причиной может быть ошибка в интерпретации результатов ( методическая погрешность ), например, из-за использования слишком идеализированной физической модели явления, которая не учитывает некоторые значимые факторы (так, при взвешивании тел малой плотности в атмосфере необходимо учитывать силу Архимеда; при измерениях в электрических цепях может быть необходим учет неидеальности амперметров и вольтметров и т. д.).
Систематические погрешности условно можно разделить на следующие категории.
Известные погрешности, которые могут быть достаточно точно вычислены или измерены. При необходимости они могут быть учтены непосредственно: внесением поправок в расчётные формулы или в результаты измерений. Если они малы, их можно отбросить, чтобы упростить вычисления.
Погрешности известной природы, конкретная величина которых неизвестна, но максимальное значение вносимой ошибки может быть оценено теоретически или экспериментально. Такие погрешности неизбежно присутствуют в любом опыте, и задача экспериментатора — свести их к минимуму, совершенствуя методики измерения и выбирая более совершенные приборы.
Чтобы оценить величину систематических погрешностей опыта, необходимо учесть паспортную точность приборов (производитель, как правило, гарантирует, что погрешность прибора не превосходит некоторой величины), проанализировать особенности методики измерения, и по возможности, провести контрольные опыты.
Погрешности известной природы, оценка величины которых по каким-либо причинам затруднена (например, сопротивление контактов при подключении электронных приборов). Такие погрешности должны быть обязательно исключены посредством модификации методики измерения или замены приборов.
Наконец, нельзя забывать о возможности существования ошибок, о которых мы не подозреваем, но которые могут существенно искажать результаты измерений. Такие погрешности самые опасные, а исключить их можно только многократной независимой проверкой измерений, разными методами и в разных условиях.
В учебном практикуме учёт систематических погрешностей ограничивается, как правило, паспортными погрешностями приборов и теоретическими поправками к упрощенной модели исследуемого явления.
Точный учет систематической ошибки возможен только при учете специфики конкретного эксперимента. Особенное внимание надо обратить на зависимость (корреляцию) систематических смещений при повторных измерениях. Одна и та же погрешность в разных случаях может быть интерпретирована и как случайная, и как систематическая.
Пример. Калибровка электромагнита производится при помощи внесения в него датчика Холла или другого измерителя магнитного потока. При последовательных измерениях с разными токами (и соотственно полями в зазоре) калибровку можно учитыать двумя различными способами: • Измерить значение поля для разных токов, построить линейную калибровочную кривую и потом использовать значения, восстановленные по этой кривой для вычисления поля по току, используемому в измерениях. • Для каждого измерения проводить допольнительное измерения поля и вообще не испльзовать значения тока. В первом случае погрешность полученного значения будет меньше, поскльку при проведении прямой, отдельные отклонения усреднятся. При этом погрешность измерения поля будет носить систематический харрактер и при обработке данных ее надо будет учитывать в последний момент. Во втором случае погрешность будет носить статистический (случайный) харрактер и ее надо будет добавить к погрешности каждой измеряемой точки. При этом сама погрешность будет больше. Выбор той или иной методики зависит от конретной ситуации. При большом количестве измерений, второй способ более надежный, поскольку статистическая ошибка при усреднении уменьшается пропорционально корню из количества измерений. Кроме того, такой способ повзоляет избежать методической ошибки, связанной с тем, что зависимость поля от тока не является линейной.
Пример. Рассмотрим измерение напряжения по стрелочному вольтметру. В показаниях прибора будет присутствовать три типа погрешности: 1. Статистическая погрешность, связанная с дрожанием стрелки и ошибкой визуального наблюдения, примерно равная половине цены деления. 2. Систематическая погрешность, связанная с неправильной установкой нуля. 3. Систематическая погрешность, связанная с неправильным коэффициентом пропорциональности между напряжением и отклонением стрелки. Как правило приборы сконструированы таким образом, чтобы максимальное значение этой погрешности было так же равно половине цены деления (хотя это и не гарантируется).
Читайте также:
- Строма это в биологии кратко
- Пермь в судьбе декабристов кратко
- Русско литовская война 1500 1503 кратко
- Поэзия древнего китая кратко
- Матрена тимофеевна идеал величавой славянки или простая русская баба кратко
Случайные погрешности в лабораторных работах по физике можно оценивать только с использованием калькулятора
О теории случайных погрешностей
Теория случайных погрешностей была создана К.Ф.Гауссом в первой половине XIX в. в связи с его занятиями астрономией и геодезией.
Напомним, что случайные погрешности δi = xi — a проявляются при проведении серии измерений одной и той же физической величины в неизменных условиях одним и тем же методом.
Одним из фундаментальных положений теории Гаусса является «принцип арифметической середины». В соответствии с этим принципом за истинное значение величины а принимается среднее значение
при n → ∞, если метод не сопровождается систематическими погрешностями.
Для случайных погрешностей характерны следующие свойства:
- Положительные и отрицательные случайные погрешности встречаются с одинаковой вероятностью, т. е. одинаково часто.
- Среднее арифметическое из алгебраической суммы случайных погрешностей при неограниченном возрастании числа наблюдений стремится к нулю, т. е.
- Малые по абсолютной величине случайные погрешности встречаются с большей вероятностью, чем большие.
Основная идея теории Гаусса может быть выражена следующим образом
Возможные конкретные значения случайной погрешности, как и сам результат измерения, предсказать невозможно. Однако после того как экспериментатор определил измеряемый параметр и метод его измерения, сразу «возник» объективный закон, неизвестный исследователю. Этот закон определяет совокупность случайных погрешностей, которые возникают в процессе измерений.
Всегда можно эмпирически (на конкретных опытах) выявить закон распределения случайных погрешностей, который обычно выражается в виде так называемой функции распределения f(δ). Этот закон позволяет определить вероятность, с которой погрешность может оказаться в интервале от δ1 до δ2. Вероятность эта равна площади заштрихованной криволинейной трапеции, представленной на графике функции распределения.
Гауссу удалось определить универсальный закон распределения, которому подчиняется огромный класс случайных погрешностей измерений самых разных величин различными методами.
Этот закон носит название нормального закона распределения. Конечно, существуют измерения, погрешность которых не распределена по нормальному закону. Однако всегда можно определить степень их отклонения от нормального закона.
Функция распределения φ(δ), открытая Гауссом, имеет следующие свойства:
1) Функция δ(φ) четная, т. е. δ-(φ-)δ(φ), и в силу этого симметрична относительно оси координат.
2) Функция δ(φ) имеет максимум при значениях случайной погрешности, равных нулю.
3) Функция δ(φ) имеет две точки перегиба, расположенные симметрично относительно оси координат. Координаты точек перегиба равны ±σ.
4) Касательные к кривой δ(φ) в точках перегиба отсекают на оси абcцисс отрезки, равные ±2σ.
5) Максимальное значение функции δ(φ) равно
6) Площадь под всей кривой δ(φ) стремится к 1. Площадь криволинейной трапеции, ограниченной прямыми, проходящими через точки δ1,2 = ±σ, составляет 0,68 от всей площади; если прямые проходят через точки δ3,4 = ±2σ, то площадь составляет 0,95; площадь криволинейной трапеции, ограниченной прямыми δ5,6 = ±3σ, равна 0,99.
Параметр σ, определяющий все фундаментальные свойства нормального закона, называется средним квадратическим отклонением. Этот параметр может быть определен после получения достаточно большой серии результатов измерений x1, х2, х3, …, хn. Тогда
Важность параметра σ состоит в том, что он позволяет определить границы случайных погрешностей. Действительно, вероятность получения случайных погрешностей, превосходящих по абсолютной величине 3σ, равна 1%.
При обычной организации измерений не представляется возможности провести не только бесконечно большое число измерений, но и провести просто большое их число.
Специальные исследования показали, что такая граница может быть определена при небольшом числе опытов в серии.
В такой серии из k измерений находят так называемую среднюю квадратичную погрешность
Затем Δхкв увеличивают в S раз.
Число S называется коэффициентом Стьюдента (коэффициент был предложен в 1908 г. английским математиком В. С. Госсетом, публиковавшим свои работы под псевдонимом Стьюдент — студент). Коэффициент Стьюдента позволяет определить границу случайной погрешности серии: Δхслуч = S Δхкв.
Таблица коэффициентов S для различного числа опытов в серии
Погрешность среднего арифметического
После проведения серии равноточных измерений и нахождения хср и σ легко определяется интервал, к которому с вероятностью 99% принадлежит результат любого следующего измерения. Этот интервал равен [хср ± 3σ], если в серии достаточно много измерений, и имеет вид [хср ± S Δхкв] при небольшом числе опытов. Это означает, что 3σ (или S Δхкв) характеризует погрешность каждого опыта серии. Итак, среднее квадратичное отклонение серии опытов есть погрешность каждого опыта серии. Именно поэтому вводится обозначение σх или ΔSкв.х. Однако среднее арифметическое есть разумная комбинация всех измерений, и поэтому следует ожидать, что истинное значение находится в более узком интервале около хср, чем [xcp ± 3σх].
Понять, почему должно быть именно так, помогут следующие рассуждения
Выполняется N серий по n опытов в каждой. В каждой серии из n опытов определяется среднее значение хср. Таких средних значений получается N: хср1, хср2, …, xcpN. Для этой совокупности средних определяется среднее квадратичное отклонение
Погрешность среднего арифметического
После проведения серии равноточных измерений и нахождения хср и σ легко определяется интервал, к которому с вероятностью 99% принадлежит результат любого следующего измерения. Этот интервал равен [хср ± 3σ], если в серии достаточно много измерений, и имеет вид [хср ± S Δхкв] при небольшом числе опытов. Это означает, что 3σ (или S Δхкв) характеризует погрешность каждого опыта серии. Итак, среднее квадратичное отклонение серии опытов есть погрешность каждого опыта серии. Именно поэтому вводится обозначение σх или ΔSкв.х. Однако среднее арифметическое есть разумная комбинация всех измерений, и поэтому следует ожидать, что истинное значение находится в более узком интервале около хср, чем [xcp ± 3σх].
Понять, почему должно быть именно так, помогут следующие рассуждения
Выполняется N серий по n опытов в каждой. В каждой серии из n опытов определяется среднее значение хср. Таких средних значений получается N: хср1, хср2, …, xcpN. Для этой совокупности средних определяется среднее квадратичное отклонение
Величина σх ср характеризует предельное распределение средних значений, это и есть величина, которая позволяет найти интервал, в котором находится истинное значение измеряемой в опыте величины [хср ± 3σх ср]. На практике такая процедура никогда не реализуется не только потому, что это очень трудоемко, но и потому, что теория погрешностей позволяет по результатам одной серии определить погрешность среднего. Это делается на основе фундаментального результата теории погрешностей:
стандартное отклонение среднего σх ср в раз меньше стандартного отклонения каждого опыта серии σх, т.е.
раз меньше стандартного отклонения каждого опыта серии σх, т.е.
Итак, если в серии с достаточно большим числом опытов определено хср, то граница случайной погрешности среднего равна
Если в серии небольшое число опытов, то граница случайной погрешности среднего находится по формуле:
Все расчеты случайных погрешностей возможны только с использованием режима статистических расчетов (см. раздел «Статистические расчеты»), следуя методическим рекомендациям, приведенным ниже.
Использование калькулятора CASIO fx-82EX СLASSWIZ для оценки случайных погрешностей
- Включаем калькулятор, клавиша [ON]
- Нажимаем клавишу [SHIFT](SETUP)
- Входим в режим статистики. Нажимаем клавишу [2]
- Выбираем режим 1-Variable. Нажимаем клавишу [1]
- Заполняем таблицу
- Нажимаем клавишу [OPTN]
- Выбираем режим 1-Variable. Нажимаем клавишу [3]
- На дисплее получаем ряд характеристик
8.1. Первая сверху — значение среднего значенияВсе расчеты случайных погрешностей возможны только с использованием режима статистических расчетов (см. раздел «Статистические расчеты»), следуя методическим рекомендациям, приведенным ниже.
Использование калькулятора CASIO fx-82EX СLASSWIZ для оценки случайных погрешностей
- Включаем калькулятор, клавиша [ON]
- Нажимаем клавишу [SHIFT](SETUP)
- Входим в режим статистики. Нажимаем клавишу [2]
- Выбираем режим 1-Variable. Нажимаем клавишу [1]
- Заполняем таблицу
- Нажимаем клавишу [OPTN]
- Выбираем режим 1-Variable. Нажимаем клавишу [3]
- На дисплее получаем ряд характеристик
8.1. Первая сверху — значение среднего значения
8.2. Вторая снизу — случайная погрешность каждого опыта серии σх - Вычисляем погрешность среднего
- Находим границу случайной погрешности среднего
Пример
Измерялась скорость тела, брошенного горизонтально. В десяти опытах были получены следующие значения дальности полета L (в мм): 250, 245, 250, 262, 245, 248, 262, 260, 260, 248. Дальность полета тела измерялась линейкой с основной погрешностью Δ1 = 1мм. Высота, с которой брошено тело, в опыте равнялась Н = 1 м и измерялась мерной лентой с основной погрешностью Δ2 = 1 см и ценой деления С2 =1 см.
Решение
Сначала определим среднее значение дальности полета тела и вычислим его начальную скорость. Для этого сведем все данные в таблицу и проведем их первичную обработку.
Так как
Легко определить среднее значение скорости по результатам серии опытов:
Так как
Легко определить среднее значение скорости по результатам серии опытов:
Граница относительной погрешности измерения скорости:
В этой формуле ΔL — граница абсолютной погрешности измерения дальности полета, Δg — погрешность округления g, ΔН — погрешность прямого однократного измерения высоты.
ΔН = 1 см + 0,5 см = 1,5 см
ΔL складывается из погрешности линейки Δ1 и случайной погрешности ΔLслуч.:
ΔL = Δ1 + ΔLслуч.
Так как ΔLкв = 7мм, то при оценке ΔLслуч. нет смысла учитывать погрешность линейки Δ1 = 1мм.
Определим погрешность измерения скорости в любом однократном опыте, который можно провести на данной установке. В этом случае в формулу для εv следует вместо ∆L подставить его границу ∆L = S ∆Lкв. Здесь S = 3,2 (см. таблицу коэффициентов S для различного числа опытов в серии).
Имеем:
В этой формуле ΔL — граница абсолютной погрешности измерения дальности полета, Δg — погрешность округления g, ΔН — погрешность прямого однократного измерения высоты.
ΔН = 1 см + 0,5 см = 1,5 см
ΔL складывается из погрешности линейки Δ1 и случайной погрешности ΔLслуч.:
ΔL = Δ1 + ΔLслуч.
Так как ΔLкв = 7мм, то при оценке ΔLслуч. нет смысла учитывать погрешность линейки Δ1 = 1мм.
Определим погрешность измерения скорости в любом однократном опыте, который можно провести на данной установке. В этом случае в формулу для εv следует вместо ∆L подставить его границу ∆L = S ∆Lкв. Здесь S = 3,2 (см. таблицу коэффициентов S для различного числа опытов в серии).
Имеем:
Первое слагаемое в этой сумме равно 0,09; слагаемое в скобках (0,01 + 0,0075) = 0,0175. Следовательно, εv = 0,09. Граница абсолютной погрешности каждого опыта серии не превосходит
εv = ε0 = 0,565 ∙ 0,09 = 0,05 м/с
Это значит, если на данной установке провести еще один опыт, то гарантировать можно, что значение скорости, рассчитанное по его результатам, будет принадлежать интервалу [(0,56 — 0,05)м/с; (0,56 + 0,05)м/с].
Найдем границу случайной погрешности среднего значения скорости тела, брошенного горизонтально. Для этого в формулу для εv следует вместо ∆L подставить границу случайной погрешности среднего:
Таким образом,
Относительная погрешность среднего равна
0,027 + 0,01 + 0,0075
Последним слагаемым в этой сумме можно пренебречь. Итак, ср = 0,04 = 4%. Мы видим, что погрешность среднего в два раза меньше погрешности каждого опыта. Граница абсолютной погрешности среднего равна:
Таким образом, из серии 10 опытов по измерению скорости можно сделать вывод о том, что в любой другой такой серии из 10 опытов на данной установке среднее значение скорости будет находиться в интервале [(0,56 — 0,02)м/с; (0,56 + 0,02)м/с]. Этому же интервалу принадлежит неизвестное значение скорости, которое получится, если проделать серию с очень большим числом опытов, т. е. такое значение, которое можно назвать истинным значением.














