При прямых измеренияхзначение
измеряемой величины отсчитывается
непосредственно по шкале измерительного
прибора. Ошибка в отсчете может достигать
нескольких десятых долей деления шкалы.
Обычно при таких измерениях величину
систематической погрешности считают
равной половине цены деления шкалы
измерительного прибора. Например, при
измерении штангенциркулем с ценой
деления 0,05 мм величина приборной
погрешности измерения принимают равной
0,025 мм.
Цифровые измерительные приборы дают
значение измеряемых ими величин с
погрешностью, равной значению одной
единицы последнего разряда на шкале
прибора. Так, если цифровой вольтметр
показывает значение20,45 мВ, то абсолютная
погрешность при измерении равна
мВ.
Систематические погрешности возникают
и при использовании постоянных величин,
определяемых из таблиц. В подобных
случаях погрешность принимается равной
половине последнего значащего разряда.
Например, если в таблице значение
плотности стали дается величиной, равной
7,9∙103кг/м3, то абсолютная
погрешность в этом случае равнакг/м3.
Некоторые особенности в расчете приборных
погрешностей электроизмерительных
приборов будут рассмотрены ниже.
При определении систематической
(приборной) погрешности косвенных
измеренийфункциональной величиныиспользуется
формула
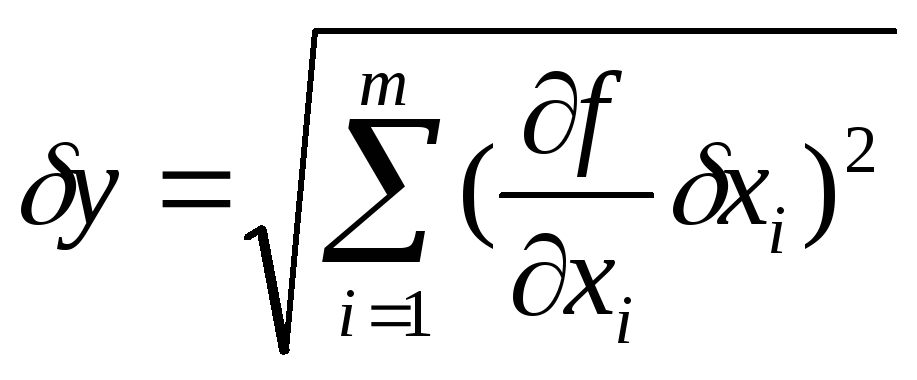
(1)
где
— приборные ошибки прямых измерений
величины,
—
частные производные функции по переменной.
В качестве примера, получим формулу для
расчета систематической погрешности
при измерении объема цилиндра. Формула
вычисления объема цилиндра имеет вид
.
Частные производные по переменным d
и hбудут равны
,
.
Таким образом, формула для определения
абсолютной систематической погрешности
при измерении объема цилиндра в
соответствии с (2. ..) имеет следующий вид
,
где
и
приборные
ошибки при измерении диаметра и высоты
цилиндра
3. Оценка случайной погрешности. Доверительный интервал и доверительная вероятность
Д
Рис. 1
ля подавляющего большинства простых
измерений достаточно хорошо выполняется
так называемый нормальный закон случайных
погрешностей (закон Гаусса), выведенный
из следующих эмпирических положений.
-
погрешности измерений могут принимать
непрерывный ряд значений; -
при большом числе измерений погрешности
одинаковой величины, но разного знака
встречаются одинаково часто, -
чем больше величина случайной погрешности,
тем меньше вероятность ее появления.
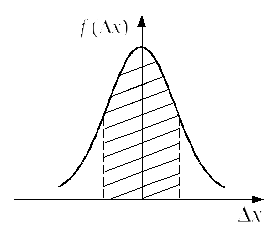
График нормального закона распределения
Гаусса представлен на рис.1. Уравнение
кривой имеет вид
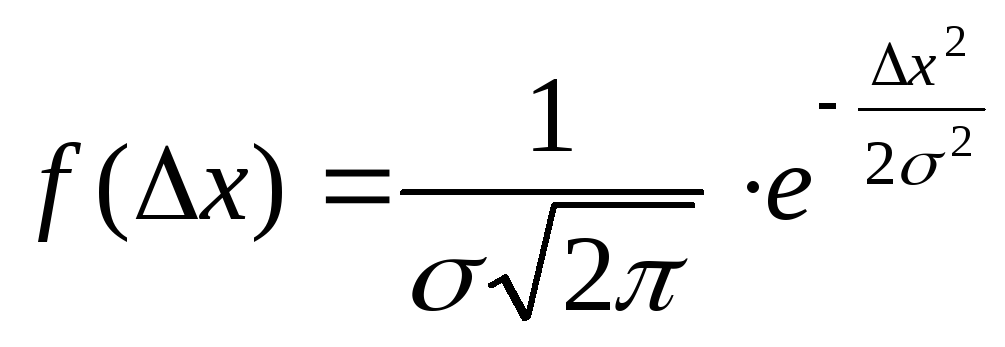
(2)
где
— функция распределения случайных ошибок
(погрешностей), характеризующая
вероятность появления ошибки,σ– средняя
квадратичная ошибка.
Величина σне
является случайной величиной и
характеризует процесс измерений. Если
условия измерений не изменяются, то σ
остается постоянной величиной. Квадрат
этой величины называютдисперсией
измерений.Чем меньше дисперсия, тем
меньше разброс отдельных значений и
тем выше точность измерений.
Точное значение средней квадратичной
ошибки σ, как
и истинное значение измеряемой величины,
неизвестно. Существует так называемая
статистическая оценка этого параметра,
в соответствии с которой средняя
квадратичная ошибка равняется средней
квадратичной ошибке среднего
арифметического.
Величина которой определяется по формуле

(3)
где
— результатi-го
измерения;—
среднее арифметическое полученных
значений;n – число
измерений.
Чем больше число измерений, тем меньше
и тем больше оно приближается кσ.
Если истинное значение измеряемой
величины μ, ее среднее арифметическое
значение, полученное в результате
измерений ,
а случайная абсолютная погрешность,
то результат измерений запишется в виде.
Интервал значений от
до
,
в который попадает истинное значение
измеряемой величины μ, называетсядоверительным интервалом.Посколькуявляется случайной величиной, то истинное
значение попадает в доверительный
интервал с вероятностью α, которая
называетсядоверительной вероятностью,илинадежностью измерений. Эта
величина численно равна площади
заштрихованной криволинейной трапеции.
(см. рис.)
Все это справедливо для достаточно
большого числа измерений, когда
близка к σ. Для отыскания доверительного
интервала и доверительной вероятности
при небольшом числе измерений, с которым
мы имеем дело в ходе выполнения
лабораторных работ, используетсяраспределение вероятностей Стьюдента.
Это распределение вероятностей
случайной величины,
называемойкоэффициентом Стьюдента,
дает значение доверительного интервалав долях средней квадратичной ошибки
среднего арифметического.
.
(4)
Распределение вероятностей этой величины
не зависит от σ2, а существенно
зависит от числа опытовn.С увеличением числа опытовnраспределение
Стьюдента стремится к распределению
Гаусса.
Функция распределения табулирована
(табл.1). Значение коэффициента Стьюдента
находится на пересечении строки,
соответствующей числу измерений n,
и столбца, соответствующего доверительной
вероятности α
Таблица 1.
|
n |
α |
n |
α |
||||||
|
0,8 |
0,9 |
0,95 |
0,98 |
0,8 |
0,9 |
0,95 |
0,98 |
||
|
3 |
1,9 |
2,9 |
4,3 |
7,0 |
6 |
1,5 |
2,0 |
2,6 |
3,4 |
|
4 |
1,6 |
2,4 |
3,2 |
4,5 |
7 |
1,4 |
1,9 |
2,4 |
3,1 |
|
5 |
1,5 |
2,1 |
2,8 |
3,7 |
8 |
1,4 |
1,9 |
2,4 |
3,9 |
Пользуясь данными таблицы, можно:
-
определить доверительный интервал,
задаваясь определенной вероятностью; -
выбрать доверительный интервал и
определить доверительную вероятность.
При косвенных измерениях среднюю
квадратичную ошибку среднего
арифметического значения функции
вычисляют по формуле
.
(5)
Доверительный интервал и доверительная
вероятность определяются так же, как и
в случае прямых измерений.
Оценка суммарной погрешности измерений.
Запись окончательного результата.
Суммарную погрешность результата
измерений величины Х будем определять
как среднее квадратичное значение
систематической и случайной погрешностей
,
(6)
где δх – приборная погрешность, Δх
– случайная погрешность.
В качестве Х может быть как непосредственно,
так и косвенно измеряемая величина.
Окончательный результат измерений
рекомендуется представлять в следующем
виде
,
α=…, Е=…(7)
Следует иметь в виду, что сами формулы
теории ошибок справедливы для большого
число измерений. Поэтому значение
случайной, а следовательно, и суммарной
погрешности определяется при малом nс большой ошибкой. При вычислении Δхпри числе измеренийрекомендуется
ограничиваться одной значащей цифрой,
если она больше 3 и двумя, если первая
значащая цифра меньше 3. Например, если
Δх= 0,042, то отбрасываем 2 и пишем
Δх=0,04, а если Δх=0,123, то пишем
Δх=0,12.
Число разрядов результата и суммарной
погрешности должно быть одинаковым.
Поэтому среднее арифметическое
погрешности должно быть одинаковым.
Поэтому среднее арифметическое
вычисляется вначале на один разряд
больше, чем измерение, а при записи
результата его значение уточняется до
числа разрядов суммарной ошибки.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Абсолютная погрешность
- Причины возникновения погрешности измерения
- Систематическая и случайная погрешности
- Определение абсолютной погрешности
- Алгоритм оценки абсолютной погрешности в серии прямых измерений
- Значащие цифры и правила округления результатов измерений
- Примеры
Причины возникновения погрешности измерения
Погрешность измерения – это отклонение измеренного значения величины от её истинного (действительного) значения.
Обычно «истинное» значение неизвестно, и можно только оценить погрешность, приняв в качестве «истинного» среднее значение, полученное в серии измерений. Таким образом, процесс оценки проводится статистическими методами.
Виды погрешности измерений
Причины
Инструментальная погрешность
Определяется погрешностью инструментов и приборов, используемых для измерений (принципом действия, точностью шкалы и т.п.)
Погрешность метода
Определяется несовершенством методов и допущениями в методике.
Теоретическая погрешность
Определяется теоретическими упрощениями, степенью соответствия теоретической модели и реальности.
Погрешность оператора
Определяется субъективным фактором, ошибками экспериментатора.
Систематическая и случайная погрешности
Систематической погрешностью называют погрешность, которая остаётся постоянной или изменяется закономерно во времени при повторных измерениях одной и той же величины.
Систематическая погрешность всегда имеет знак «+» или «-», т.е. говорят о систематическом завышении или занижении результатов измерений.
Систематическую погрешность можно легко определить, если известно эталонное (табличное) значение измеряемой величины. Для других случаев разработаны эффективные статистические методы выявления систематических погрешностей. Причиной систематической погрешности может быть неправильная настройка приборов или неправильная оценка параметров (завышенная или заниженная) в расчётных формулах.
Случайной погрешностью называют погрешность, которая не имеет постоянного значения при повторных измерениях одной и той же величины.
Случайные погрешности неизбежны и всегда присутствуют при измерениях.
Определение абсолютной погрешности
Абсолютная погрешность измерения – это модуль разности между измеренным и истинным значением измеряемой величины:
$$ Delta x = |x_{изм}-x_{ист} | $$
Например:
При пяти взвешиваниях гири с маркировкой 100 г были получены различные значения массы. Если принять маркировку за истинное значение, то получаем следующие значения абсолютной погрешности:
$m_i,г$
98,4
99,2
98,1
100,3
98,5
$Delta m_i, г$
1,6
0,8
1,9
0,3
1,5
Граница абсолютной погрешности – это величина h: $ |x-x_{ист}| le h $
Для оценки границы абсолютной погрешности на практике используются статистические методы.
Алгоритм оценки абсолютной погрешности в серии прямых измерений
Шаг 1. Проводим серию из N измерений, в каждом из которых получаем значение измеряемой величины $x_i, i = overline{1, N}$.
Шаг 2. Находим оценку истинного значения x как среднее арифметическое данной серии измерений:
$$ a = x_{cp} = frac{x_1+x_2+ cdots +x_N}{N} = frac{1}{N} sum_{i = 1}^N x_i $$
Шаг 3. Рассчитываем абсолютные погрешности для каждого измерения:
$$ Delta x_i = |x_i-a| $$
Шаг 4. Находим среднее арифметическое абсолютных погрешностей:
$$ Delta x_{cp} = frac{Delta x_1+ Delta x_2+ cdots + Delta x_N}{N} = frac{1}{N} sum_{i = 1}^N Delta x_i $$
Шаг 5. Определяем инструментальную погрешность при измерении как цену деления прибора (инструмента) d.
Шаг 6. Проводим оценку границы абсолютной погрешности серии измерений, выбирая большую из двух величин:
$$ h = max {d; Delta x_{cp} } $$
Шаг 7. Округляем и записываем результаты измерений в виде:
$$ a-h le x le a+h или x = a pm h $$
Значащие цифры и правила округления результатов измерений
Значащими цифрами – называют все верные цифры числа, кроме нулей слева. Результаты измерений записывают только значащими цифрами.
Например:
0,00501 — три значащие цифры 5,0 и 1.
5,01 — три значащие цифры.
5,0100 – пять значащих цифр; такая запись означает, что величина измерена с точностью 0,0001.
Внимание!
Правила округления.
Погрешность измерения округляют до первой значащей цифры, всегда увеличивая ее на единицу (округление по избытку, “ceiling”).
Округлять результаты измерений и вычислений нужно так, чтобы последняя значащая цифра находилась в том же десятичном разряде, что и абсолютная погрешность измеряемой величины.
Например: если при расчетах по результатам серии измерений получена оценка истинного значения a=1,725, а оценка абсолютной погрешности h = 0,11, то результат записывается так:
$$ a approx 1,7; h approx ↑0,2; 1,5 le x le 1,9 или x = 1,7 pm 0,2 $$
Примеры
Пример 1. При измерении температура воды оказалась в пределах от 11,55 ℃ до 11,63 ℃. Какова абсолютная погрешность этих измерений?
По условию $11,55 le t le 11,63$. Получаем систему уравнений:
$$ {left{ begin{array}{c} a-h = 11,55 \ a+h = 11,63 end{array} right.} Rightarrow {left{ begin{array}{c} 2a = 11,55+11,63 = 23,18 \ 2h = 11,63-11,55 = 0,08 end{array} right.} Rightarrow {left{ begin{array}{c} a = 11,59 \ h = 0,04end{array} right.} $$
$$ t = 11,59 pm 0,04 ℃ $$
Ответ: 0,04 ℃
Пример 2. По результатам измерений найдите границы измеряемой величины. Инструментальная погрешность d = 0,1.
$x_i$
15,3
16,4
15,3
15,8
15,7
16,2
15,9
Находим среднее арифметическое:
$$ a = x_{ср} = frac{15,3+16,4+ cdots +15,9}{7} = 15,8 $$
Находим абсолютные погрешности:
$$ Delta x_i = |x_i-a| $$
$ Delta x_i$
0,5
0,6
0,5
0
0,1
0,4
0,1
Находим среднее арифметическое:
$$ Delta x_{ср} = frac{0,5+0,6+ cdots + 0,1}{7} approx 0,31 gt d $$
Выбираем большую величину:
$$ h = max {d; Delta x_{ср} } = max {0,1; 0,31} = 0,31 $$
Округляем по правилам округления по избытку: $h approx ↑0,4$.
Получаем: x = 15, $8 pm 0,4$
Границы: $15,4 le x le 16,2$
Ответ: $15,4 le x le 16,2$
Пример 3*. В первой серии экспериментов было получено значение $x = a pm 0,3$. Во второй серии экспериментов было получено более точное значение $x = 5,631 pm 0,001$. Найдите оценку средней a согласно полученным значениям x.
Более точное значение определяет более узкий интервал для x. По условию:
$$ {left{ begin{array}{c} a-0,3 le x le a+0,3 \ 5,630 le x le 5,632 end{array} right.} Rightarrow a-0,3 le 5,630 le x le 5,632 le a+0,3 Rightarrow $$
$$ Rightarrow {left{ begin{array}{c} a-0,3 le 5,630 \ 5,632 le a+0,3 end{array} right.} Rightarrow {left{ begin{array}{c} a le 5,930 \ 5,332 le a end{array} right.} Rightarrow 5,332 le a le 5,930 $$
Т.к. a получено в серии экспериментов с погрешностью h=0,3, следует округлить полученные границы до десятых:
$$ 5,3 le a le 5,9 $$
Ответ: $ 5,3 le a le 5,9 $
Разница между случайной и систематической ошибкой
Если ошибка не имеет какой-либо конкретной модели возникновения, она известна как случайная ошибка, которая также известна как несистематическая ошибка, и, следовательно, такие ошибки нельзя предсказать заранее, как неизбежную ошибку, тогда как систематическая ошибка — это ошибка, которая может возникнуть. из-за любой ошибки в измерении прибора ошибка или ошибка в использовании прибора экспериментатором и, следовательно, это ошибка, которой можно избежать.
Основное отличие состоит в том, что случайные ошибки в основном приводят к колебаниям, которые окружают истинное значение из-за трудностей при проведении измерений, тогда как систематические ошибки приводят к предсказуемым, а также постоянным отклонениям от истинного значения из-за проблем с калибровка оборудования.
Независимо от того, насколько осторожны при проведении экспериментов, скорее всего, будет ошибка, называемая экспериментальной ошибкой. Будь то из-за присущих ему проблем, связанных с проблемами с вашим оборудованием, точным выполнением измерений или полным предотвращением ошибки, это практически невозможно.
Чтобы противостоять упомянутой проблеме, ученые стараются изо всех сил классифицировать эти ошибки и пытаться количественно оценить любую неопределенность в измерениях, которые они делают. Выявление разницы между этими ошибками является жизненно важной частью обучения, позволяющего разрабатывать более эффективные эксперименты и пытаться свести к минимуму любые ошибки, которые действительно подкрадываются.
Инфографика случайных и систематических ошибок
Давайте посмотрим основные различия между случайной ошибкой и систематической ошибкой.
Ключевые отличия
Ключевые отличия заключаются в следующем:
- Случайная ошибка определяет себя как непредсказуемое нарушение, которое возникает в вашем эксперименте из-за неизвестного источника. При этом систематическая ошибка возникает из-за неисправности аппарата, который не построен.
- Случайная ошибка, как указано в приведенной выше таблице, возникает в обоих направлениях, тогда как систематическая ошибка возникает только в одном направлении. Систематические ошибки возникают из-за встроенной неисправности или ошибки аппарата; следовательно, он всегда дает аналогичную ошибку. Случайная ошибка, как упоминалось ранее, возникает из-за неизвестного источника, поэтому она возникает в любом направлении.
- Величина систематической ошибки будет оставаться постоянной или неизменной, потому что дефект, который присутствует в ней, встроен внутри устройства, и по сравнению с величиной случайной ошибки он имеет переменную величину.
- Ошибка 0 и неправильная калибровка прибора вызовут систематическую ошибку. Случайная ошибка возникает из-за параллакса или, как указано ранее в приведенной выше сравнительной таблице, из-за неправильного использования устройства.
- Случайная погрешность уменьшается или может быть минимизирована путем получения 2 или более показаний одного и того же эксперимента, в то время как систематическая ошибка может быть минимизирована путем тщательного проектирования конструкции устройства.
- Случайная ошибка сама по себе уникальна и не имеет конкретных типов, тогда как систематическая ошибка может быть разделена на три основных типа: ошибка среды, ошибка прибора и систематическая ошибка.
- Случайная ошибка не воспроизводится, с другой стороны, систематическая ошибка будет воспроизводимой, потому что дефект, как указано ранее, встроен в структуру устройства.
Сравнительная таблица случайных и систематических ошибок
| Основа | Случайная ошибка | Систематическая ошибка | ||
| Основное определение | Это ошибки, которые колеблются из-за неопределенности или непредсказуемости, присущей вашему процессу измерения, или различий в величине, которую вы пытаетесь измерить. | Это происходит в основном из-за недостатков оборудования, то есть они обычно возникают из-за неправильной калибровки оборудования. | ||
| Величина ошибки | Величина ошибки меняется при каждом чтении. | Измеренное значение будет либо очень низким, либо очень высоким по сравнению с истинным значением. | ||
| Причины | 1) Ошибка параллакса
2) Неправильное использование аппарата. 3) Ограничение инструмента, среды и т. Д. |
1) Нулевая ошибка
2) Неправильная калибровка |
||
| Методы минимизации | Повторно снимая показания. | 1) За счет улучшения конструкции аппарата.
2) Ошибка нуля может быть уменьшена путем вычитания из ошибки нуля полученного показания. |
||
| Направление ошибки | Это происходит с обеих сторон | Это происходит только в одном направлении. | ||
| Подтипы ошибок | Подтипов нет. | Есть 3 подтипа — a. Инструмент b. Систематическая ошибка c. Среда. | ||
| Воспроизводимо ли это | Этот вид ошибки не воспроизводится | Этот вид ошибки воспроизводится | ||
| С точки зрения стоимости | Цена — это комбинация стоимости, которая в основном связана с производством. | Затраты снижаются, когда они сравниваются со стоимостью с точки зрения стоимости. |
Вывод
Случайная ошибка в основном возникает из-за каких-либо нарушений, происходящих в вашем окружении, таких как колебания или перепады давления, температуры или из-за наблюдателя, который может принимать неправильные или неправильные показания. Систематическая ошибка, возможно, также возникает из-за механической конструкции аппарата.
Случайных ошибок по существу нельзя избежать, а систематических ошибок можно избежать. Ученые не могут делать точных масштабов или измерений, какими бы умелыми они ни были.
Систематические ошибки, возможно, трудно обнаружить, и это связано с тем, что все, что вы измеряете, будет неверным или неверным на ту же величину, и вы, возможно, вообще не осознаете, что существует проблема. Перед использованием необходимо правильно откалибровать оборудование, и да, тогда вероятность систематических ошибок будет намного меньше.