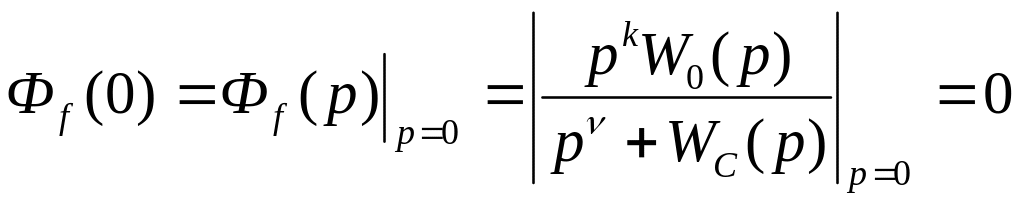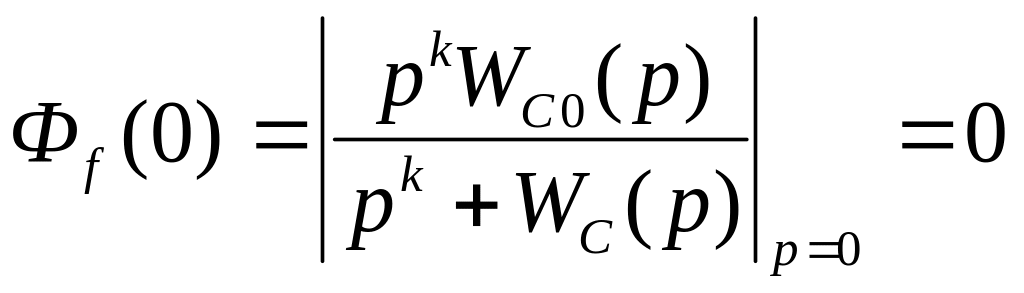Оценка качества регулирования в установившемся режиме коэффициенты ошибок - Oshibki.top

Статические
и астатические системы.

В САР могут быть
звенья, у которых нет установившихся
соотношений между входными и выходными
величинами. Такие звенья не имеют
статической характеристики и называются
астатическими(интегрирующее звено).
При этом следует отметить, что в
астатических звеньях в установившихся
режимах существуют однозначные
зависимости производных выходной
величины от различных постоянных
значений входной величины. Как было
показано ПФ-я остаточной системы может
быть представлена в виде:

(1)

—
порядок астатизма,

— ПФ статической части системы(без
интегрирующих звеньев). При

(система является статической), иногда
говорят, что она обладает астатизмом
«0»- го порядка. Рассмотрим САР, состоящую
из ОР с ПФ

и регулятора с ПФ

(рис. 16)

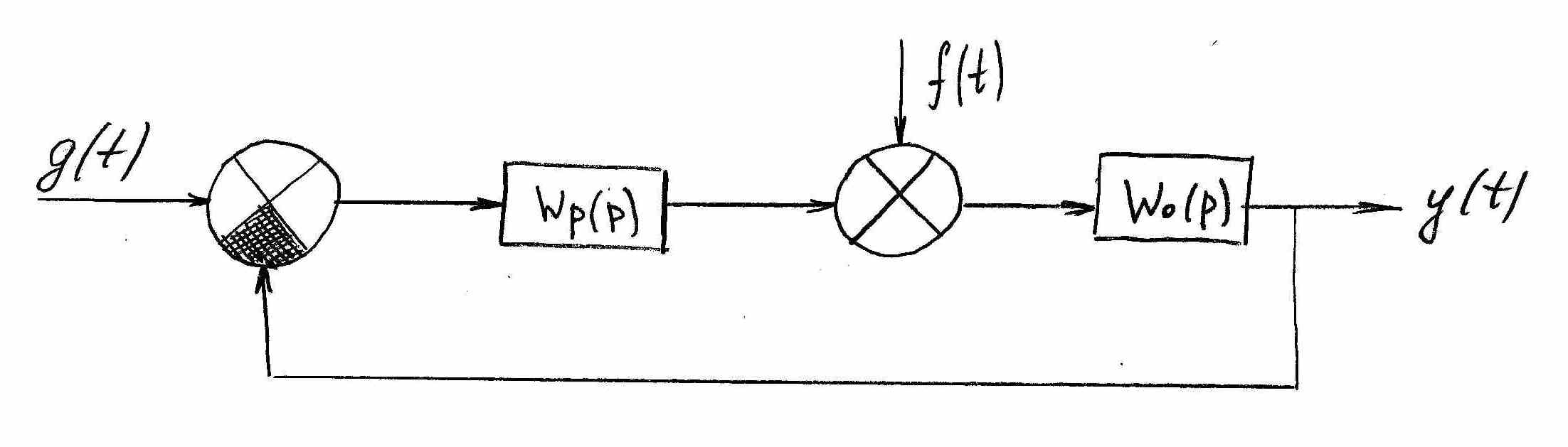
Рисунок 16

;
(*)

ОР и регуляторы,
которые могут быть представлены в виде
астатического звена или соединения,
называются астатическими, иные они
называются статическими. Иногда
астатические объекты называются
объектами без самовыравнивания,
статические – с самовыравниванием.
Физически
эти названия объясняются тем, что в
астатических объектах при поступлении
на их входы постоянного по величине
воздействия значение регулируемой(выходной)
величины теоретически возрастает до
бесконечности (интегрирующего звена

).
В статических
объектах при аналогичном условии
выходная величина увеличивается только
до некоторого постоянного значения,
т.е. происходит стабилизация(самовыравнивание)
выходной величины на новом уровне,
который осуществляется самим объектом
даже при отсутствии регулятора
(апериодическое звено 1-го порядка). Так
как САР имеет различные структурные
схемы относительно задающего и возмущающих
воздействий, то с точки зрения статизма
и астатизма их необходимо оценивать
относительно этих воздействий раздельно.

В установившихся
режимах оценка качества регулирования
проводится по величине установившейся
ошибки (*).Чем меньше ошибка, тем выше
качество системы при влиянии на систему
задающего и возмущающего воздействий:

,
(2)

где

и

.

В соответствии с
(1) ПФ объекта и регулятора:

где e,k
– порядки астатизма объекта и регулятора;

— ПФ статической части объекта и
регулятора. Тогда
ПФ замкнутой системы по ошибке:

где

—
порядок астатизма системы;

_.

_{ПФ замкнутой

системы по возмущению:}

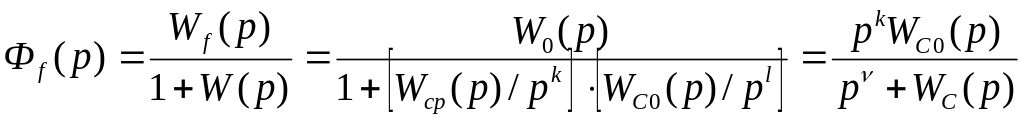
_{Определение

установившихся ошибок при различных

воздействий:}

_{А) оба воздействия

являются ступенчатыми функциями.}

,

,
;

,
,
;

Установившаяся
ошибка возникающая при этих воздействиях
называют статической ошибкой, то есть

В этом случае согласно
формуле (2):

;

Следовательно,
установившаяся ошибка вызвана тем или
иным воздействием зависит не только от
величины этого воздействия, но и от
начального значения соотношений ПФ, то
есть при

.

Если

,
то

и система является астатической по
каналу возмущающего воздействия. Если

,
то

система является астатической по каналу
возмущающего воздействия. Если

или

,
то система является статической по
соответствующему каналу.

Рассмотрим
следующие 4 случая:

Регулятор
астатический (
)
, объект астатический (
)
,

,
тогда

;

,
то есть система является статической
по обоим каналам.

Регулятор
астатический(

)
,объект статический (

),

,тогда

;

Система по обоим
каналам является астатической.

Регулятор
статический (
),
объект астатический (

),

,
тогда

;

,
где

,

— коэффициенты передачи объекта и
регулятора.

Таким образом,
система является астатической по каналу
задающего воздействия и статической
по каналу возмущающего воздействия.

Объект
и регулятор статические (
),
тогда

;

Составляющая
ошибки

практически всегда может быть сведена
к 0 за счет использования неединичной
ОС. Она равна
нулю в системе автоматической стабилизации,
у которой

.

Относительное
значение установившейся ошибки называется
коэффициентом статизма системы по
соответствующему каналу.

— коэффициент
статизма системы по задающему воздействию;

— коэффициент
статизма системы по возмущающему
воздействию.

Таким
образом система с единичной ОС является
статической по обоим каналам.

Полученные результаты представляются
в виде таблицы.

№	Регулятор	Объект
1	А	А	А	А
2	А	С	А	А
3	С	А	А	С
4	С	С	С	С

Выводы:

Если
регулятор астатический, то независимо
от ОР система по обоим каналам
астатическая.
Если
регулятор статический, то независимо
от ОР система статическая по каналу
возмущающего воздействия. Астатизм по
каналу задающего воздействия определяется
астатизмом объекта.

Б) Задающее воздействие
имеет вид линейной функции

,
где

—
скорость изменения задающего воздействия

Преобразуя по
Лапласу, имеем:

,

,
тогда

Такой режим применяется
в следящих системах. Очевидно,
что составляющая

имеет смысл только для системы с
астатизмом 1-го порядка, то есть

.

В
этом случае она называется скоростной
ошибкой или ошибкой по скорости ,т.к
пропорциональна скорости изменения
задающего воздействия.

,где К=

— коэф-т передачи разомкнутой системы
назв. добротностью системы по скорости.

Ошибка
по скорости свидетельствует о том, что
в установившемся режиме выходная
величина будет изменяться со скоростью
равной скорости изменения задающего
воздействия, но с некоторым отставанием
во времени.

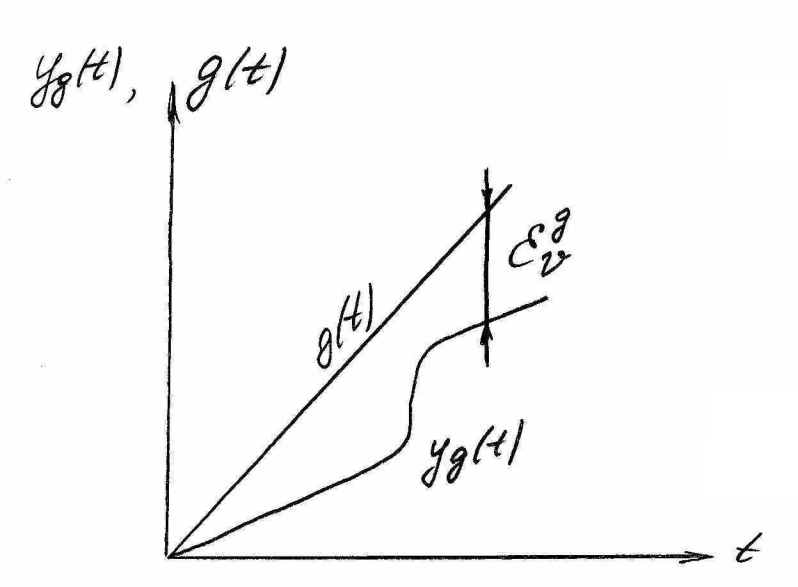
Чем
больше добротность системы по скорости
,тем меньше будет отставать система при
отростке входного воздействия. ,тем
выше качество системы .В статической
системе ,при астатизме

=0
.

Вторая
составляющая ошибки

представляет собой статическую ошибку
,т.к f(t)=
=const

Т.о
в этом типовом режиме

В)
Задающее воздействие имеет вид
квадратичной функции:

,
где

а
=const – ускорение изменения
задающего воздействия F(t)=

1(t)
. Преобразуя по Лапласу
.

Этот
режим имеет смысл только для следящих
систем и систем программного регулирования,
обладающих астатизмом

>1.В этом случае

Это
составляющая имеет смысл с =1 в этом
случае оте назв. ошибкой по ускорению
.

К=

— добротность по ускорению,

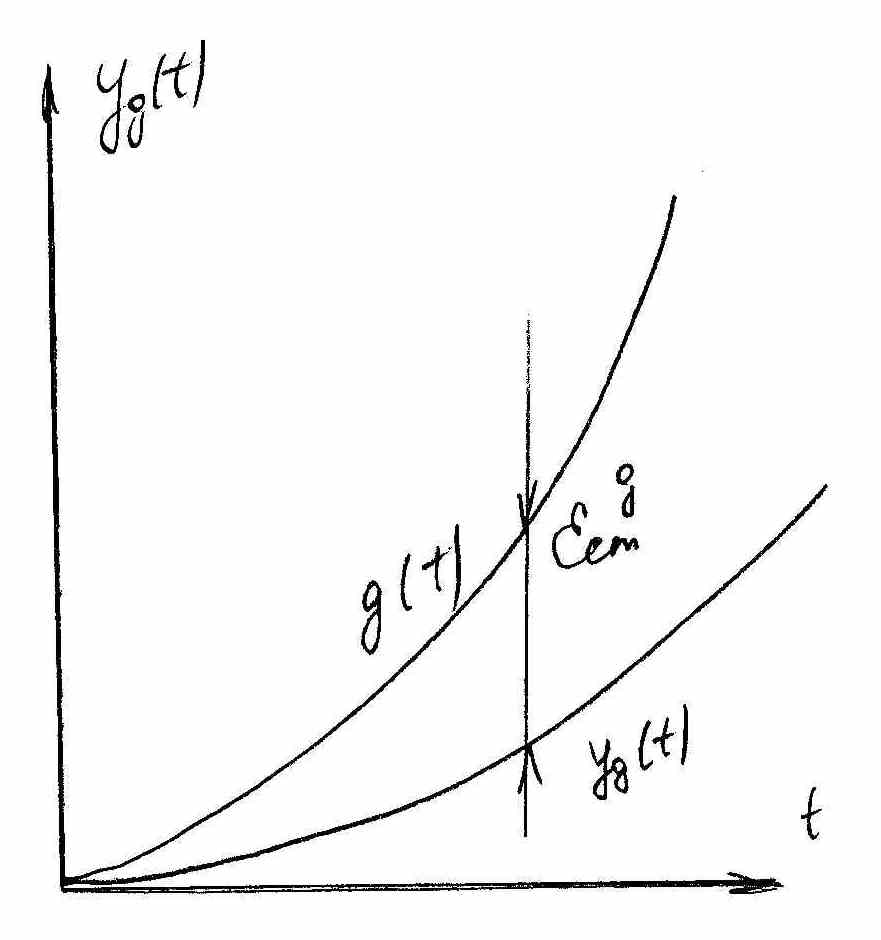
Чем
выше

,тем лучше качество САР.В этом типовом
режиме установившееся ошибка
.

С
помощью теоремы о конечном значении
легко показать ,что в системе с =2
статическая скоростная ошибка от
задающего воздействия=0.

Г)
Задающее воздействие имеет вид
синусоидальной функции.

G(t)=Gmax*
sinwgt

Возмущающее
воздействие изменятся в этом режиме
,либо оставаться постоянным. Рассмотрим
ошибку только от задающего воздействия
,тогда её изображение

(3)

Очевидно
,что в установившемся режиме ошибка
будет также изменятся по синусоидальному
закону с той же частотой

Eуст(t)=Emax
sinn(wgt+ф)

В
этом режиме точность системы обычно
оценивается по амплитуде ошибки, которая
может быть найдена из (3) путем подстановки

P=jwg

Обычно
Gmax

Emax
поэтому модуль знаменателя больше 1 , а
следовательно с большей точностью
можно принять , что

, где

A(wg)-АЧХ
разомкнутой системы.

Из
этого уравнения следует требования и
АЧХ разомкнутой системы ,при достигается
требуемая точность регулирования.

или 20lgA(wg)=L(wg)

20lgGmax/Emax

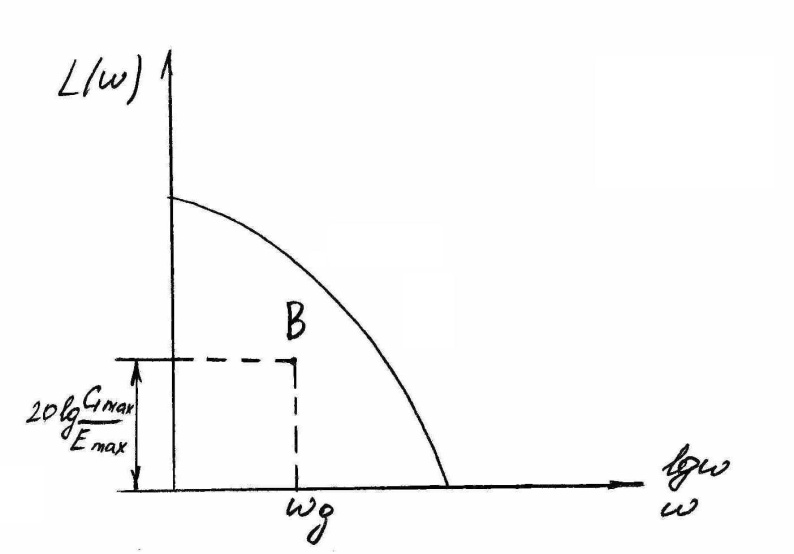
Последнее
выражение ограничивает местоположение.
ЛАХ около точки .Требования по точности.

Д)
Задающее воздействие имеет вид
произвольной функции .Если g(t)
имеет произвольную , то достаточно
плавную форму изменения, то для оценки
точности системы в установившемся
режиме существенное значение имеет
лишь конечное число n-производных

Установившееся
ошибка при задающем воздействии g(t)
может быть определена с помощью интеграла
свертки. Eуст(t)=

,где

-весовая функция ошибки. Преобразуем
это выражение .Для этого разложим функцию
g(t-r)
на интервале от 0 до в ряд Тейлора

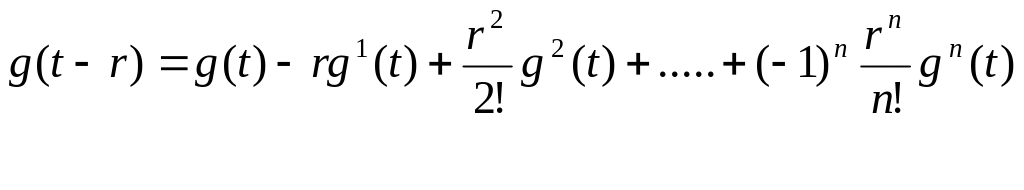
Подставляя
это выражение в формулу свертки будем
иметь

Eуст(t)=

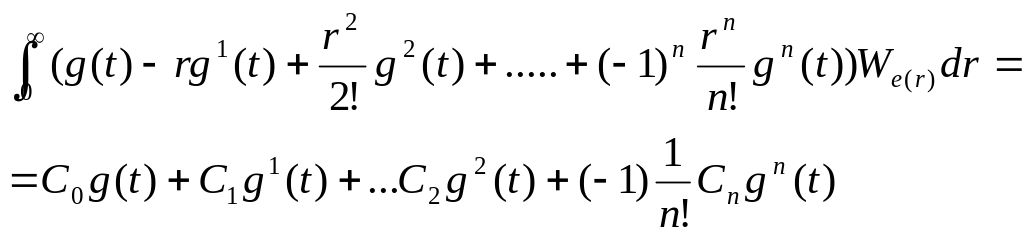
,где

Коэффициенты
определяющие величину ошибки назв.
коэффициентами ошибок. Эти коэф-ты
могут быть найден только с помощью
выражения (3) и с помощью ПФ-и ошибки.

(6)

Из
операционного исчисления известно ,
что условие P=0 соот-т времени t= ,т.е
установившемуся значению функции
времени .Полагая в уравнение (6) р=0 находим
коэффициент ошибки .

Продифференцировав
уравнение (6) по переменной р n-раз и
положив р=0 получим следующие коэффициенты
ошибок.

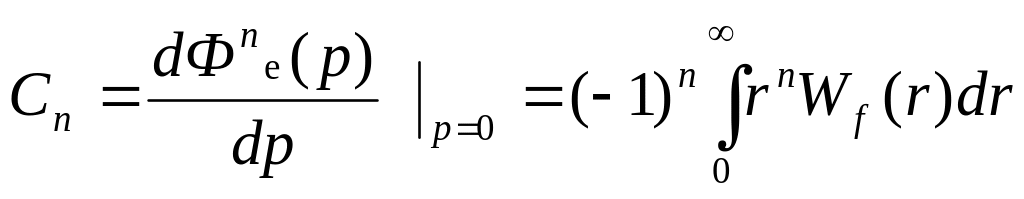
Преобразуя
уравнение (4) при нулевых начальных
условиях получим ,изображение ошибки.

Выражение
(7) представляет собой разложение функции
в ряд Макларена.

Учитывая,
что ПФ ошибки представляет собой
дробно-рациональную функцию

,то
коэф-ты ошибок можно определить путем
деления числителя N(р) на полином
знаменателя D( р) и сравнения получающегося
ряда с выражением (7).

Выше
было показано, что ПФ ошибки может быть
представлена в виде

.Тогда
для статических систем(

=0) ПФ ошибки

коэф-т ошибки .Т.о коэф-т определяет
астатизм системы ,а следовательно
статическую ошибку
.

выше систем с астатизмом 1-го порядка

Т.о
коэф-т хар-т ошибку системы по скорости.

Для
астатических систем 2-го порядка

,откуда

-характеризует
ошибку по ускорению.

Т.о
повышение порядка астатизма соответствует
повышению точности САР.

Сравним
точности статической и астатической
систем.Пусть на вход систем поступает
сигнал

, тогда установившееся ошибка будет
определятся :для статической систем
.

Для
астатической системы 1-го порядка

Для
системы с астатизмом 2-го порядка

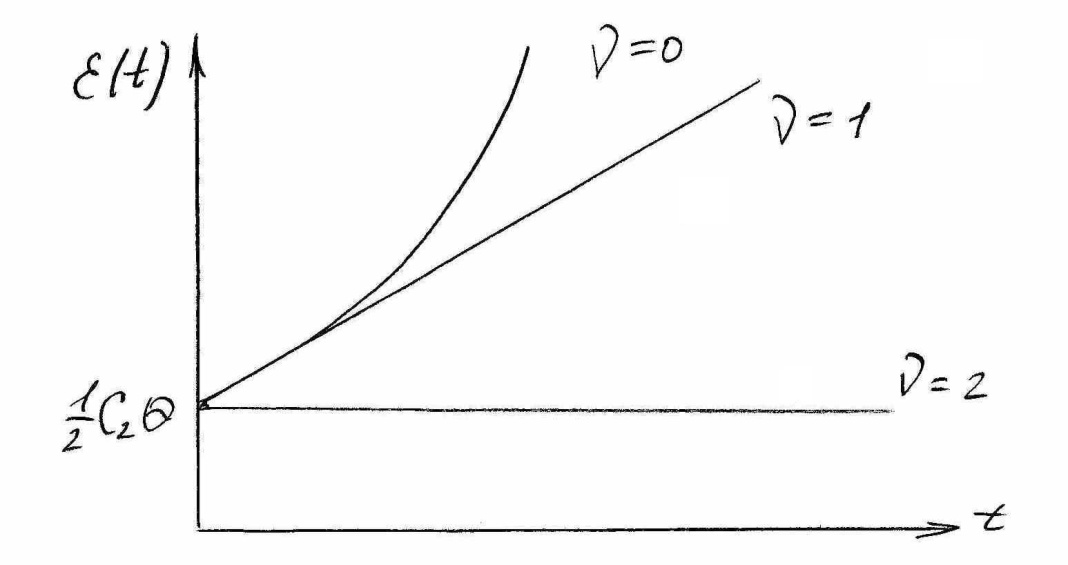
Рисунок 19

Как
видно из рисунка 19 положительную
точность имеет САР с астатизмом 2-го
порядка.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Макеты страниц

где коэффициенты принято называть коэффициентами ошибок. Формула (4.3) получена следующим образом.

Передаточная функция замкнутой системы относительно ошибки (рис. 4.1)

Из (4.4) можно найти выражение для изображения ошибки:

Разложим передаточную функцию по ошибке в ряд по возрастающим степеням s в окрестности точки что соответствует большим значениям времени т. е. значению установившейся ошибки при заданном управляющем воздействии.

В соответствии с (4.5) можно записать

Если передаточная функция является дробно-рациональной функцией

то разложение в ряд можно осуществить делением числителя на знаменатель, располагая члены полинома в порядке возрастания степеней. Переходя в (4.6) от изображений к оригиналам, можно получить для выражение (4.3).

Коэффициенты ошибок определяют по формулам разложения функции в ряд Тейлора:

Если то все производные тогда

В данном случае — значение установившейся ошибки в замкнутой системе.

Если ; коэффициенты и т. д.

Коэффициент называют коэффициентом статической или позиционной ошибки; коэффициент С — коэффициентом скоростной ошибки, — коэффициентом ошибки от ускорения.

В статических системах коэффициент отличен от нуля. В системах с астатизмом первого порядка . В системах с астатизмом второго порядка . Увеличение числа интегрирующих звеньев приводит к повышению порядка астатизма системы, т. е. к нулевым значениям нескольких коэффициентов ошибок, но при этом усложняется обеспечение устойчивости системы. Если на систему помимо задающего воздействия действует и возмущение (рис. 4.2), то астатизм системы относительно зависит от места включения интегрирующего звена.

Пусть воздействия на САУ являются постоянными величинами и равны Рассмотрим несколько случаев.

1. В системе отсутствуют интегрирующие звенья. Элементы 1 и 2 системы (рис. 4.2) являются инерционными звеньями и соответственно равны

Рис. 4.2

Тогда на основании метода суперпозиции установившаяся ошибка САУ

где — ошибка отработки системой задающего воздействия:

а — ошибка, вызванная действием помехи:

В данном случае САУ является статической относительно обоих воздействий, так как .

2. Допустим, что в элемент 2 рассматриваемой системы (рис. 4.2) включено интегрирующее звено, а элемент является инерционным звеном, как и в случае 1. При этом передаточная функция элемента 2

Тогда составляющие ошибки системы (4.9)

Следовательно, САУ является астатической относительно задающего воздействия и статической относительно возмущения

3. Пусть интегрирующее звено включено в элемент передаточная функция его при этом равна

Второе звено является инерционным звеном, а передаточная функция его та же, что и в случае 1.

Рассчитаем составляющие ошибки

Поскольку и система является астатической и относительно воздействия и относительно возмущения

Нужно отметить, что метод коэффициентов ошибок применяется при сравнительно медленно меняющихся воздействиях.

Пример 4.1. Для системы (рис. 4.1) определить значение устано вившейся ошибки системы. Передаточная функция системы в разомкнутом состоянии

где

Выходной сигнал меняется по закону Найдем передаточную функцию замкнутой системы относительно ошибки:

Коэффициенты ошибок так как система астатическая) определяют по (4.7) или разложением в ряд по возрастающим степеням s функции делением числителя на знаменатель:

Коэффициенты вычислять не имеет смысла, так как функция имеет только две производные, не равные нулю.

Определим первую и вторую производные входного воздействия

Тогда

Показатели качества сау

Количественные оценки
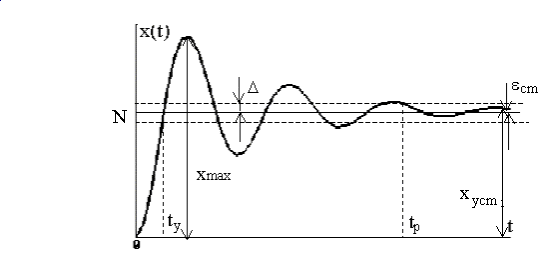
качества, так называемые прямые показатели
качества, определяются по кривой
переходного процесса (рис.16).

Рис.16. Переходная
функция и показатели качества

Используются следующие
прямые показатели качества:

величина
перерегулирования
,

;

характеризует
максимальное отклонение регулируемой
величины от ее установившегося значения,
которое может быть определено в
соответствии с теоремой о конечном
значении оригинала

;

время
переходного процесса или время
регулирования t_p
– наименьшее значение времени, после
которого имеет место неравенство

где

— заданная величина, обычно лежащая в
пределах =0,02÷0,05;

3)
статическая ошибка _с_m–
величина отклонения установившегося
значения регулируемой величины x()
от требуемого значения
N

или
,
гдеE(p)– изображение ошибки;

4)
время регулирования t_р
– промежуток времени, по истечении
которого регулируемая величина первый
раз достигает установившегося значения.

Для определения
качества системы могут использоваться
и другие показатели, соответствующие
решаемой задаче, например, число колебаний
регулируемой величины за время
регулирования, частота и период колебаний
и т.д.

Во всех случаях
необходимо построить переходную функцию.

Коэффициенты ошибок

Точность САУ в
установившемся режиме, при относительно
медленно изменяющихся воздействиях,
может быть оценена с помощью коэффициентов
ошибок. Изображение ошибки определяется
выражением

где
—
передаточная функция по ошибке.

Разложим передаточную
функцию системы по ошибке в степенной
ряд в окрестности точки p=0.
Отметим, что приp0,tи именно
поэтому мы говорим о точности в
установившемся режиме.

Обозначим:
и получим

,
(8)

Учитывая, что оператор
p, умноженный на
изображение самой величины, является
символом дифференцирования, можно для
оригиналов записать

.
(9)

Выражение (9) определяет
зависимость ошибки регулирования от
различных составляющих входного
воздействия, коэффициенты K_iполучили название коэффициентов ошибок:

K₀— коэффициент ошибки по положению;
K₁—
коэффициент ошибки по скорости;
K₂– коэффициент ошибки по ускорению и
т.д.

Из (8) следует, что

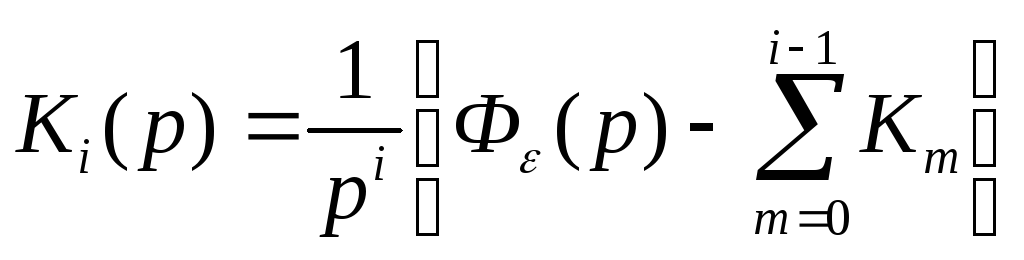
Численные значения
коэффициентов ошибок определяются из
этого выражения при p0.

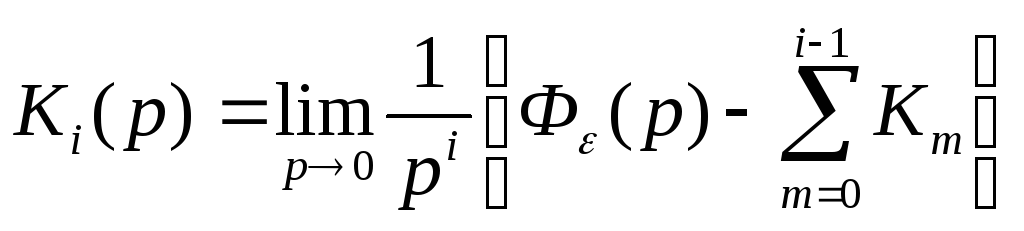
Очевидно, что К₀=Ф_(0).

Входное воздействие
можно представить в виде степенного
ряда

где g₀– постоянная величина, характеризующая
начальное значение, g₁=const – скорость
изменения входного воздействия, g₂=const – ускорение и т.д.

Тогда

Пусть передаточная
функция разомкнутой системы имеет вид

где - порядок астатизма системы. Для
передаточной функции замкнутой системы
по ошибке получим

Изображение ошибки
запишется в виде

Отсюда следует, что
если порядок астатизма больше порядка
старшей производной воздействия, т.е.
>m, то ошибка в
установившемся режиме будет равна нулю.
Если=m, то установившаяся
ошибка будет равна постоянной величине,
называемой статической ошибкой. И если<m, то при tи. В отношении
коэффициентов ошибок последнее выражение
позволяет сделать следующие выводы.

1). Если система
статическая, т.е.=0,
то существуют все составляющие ошибки
и все коэффициенты ошибок не равны нулю,
т.к.К₀ = Ф_(0)
0.

2).Система с астатизмом
1-го порядка, 
=1, не имеет ошибки по положению иК₀=0.

3).Система с астатизмом
2-го порядка, 
=2, не имеет ошибок по положению и по
скорости иК₀ =0,К₁=0.

Этот список можно
продолжить. Таким образом, повышение
порядка астатизма повышает точность
системы в установившемся режиме. Но
повышение порядка астатизма снижает
запасы устойчивости, т.к. введение
интегрирующих звеньев увеличивает
фазовое запаздывание (снижает частоту
). Поэтому на
практике порядок астатизма выше второго
не применяют, а чаще всего ограничиваются
астатизмом первого порядка, используя
для повышения точности другие способы.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Оценка качества регулирования в установившемся режиме (коэффициенты ошибок)

Регулярная оценка качества регулирования (коэффициент ошибок) Рассмотрим показатель качества, который характеризует обязательный компонент системы ошибок ev (/). Постоянная ошибка управления при поступлении сигнала на вход системы (рисунок 4.1) Система ev (f) = xB (t) -g (t), где xv (f) — вынужденная составляющая (4.1) управляющей переменной. Если g (t) дифференцируемо на всем интервале 0 °, Как выразить систему e „(/) как серию 4 (0 = Сов (0 + CtdgU) / дт 4 — Ctd2g (т) fdt2 + ••• + + cmd * g (t) ldtm, (4,8) ми Где коэффициенты C0, Clf C2, … обычно называют коэффициентами ошибки. Уравнение (4.8) получается следующим образом.

Закрытая система передачи функции для ошибок (рисунок 4.1) (S) -1 / | 1 + W (секунды) | = Ea (s) / G (s). (4.9) Из (4.9) вы можете найти уравнение для изображения ошибки Eh (s). Eb (s) = G (s) / | 1+ W (s) |. (4.10) Увеличивая силу s вблизи точки s = 0, передаточная функция неправильно расширяется с помощью номера gt (s). Большое время (t oo), то есть значение ошибки установившегося состояния для данного действия управления. Согласно (4.10), вы можете написать K (s) = [Cv + C, s + i- C2 $ 2 + + •• + ± Cms-] G (s). (4.11) Когда передаточная функция tt + … + vy.15 + vy

Затем вы можете расширить ряд WR (5), разделив числитель на знаменатель и расположив полиномиальные члены в порядке возрастания.

Людмила Фирмаль

Если вы передадите изображение оригиналу в (4.11), вы можете получить выражение (4.8) для ev (/). Коэффициенты ошибок C0, Clt C, … решено! Формула разложения для функции ряда Тейлора IVgt (s) C0 = [WGI (s) Uo, C, — _ rwjjjii Д.С. см = s «o dsm (4.12) с = 0 Если g (t) = 1 (/), все производные dg (t)! Dt-d2g (> t) ‘dt2 = dmg (t)! Dtm = 0 C-W (0) и C __— C dmg (0-0 Кроме того, C0-U ^ Kt (0) — это значение стационарной ошибки замкнутой системы. Если g (t) = ty, dg (t) / dt = l, d2g (t)! Dt2 = •. • = dmg (t) ldtm = 0; -r ^ w = Коэффициент C0 = (0), C, = £ —j- с = 0 = Cmdmg (t) idtm = 0 и т. Д. Коэффициент C называется коэффициентом статической ошибки или ошибки положения. Коэффициент погрешности Ct-Speed; C2 — Коэффициент погрешности от ускорения.

В статических системах коэффициент C0 не равен нулю. С0 = О, С, Ф0 для систем со статистикой первого порядка, С0 = С, = 0, С2 = 0 для систем со статистикой второго порядка. По мере увеличения количества интегрированных ссылок в системе некоторые значения коэффициента ошибок становятся равными нулю, но в то же время обеспечение стабильности системы становится более сложным. Если количество ненулевых производных мастер-действия ограничено, количество членов в ряду (4.8) ограничено. Метод коэффициента ошибок используется для эффектов, которые изменяются относительно медленно. Этот метод был описан выше. Для управляющего воздействия g (t) его также можно применять для оценки точности системы при наличии возмущения / (/).

Например, система 4.1 (рисунок 4.1), определить устойчивое значение системной ошибки. Передаточная функция открытой системы P (s) — * / | s (! -F-s7 ) (1 -f s72) J, Где k = 10 секунд «1. G, = 0,2 секунды, Tg-0,02 секунды. Выходной сигнал изменяется по закону g (l) = • 5 -f 20 / -f 20/2. Найти функцию передачи закрытой системы, связанную с ошибкой w wimgm 1 Ml + srt) (l + s T%) Wgt (s) = E (s) / G (s) = s (I + sr |) (I + sri) + fc & TXT% + s2 (7 4-T2) + s «Она (SJ- EW eT ^ + sP ^ i + r ^ + e + ft

Коэффициенты ошибок Ci и Cg (Co = 0, поскольку система является статической) определяются степенью s функции Wgf (s) (4.12) или расширением n путем деления числителя на знаменатель. (0 = Cxs 4-C + ••• = s / k + s2 (T, + Tg-I / k) / k + Поскольку функция g (t) имеет только две производные, коэффициенты C3, … не имеют смысла. Определите первую и вторую производные входного действия g (t). 2 (0 = 20 4-40 /; £ (0 = 40. затем «в (0 = ev (0 = 2,48 + 4 /.

Смотрите также:

Решение задач по теории автоматического управления

Источник

Оценка качества регулирования в установившемся режиме (коэффициенты ошибок)

Регулярная оценка качества регулирования (коэффициент ошибок) Рассмотрим показатель качества, который характеризует обязательный компонент системы ошибок ev (/). Постоянная ошибка управления при поступлении сигнала на вход системы (рисунок 4.1) Система ev (f) = xB (t) -g (t), где xv (f) — вынужденная составляющая (4.1) управляющей переменной. Если g (t) дифференцируемо на всем интервале 0 °, Как выразить систему e „(/) как серию 4 (0 = Сов (0 + CtdgU) / дт 4 — Ctd2g (т) fdt2 + ••• + + cmd * g (t) ldtm, (4,8) ми Где коэффициенты C0, Clf C2, … обычно называют коэффициентами ошибки. Уравнение (4.8) получается следующим образом.

Затем вы можете расширить ряд WR (5), разделив числитель на знаменатель и расположив полиномиальные члены в порядке возрастания.

Людмила Фирмаль

Например, система 4.1 (рисунок 4.1), определить устойчивое значение системной ошибки. Передаточная функция открытой системы P (s) — * / | s (! -F-s7 ) (1 -f s72) J, Где k = 10 секунд «1. G, = 0,2 секунды, Tg-0,02 секунды. Выходной сигнал изменяется по закону g (l) = • 5 -f 20 / -f 20/2. Найти функцию передачи закрытой системы, связанную с ошибкой w wimgm 1 Ml + srt) (l + s T%) Wgt (s) = E (s) / G (s) = s (I + sr |) (I + sri) + fc & TXT% + s2 (7 4-T2) + s «Она (SJ- EW eT ^ + sP ^ i + r ^ + e + ft

Смотрите также:

Решение задач по теории автоматического управления

Источник

Подборка по базе: Оптимизация бизнес процессов компании путём внедрения CRM.docx, 1 Самостоятельная работа к теме 3.1.2 «Управление качеством Бакл, Ответы НУЦ Качество, ВИК Общий (дополнено).docx, Самостоятельная работа к теме 3.1.2 «Управление качеством образо, Классный час на тему _Воспитанность- необходимое качество личнос, Центральный банк России как органи регулирования банковской сист, Моделирование экономических процессов ,Крылова. Практика. (1).do, Моделирование экономических процессов.Крылова. Практика..docx, Проект. Управление качеством образования.docx, МОДЕЛИРОВАНИЕ СОЦИАЛЬНО-ЭКОНОМИЧЕСКИХ ПРОЦЕССОВ 2.docx

9. Качество процессов регулирования в типовых режимах. Оценка качества регулирования в установившемся режиме

Качество процессов регулирования в типовых режимах Устойчивость является необходимым, но недостаточным условием пригодности САУ для практического использования. Кроме устойчивости САУ должна удовлетворять ряду требований, характеризующих работу системы как в установившемся, так и переходном режимах, т.е. обеспечивать определенное качество регулирования.

Основным показателем, характеризующим качество регулирования в установившемся режиме является точность, которая определяется величиной отклонения регулируемой величины от ее заданного значения после окончания переходного процесса. Рассмотрим показатели, характеризующие качество регулирования в переходном режиме. Эти показатели оцениваются по реакции системы на некоторые тестовые воздействия (единичная ступенчатая, единичная импульсная). Наиболее широко используется ступенчатая функция

В результате на выходе системы получим переходную характеристику, типичный вид которой показан на рисунке . По этому рисунку определим основные прямые оценки качества регулирования системы

Рисунок — Колебательный переходной процесс при единичном ступенчатом воздействии

Основные показатели качества регулирования:

1) Время регулирования – tр. Это длительность переходного процесса от момента приложения к системе воздействия до момента, когда отклонение регулируемой величины h(t) от нового установившегося значения h уст. станет меньше некоторой заданной величины ∆=(1- 5)%

h(t)-h< ∆

2) Перерегулирование σ — максимальное отклонение регулируемой величины h max от нового установившегося значения h уст. в относительных единицах или в %.

σ=(h max – h уст.)/ h уст.*100%, σ=10-30%

3) Частота колебаний

Время достижения первого максимума – t max

5) Время нарастания переходного процесса

Число колебаний – n (за время t p) обычно 1-2, иногда n=0

Кривая переходного процесса может быть получена расчетным путем или экспериментально. В тех случаях, когда это затруднительно, используют косвенные методы оценки качества, а прямые оценки – на заключительном этапе исследования САУ. Косвенные методы оценки качества, не требующие построения графика переходного процесса делятся на три группы: корневые, интегральные и частотные методы. Как было показано выше, вид корней характеристического уравнения определяет характер переходного процесса системы, поэтому можно сформулировать требования, по качеству переходных процессов не рассматривая самих переходных процессов, а накладывая определенные ограничения на корни характеристического уравнения.

АВТОКОЛЕБАНИЯ В НЕЛИНЕЙНЫХ СИСТЕМАХ

Понятие об автоколебаниях Одной из основных особенностей нелинейных систем, как уже отмечалось в разделе 10, является режим автоколебаний. Автоколебания – это устойчивые собственные колебания, возникающие за счет непериодического источника энергии и определяемые свойствами системы.

Этот режим принципиально отличается от колебаний линейной системы на границе устойчивости. В линейной системе при малейшем уменьшении ее параметров колебательный процесс становится либо затухающим, либо расходящимся. Автоколебания же являются устойчивым режимом: малые изменения параметров системы не выводят ее из этого режима.

Амплитуда автоколебаний не зависит от начальных условий и уровня внешних воздействий. Автоколебания в нелинейных системах в общем случае нежелательны, а иногда и недопустимы. Однако, в некоторых нелинейных системах автоколебания являются основным рабочим режимом. Примерами автоколебательных систем являются часы, электрический звонок, всевозможные генераторы; при определенных условиях автоколебания возникают и в химических реакторах.

Для большинства реальных систем определение автоколебаний является сложной проблемой, являясь в то же время одной из задач исследования нелинейных систем. При изучении режима автоколебаний необходимо ответить на вопросы, связанные с условиями их возникновения, числом, параметрами автоколебаний и их устойчивостью. Как известно, на фазовой плоскости автоколебательному режиму соответствует изолированная замкнутая фазовая траектория – предельный цикл.

В связи с этим проследить условия возникновения автоколебаний можно на примере возникновения предельного цикла. Существует два режима возникновения автоколебаний, которые называются режимами мягкого и жесткого возбуждения.

Анализ систем управления. Требования к управлению Что мы хотим от управления? Это зависит, прежде всего, от решаемой задачи. В задаче стабилизации наиболее важны свойства установившегося режима. Для следящих систем в первую очередь нужно обеспечить высокое качество переходных процессов при изменении задающего сигнала (уставки).

В целом можно выделить четыре основных требования:

• точность – в установившемся режиме система должна поддерживать заданное значение выхода системы, причем ошибка (разница между заданным и фактическим значением) не должна превышать допустимую;

• устойчивость – система должна оставаться устойчивой на всех режимах, не должна идти «вразнос» (корабль не должен идти по кругу при смене курса);

• качество переходных процессов – при смене заданного значения система должна переходить в нужное состояние по возможности быстро и плавно;

• робастность – система должна сохранять устойчивость и приемлемое качество даже в том случае, если динамика объекта и свойства внешних возмущений немного отличаются от тех, что использовались при проектировании.

Устойчивость.

Что такое устойчивость? «Бытовое» понятие устойчивости известно нам с детства. Например, табуретка с двумя ножками неустойчива, она упадет при малейшем дуновении ветра, а с тремя – устойчива. Всем знакомый пример неустойчивой системы – близко расположенные микрофон и колонки, которые начинают «свистеть». Неустойчивость может привести к трагическим последствиям. Достаточно вспомнить аварии самолетов, попавших в грозовой фронт или в штопор, взрыв ядерного реактора на Чернобыльской атомной станции в 1986 г.

Термин «устойчивость» используется в численных методах, механике, экономике, социологии, психологии. Во всех этих науках имеют в виду, что устойчивая система возвращается в состояние равновесия, если какая-то сила выведет ее из этого состояния. Шарик на рисунке находится в устойчивом равновесии в положении А – если немного сдвинуть его с места, он скатится обратно в ямку.

Однако мы можем заметить, что если шарик сильно отклонить от равновесия, он может свалиться через горку вбок, то есть устойчивость нарушится. В положениях Б и В шарик также находится в положении равновесия, но оно неустойчиво, так как при малейшем сдвиге в сторону шарик скатывается с вершины. В положениях Г и Д равновесие шарика нейтральное – при небольшом смещении он остается в новом положении. При этом говорят, что система нейтрально устойчива, то есть находится на границе устойчивости.

Можно показать, что система «шарик-горка» – нелинейная. Как мы увидели, для нее

• устойчивость – не свойство системы, а свойство некоторого положения равновесия;

• может быть несколько положений равновесия, из них некоторые – устойчивые, а некоторые – нет;

• положение равновесия может быть устойчиво при малых отклонениях (система устойчива «в малом») и неустойчиво при больших («в большом»).

Устойчивость бывает разная. Известно несколько определений устойчивости, которые отличаются некоторыми деталями. Если рассматривается только выход системы при различных ограниченных входах, говорят об устойчивости «выход-выход».

Кроме того, часто изучают устойчивость автономной системы, на которую не действуют внешние сигналы (все входы нулевые). Предполагается, что систему вывели из положения равновесия (задали ненулевые начальные условия) и «отпустили». Система, которая сама возвращается в исходное положение равновесия, называется устойчивой.

Если при этом рассматривается только выход системы (а не ее внутренние сигналы), говорят о «технической устойчивости» (или устойчивости по выходу). Напротив, внутренняя или математическая устойчивость означает, что не только выход, но и все внутренние переменные (переменные состояния) приближаются к своим значениям в положении равновесия.

В некоторых задачах основной рабочий режим – это периодические колебания, поэтому можно рассматривать устойчивость процессов, а не только положения равновесия. Однако почти все такие системы – нелинейные.

Устойчивость «вход-выход»

Обычно для инженеров практиков в первую очередь важно, чтобы система не «пошла вразнос», то есть, чтобы управляемая величина не росла неограниченно при всех допустимых входных сигналах. Если это так, говорят, что система обладает устойчивостью «вход-выход» (при ограниченном входе выход также ограничен). Заметим, что при этом нас не интересует, как меняются внутренние переменные объекта, важен только вход и выход.

Рассмотрим ванну, которая наполняется водой из крана. Модель этой системы – интегрирующее звено. При постоянном (ограниченном по величине!) входном потоке уровень воды в ванне будет неограниченно увеличиваться (пока вода не польется через край), поэтому такая система не обладает устойчивостью «вход-выход».

Техническая» устойчивость

В отличие от устойчивости «вход-выход», понятие «техническая устойчивость» относится к автономной системе, у которой все входные сигналы равны нулю. Положением равновесия называют состояние системы, которая находится в покое, то есть, сигнал выхода y(t) – постоянная величина, и все его производные равны нулю. Систему выводят из положения равновесия и убирают все возмущения. Если при этом с течением времени (при t → ∞ ) система возвращается в положение равновесия, она называется устойчивой. Если выходная координата остается ограниченной (не уходит в бесконечность), система называется нейтрально устойчивой, а если выход становится бесконечным – неустойчивой.

Если вернуться к примеру с ванной, становится понятно, что эта система – нейтрально устойчива, потому что уровень воды остается постоянным, когда мы перекроем кран. С одной стороны, уровень воды не возвращается к предыдущему значению, а с другой – не растет бесконечно (система не является неустойчивой).

Критерии устойчивости

Для исследования устойчивости линейной системы достаточно найти корни ее характеристического полинома. Если все корни имеют отрицательные вещественные части (находятся в левой полуплоскости, слева от мнимой оси), такой полином называется устойчивым, потому что соответствующая линейная система устойчива. Полиномы, имеющие хотя бы один корень с положительной вещественной частью (в правой полуплоскости) называются неустойчивыми. На ранней стадии развития теории управления актуальной была задача определения устойчивости полинома без вычисления его корней.

Конечно, сейчас легко найти корни характеристического полинома с помощью компьютерных программ, однако такой подход дает нам только количественные (а не качественные) результаты и не позволяет исследовать устойчивость теоретически, например, определять границы областей устойчивости.

Робастность.

Что такое робастность? Обычно регулятор строится на основе некоторых приближенных (номинальных) моделей объекта управления (а также приводов и датчиков) и внешних возмущений. При этом поведение реального объекта и характеристики возмущений могут быть несколько иными.

Поэтому требуется, чтобы разработанный регулятор обеспечивал устойчивость и приемлемое качество системы при малых отклонениях свойств объекта и внешних возмущений от номинальных моделей. В современной теории управления это свойство называют робастностью (грубостью). Иначе его можно назвать нечувствительностью к малым ошибкам моделирования объекта и возмущений.

Различают несколько задач, связанных с робастностью:

робастная устойчивость – обеспечить устойчивость системы при всех допустимых отклонениях модели объекта от номинальной;
робастное качество – обеспечить устойчивость и заданные показатели качества системы при всех допустимых отклонениях модели объекта от номинальной;
гарантирующее управление – обеспечить заданные показатели качества системы при всех допустимых отклонениях модели возмущения от номинальной (считая, что модель объекта известна точно). Для того, чтобы исследовать робастность системы, нужно как-то определить возможную ошибку моделирования (неопределенность). Ее можно задать различными способами

Понятие о дискретных системах автоматического управления и их классификация по виду дискретизации (квантования) сигнала

В рассмотренных ранее непрерывных системах сигналы, несущие информацию о состоянии переменных системы, представляют собой непрерывные функции времени. Помимо непрерывных способов передачи и преобразования сигналов широко применяются дискретные способы, в которых используется в том или ином виде дискретизация сигнала. Дискретизация сигнала состоит в замене непрерывного сигнала теми или иными дискретными значениями и может быть осуществлена по уровню, по времени либо по времени и по уровню.

Дискретизация, или квантование сигнала по уровню соответствует выделению значений сигнала при достижении им заранее фиксированных уровней. Дискретизация, или квантование сигнала по времени соответствует выделению значений сигнала в заранее фиксированные моменты времени. Дискретизация сигнала по времени и по уровню соответствует выделению в заранее фиксированные моменты времени значений сигнала, ближайших к заранее фиксированным уровням.

В зависимости от типа квантования, которое используется в автоматических системах, они подразделяются на 3 вида.

Релейные системы ⎯ если хотя бы одна из величин, характеризующих состояние системы, квантуется по уровню.

Импульсные системы ⎯ если хотя бы одна из величин, характеризующих состояние системы, квантуется по времени.

Цифровые системы ⎯ если хотя бы одна из величин, характеризующих состояние системы, квантуется и по времени, и по уровню.

Существуют системы, в которых используется два и все три вида дискретизации сигналов.

Позиционные системы автоматического регулирования

Позиционной называют систему, в которой управляющее воздействие на объект ступенчато изменяется в зависимости от уровня ошибки. Соответственно, позиционным называют закон регулирования, когда управляющее воздействие на объект принимает ряд постоянных дискретных значений (изменяется ступенчато) в зависимости от ошибки системы.

Позиционные системы относятся к наиболее простым и распространенным релейным системам.

Двухпозиционной САР называется система, в которой управляющее воздействие на объект приобретает два значения.

Трёхпозиционной САР называется система, в которой управляющее воздействие на объект приобретает три значения.

Существуют также четырехпозиционные системы и т.д.

Примерами позиционных систем являются системы регулирования температуры в холодильнике, температуры подошвы утюга. Эти системы являются двухпозиционными, поскольку управляющее воздействие на объект принимает два значения. Например, при пониженной температуре подошвы утюга питание нагревательного элемента включается, при повышенной температуре ⎯ выключается.

В сельском хозяйстве позиционное регулирование применяется в системах регулирования микроклимата животноводческих помещений, регулирования температуры инкубаторов, температуры теплоносителя зерновых сушилок и т.д.

Пример. Процесс нагрева и охлаждения воздуха в сушильной камере повторяется. В сушильной камере устанавливается режим периодического нагрева и охлаждения. Такие установившиеся режимы работы называют автоколебательными.

Автоколебательные режимы часто возникают в нелинейных системах. В частности они характерны для позиционных систем. На рис. изображен процесс регулирования температуры в сушильной камере после включения системы.

Процесс регулирования температуры в сушильной камере, обеспечиваемый двухпозиционной системой

Понятие об анализе и синтезе САУ

Целью рассмотрения системы автоматического управления может быть решение одной из двух задач ⎯ задачи анализа системы или задачи ее синтеза. В первом случае дается система, включая значения параметров, и требуется оценить ее свойства, т.е. качество управления, обеспечиваемое системой.

Во втором случае, наоборот, задаются свойства, которыми должна обладать система, т.е. требования к ней, и необходимо создать систему, удовлетворяющую этим требованиям. Задача синтеза имеет неоднозначное решение и много сложнее задачи анализа. В самом общем виде порядок исследования САР в обоих случаях включает математическое описание системы, исследование ее установившихся и переходных режимов.

Общие принципы математического описания систем автоматического управления

Математическое описание (математические модели) систем составляют на основании законов той области знаний, к которой относится объект управления и технические средства автоматики, образующие управляющее устройство. Если теоретическим путем математическое описание какого-либо объекта получить затруднительно или невозможно, то прибегают к идентификации этого объекта

По математическому описанию системы классифицируются на линейные и нелинейные. Линейные системы ⎯ это системы, описанные только линейными уравнениями. Нелинейные системы ⎯ это системы, математическое описание которых содержит хотя бы одно нелинейное звено.

Линейное математическое описание почти всегда является приближенным. Такое приближенное математическое описание, если это допустимо, делают для облегчения исследования систем.

Математическое описание систем разбивают на отдельные звенья, передающие сигнал только в одном направлении ⎯ со входа на выход. Такие звенья называют звеньями направленного действия. Из звеньев составляют структурные схемы.

Структурной схемой называется наглядное графическое изображение математической модели (математического описания) системы. На структурной схеме каждое звено изображается прямоугольником, внутри которого записывается математическое описание звена. Связи между звеньями структурной схемы изображаются линиями со стрелками, соответствующими направлению прохождения сигналов. Над линиями ставятся обозначения сигналов.

Для синтеза и анализа САУ необходимо иметь математические модели объекта управления и средств, входящих в систему (далее просто объектов). Теоретически их можно получить путем составления дифференциальных уравнений. Однако в большинстве случаев точное математическое описание объектов получить весьма затруднительно из-за сложности протекающих в них процессов и недостатка исходной информации. Поэтому на практике часто математические модели получают путем идентификации

Идентификацией называют получение математической модели объекта на основании совместного анализа входных воздействий на объект и реакции объекта на эти воздействия. При идентификации объект рассматривается как черный ящик, математическую модель которого необходимо найти.

Общий порядок идентификации следующий.

На объект подаются тестирующие воздействия. Если объект идентифицируется в условиях эксплуатации, то записываются воздействия в этих условиях. Записывается реакция объекта на эти воздействия.
На основании совместного анализа воздействия на объект и реакции объекта и с привлечением всех априорных сведений о структуре объекта формируется гипотеза о структуре математического описания (модели) объекта. Оцениваются параметры модели.

3. Путем сравнения экспериментально полученной реакции и расчетной по модели уточняются параметры математической модели. Если расчетная реакция достаточно точно аппроксимирует экспериментальную реакцию, то гипотеза принимается. В противном случае необходимо выдвигать новую гипотезу о структуре объекта и повторять ее проверку.

Идентификация сложных, особенно нелинейных, объектов часто оказывается трудоемкой и нетривиальной задачей. Конкретные методы ее решения определяются предполагаемой структурой объекта и формой воздействий. Наиболее просто решается вопрос идентификации линейных объектов при типовых воздействиях, поскольку в этом случае зависимость реакции объекта от вида передаточной функции (дифференциального уравнения) объекта достаточно известна. Наиболее распространенной является идентификация линейных объектов по переходной функции ⎯ реакции объекта на ступенчатое воздействие.

Источник

Показатели качества сау

Коэффициенты ошибок

Оценка качества регулирования в установившемся режиме (коэффициенты ошибок)

Оценка качества регулирования в установившемся режиме (коэффициенты ошибок)

9. Качество процессов регулирования в типовых режимах. Оценка качества регулирования в установившемся режиме

Возможно, вам также будет интересно: