Классификация методов контроля достоверности по степени выявления и коррекции ошибок
По степени выявления и коррекции ошибок
контроль делится на:
-
обнаруживающий,
фиксирующий только сам факт наличия
или отсутствия ошибки; -
локализующий,
позволяющий определить как факт наличия,
так и место ошибки (например символ,
реквизит и т. д.); -
исправляющий,
выполняющий функции и обнаружения, и
локализации, и исправления ошибки.
В работах [6, 8] приведен обширный список
методов контроля достоверности информации
(более 100 методов), в том числе методы,
использующие контрольные суммы и
контрольные байты, коды с обнаружением
и автоматическим исправлением ошибок
(корректирующие коды); методы семантического
и балансового контроля, методы
алгоритмического и эвристического
контроля, методы верификации, прямого
и обратного преобразования (передачи)
информации и т. д.
Основные показатели качества контроля достоверности
Функциональные показатели
качества контроля (показатели
его эффективности) должны количественно
определять степень приспособленности
и выполнения контролем поставленных
перед ним задач. В общем случае контроля
такими показателями могут служить
коэффициенты, численно равные условным
вероятностям соответствующих событий
при условии наличия ошибки.
Для обнаруживающего и локализующего
контроля такими коэффициентами являются:
-
коэффициент обнаружения ошибок —
Kобн = Nобн / Nош = Pобн / Pош; -
коэффициент необнаружения ошибок —
Kно = Nно / Nош = Pно / Pош; -
коэффициент локализации ошибок Клок
для большинства методов локализующего
контроля равен коэффициенту обнаружения,
то есть Клок = Кобн.
Методы контроля, исправляющие ошибки,
характеризуются следующими коэффициентами:
-
исправления ошибок
Kиспр = Nиспр / Nош = Pиспр / Pош; -
искажения ошибок Kиск = Nиск / Nош = Pиск / Pош;
-
обнаружения ошибок Kобн = Nобн / Nош = Pобн / Pош;
-
не-обнаружения ошибок
Kно = Nно / Nош = Pно / Pош.
В этих соотношениях:
-
N — число структурных
элементов (символов, реквизитов,
показателей и т. д.) в информационной
совокупности; -
Nно, Nиспр,
Nиск, Nобн —
число ошибок, которые в процессе
контроля, соответственно, не обнаруживаются,
правильно исправляются, неверно
исправляются (искажаются), только
обнаруживаются (факт наличия которых
просто устанавливается, а сами они не
исправляются); -
Рош, Робн,
Рно, Риспр,
Риск —
вероятности наличия ошибки, обнаружения,
не-обнаружения, исправления и искажения
ошибки, соответственно.
Важными показателями качества контроля
являются также:
-
коэффициент выявления ошибок
Kвыявл = Nвыявл / Nош,
характеризующий суммарное относительное
число выявляемых (Nвыявл)
ошибок в контролируемой информационной
совокупности; -
коэффициент трансформации ошибок
Kтр = Nош.вых / Nош,
характеризующий суммарное относительное
число необнаруженных и вновь внесенных
при контроле (Nош.вых)
ошибок.
Для контроля с
исправлением ошибок:
Квыявл
= Киспр + Киск
+ Кобн;
Ктр
= Кно + Киск.
Для контроля с обнаружением ошибок:
Киспр
= Киск = 0
Квыявл
= Кобн,
Ктр
= Кно
В качестве дополнительных функциональных
показателей могут быть использованы
значения вероятности правильного
необнаружения ошибки и ложного обнаружения
ошибки, учитывающие надежность работы
системы контроля:
-
Рпр —
вероятность правильного необнаружения
ошибки, то есть такого события, когда
не вырабатывается информация о наличии
ошибки при условии действительного ее
отсутствия; -
Рлт —
вероятность ложного обнаружения ошибки
(ложной тревоги), то есть такого события,
когда вырабатывается информация о
наличии ошибки при реальном ее отсутствии.
Технико-эксплуатационные показатели
контроля:
-
алгоритмическая сложность контроля;
-
вид и величина используемой избыточности;
-
надежность контроля;
-
универсальность (возможность использования
на различных фазах технологического
процесса, при решении различных задач
и для различных групп и типов информационных
ошибок) и др.
Соответствующие коэффициенты
Kпр = Pпр / Pош,
Kиг = Pиг / Pош
могут быть существенно больше 1,
поскольку Kпр + Kлт = (1 – Pош)/Pош.
Экономические показатели эффективности
контроля — это затраты на контроль:
-
единовременные;
-
текущие;
-
материальные;
-
трудовые;
-
временные.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Аннотация: Контроль по четности, CRC, алгоритм Хэмминга. Введение в коды Рида-Соломона: принципы, архитектура и реализация. Метод коррекции ошибок FEC (Forward Error Correction).
Каналы передачи данных ненадежны (шумы, наводки и т.д.), да и само оборудование обработки информации работает со сбоями. По этой причине важную роль приобретают механизмы детектирования ошибок. Ведь если ошибка обнаружена, можно осуществить повторную передачу данных и решить проблему. Если исходный код по своей длине равен полученному коду, обнаружить ошибку передачи не предоставляется возможным. Можно, конечно, передать код дважды и сравнить, но это уже двойная избыточность.
Простейшим способом обнаружения ошибок является контроль по четности. Обычно контролируется передача блока данных ( М бит). Этому блоку ставится в соответствие кодовое слово длиной N бит, причем N>M. Избыточность кода характеризуется величиной 1-M/N. Вероятность обнаружения ошибки определяется отношением M/N (чем меньше это отношение, тем выше вероятность обнаружения ошибки, но и выше избыточность).
При передаче информации она кодируется таким образом, чтобы с одной стороны характеризовать ее минимальным числом символов, а с другой – минимизировать вероятность ошибки при декодировании получателем. Для выбора типа кодирования важную роль играет так называемое расстояние Хэмминга.
Пусть А и Б — две двоичные кодовые последовательности равной длины. Расстояние Хэмминга между двумя этими кодовыми последовательностями равно числу символов, которыми они отличаются. Например, расстояние Хэмминга между кодами 00111 и 10101 равно 2.
Можно показать, что для детектирования ошибок в n битах схема кодирования требует применения кодовых слов с расстоянием Хэмминга не менее N + 1. Можно также показать, что для исправления ошибок в N битах необходима схема кодирования с расстоянием Хэмминга между кодами не менее 2N + 1. Таким образом, конструируя код, мы пытаемся обеспечить расстояние Хэмминга между возможными кодовыми последовательностями большее, чем оно может возникнуть из-за ошибок.
Широко распространены коды с одиночным битом четности. В этих кодах к каждым М бит добавляется 1 бит, значение которого определяется четностью (или нечетностью) суммы этих М бит. Так, например, для двухбитовых кодов 00, 01, 10, 11 кодами с контролем четности будут 000, 011, 101 и 110. Если в процессе передачи один бит будет передан неверно, четность кода из М+1 бита изменится.
Предположим, что частота ошибок ( BER – Bit Error Rate) равна р = 10-4. В этом случае вероятность передачи 8 бит с ошибкой составит 1 – (1 – p)8 = 7,9 х 10-4. Добавление бита четности позволяет детектировать любую ошибку в одном из переданных битах. Здесь вероятность ошибки в одном из 9 битов равна 9p(1 – p)8. Вероятность же реализации необнаруженной ошибки составит 1 – (1 – p)9 – 9p(1 – p)8 = 3,6 x 10-7. Таким образом, добавление бита четности уменьшает вероятность необнаруженной ошибки почти в 1000 раз. Использование одного бита четности типично для асинхронного метода передачи. В синхронных каналах чаще используется вычисление и передача битов четности как
для строк, так и для столбцов передаваемого массива данных. Такая схема позволяет не только регистрировать, но и исправлять ошибки в одном из битов переданного блока.
Контроль по четности достаточно эффективен для выявления одиночных и множественных ошибок в условиях, когда они являются независимыми. При возникновении ошибок в кластерах бит метод контроля четности неэффективен, и тогда предпочтительнее метод вычисления циклических сумм ( CRC — Cyclic Redundancy Check). В этом методе передаваемый кадр делится на специально подобранный образующий полином. Дополнение остатка от деления и является контрольной суммой.
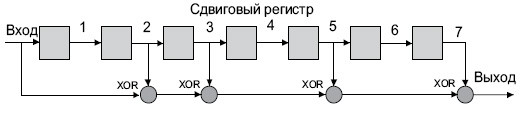
В Ethernet вычисление CRC производится аппаратно. На
рис.
4.1 показан пример реализации аппаратного расчета CRC для образующего полинома R(x) = 1 + x2 + x3 + x5 + x7. В этой схеме входной код приходит слева.
Рис.
4.1.
Схема реализации расчета CRC
Эффективность CRC для обнаружения ошибок на многие порядки выше простого контроля четности. В настоящее время стандартизовано несколько типов образующих полиномов. Для оценочных целей можно считать, что вероятность невыявления ошибки в случае использования CRC, если ошибка на самом деле имеет место, равна (1/2)r, где r — степень образующего полинома.
| CRC -12 | x12 + x11 + x3 + x2 + x1 + 1 |
| CRC -16 | x16 + x15 + x2 + 1 |
| CRC -CCITT | x16 + x12 + x5 + 1 |
4.1. Алгоритмы коррекции ошибок
Исправлять ошибки труднее, чем их детектировать или предотвращать. Процедура коррекции ошибок предполагает два совмещеных процесса: обнаружение ошибки и определение места (идентификации сообщения и позиции в сообщении). После решения этих двух задач исправление тривиально — надо инвертировать значение ошибочного бита. В наземных каналах связи, где вероятность ошибки невелика, обычно используется метод детектирования ошибок и повторной пересылки фрагмента, содержащего дефект. Для спутниковых каналов с типичными для них большими задержками системы коррекции ошибок становятся привлекательными. Здесь используют коды Хэмминга или коды свертки.
Код Хэмминга представляет собой блочный код, который позволяет выявить и исправить ошибочно переданный бит в пределах переданного блока. Обычно код Хэмминга характеризуется двумя целыми числами, например, (11,7), используемыми при передаче 7-битных ASCII-кодов. Такая запись говорит, что при передаче 7-битного кода используется 4 контрольных бита (7 + 4 = 11). При этом предполагается, что имела место ошибка в одном бите и что ошибка в двух или более битах существенно менее вероятна. С учетом этого исправление ошибки осуществляется с определенной вероятностью. Например, пусть возможны следующие правильные коды (все они, кроме первого и последнего, отстоят друг от друга на расстояние Хэмминга 4):
00000000
11110000
00001111
11111111
При получении кода 00000111 нетрудно предположить, что правильное значение полученного кода равно 00001111. Другие коды отстоят от полученного на большее расстояние Хэмминга.
Рассмотрим пример передачи кода буквы s = 0x073 = 1110011 с использованием кода Хэмминга (11,7). Таблица 4.2.
| Позиция бита | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Значение бита | 1 | 1 | 1 | * | 0 | 0 | 1 | * | 1 | * | * |
Символами * помечены четыре позиции, где должны размещаться контрольные биты. Эти позиции определяются целой степенью 2 (1, 2, 4, 8 и т.д.). Контрольная сумма формируется путем выполнения операции XoR (исключающее ИЛИ) над кодами позиций ненулевых битов. В данном случае это 11, 10, 9, 5 и 3. Вычислим контрольную сумму:
| 11= | 1011 |
| 10= | 1010 |
| 09= | 1001 |
| 05= | 0101 |
| 03= | 0011 |
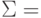 |
1110 |
Таким образом, приемник получит код
| Позиция бита | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Значение бита | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 |
Просуммируем снова коды позиций ненулевых битов и получим нуль;
| 11= | 1011 |
| 10= | 1010 |
| 09= | 1001 |
| 08= | 1000 |
| 05= | 0101 |
| 04= | 0100 |
| 03= | 0011 |
| 02= | 0010 |
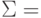 |
0000 |
Ну а теперь рассмотрим два случая ошибок в одном из битов посылки, например в бите 7 (1 вместо 0) и в бите 5 (0 вместо 1). Просуммируем коды позиций ненулевых битов еще раз:
|
|
В обоих случаях контрольная сумма равна позиции бита, переданного с ошибкой. Теперь для исправления ошибки достаточно инвертировать бит, номер которого указан в контрольной сумме. Понятно, что если ошибка произойдет при передаче более чем одного бита, код Хэмминга при данной избыточности окажется бесполезен.
В общем случае код имеет N = M + C бит и предполагается, что не более чем один бит в коде может иметь ошибку. Тогда возможно N+1 состояние кода (правильное состояние и n ошибочных). Пусть М = 4, а N = 7, тогда слово-сообщение будет иметь вид: M4, M3, M2, C3, M1, C2, C1. Теперь попытаемся вычислить значения С1, С2, С3. Для этого используются уравнения, где все операции представляют собой сложение по модулю 2:
С1 = М1 + М2 + М4 С2 = М1 + М3 + М4 С3 = М2 + М3 + М4
Для определения того, доставлено ли сообщение без ошибок, вычисляем следующие выражения (сложение по модулю 2):
С11 = С1 + М4 + М2 + М1 С12 = С2 + М4 + М3 + М1 С13 = С3 + М4 + М3 + М2
Результат вычисления интерпретируется следующим образом:
| C11 | C12 | C13 | Значение |
|---|---|---|---|
| 1 | 2 | 4 | Позиция бит |
| 0 | 0 | 0 | Ошибок нет |
| 0 | 0 | 1 | Бит С3 неверен |
| 0 | 1 | 0 | Бит С2 неверен |
| 0 | 1 | 1 | Бит M3 неверен |
| 1 | 0 | 0 | Бит С1 неверен |
| 1 | 0 | 1 | Бит M2 неверен |
| 1 | 1 | 0 | Бит M1 неверен |
| 1 | 1 | 1 | Бит M4 неверен |
Описанная схема легко переносится на любое число n и М.
Число возможных кодовых комбинаций М помехоустойчивого кода делится на n классов, где N — число разрешенных кодов. Разделение на классы осуществляется так, чтобы в каждый класс вошел один разрешенный код и ближайшие к нему (по расстоянию Хэмминга ) запрещенные коды. В процессе приема данных определяется, к какому классу принадлежит пришедший код. Если код принят с ошибкой, он заменяется ближайшим разрешенным кодом. При этом предполагается, что кратность ошибки не более qm.
В теории кодирования существуют следующие оценки максимального числа N n -разрядных кодов с расстоянием D.
| d=1 | n=2n |
| d=2 | n=2n-1 |
| d=3 | N 2n/(1 + n) |
| d = 2q + 1 | (для кода Хэмминга это неравенство превращается в равенство) |
В случае кода Хэмминга первые k разрядов используются в качестве информационных, причем
K = n – log(n + 1), откуда следует (логарифм по основанию 2), что k может принимать значения 0, 1, 4, 11, 26, 57 и т.д., это и определяет соответствующие коды Хэмминга (3,1); (7,4); (15,11); (31,26); (63,57) и т.д.
Обобщением кодов Хэмминга являются циклические коды BCH (Bose-Chadhuri-hocquenghem). Эти коды имеют широкий выбор длин и возможностей исправления ошибок.
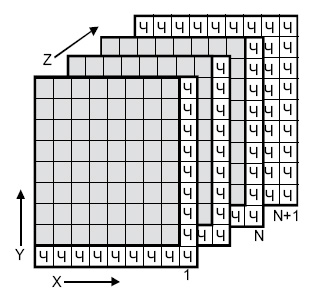
Одной из старейших схем коррекции ошибок является двух-и трехмерная позиционная схема (
рис.
4.2). Для каждого байта вычисляется бит четности (бит <Ч>, направление Х). Для каждого столбца также вычисляется бит четности (направление Y. Производится вычисление битов четности для комбинаций битов с координатами (X,Y) (направление Z, слои с 1 до N ). Если при транспортировке будет искажен один бит, он может быть найден и исправлен по неверным битам четности X и Y. Если же произошло две ошибки в одной из плоскостей, битов четности данной плоскости недостаточно. Здесь поможет плоскость битов четности N+1.
Таким образом, на 512 передаваемых байтов данных пересылается около 200 бит четности.
Рис.
4.2.
Позиционная схема коррекции ошибок
Дисциплина: ТЕХНОЛОГИИ ФИЗИЧЕСКОГО УРОВНЯ
ПЕРЕДАЧИ ДАННЫХ
Занятие №10
Методы обнаружения и коррекции ошибок
при передаче информации в компьютерных сетях.
ПЛАН ЗАНЯТИЯ:
1. Обнаружение и коррекция ошибок
2. Методы обнаружения ошибок
3. Методы коррекции ошибок
4. Вопросы
Обнаружение и коррекция ошибок
Надежную передачу
информации обеспечивают различные методы. Основной
принцип работы протоколов, которые
обеспечивают надежность передачи информации —
повторная передача искаженных или потерянных
пакетов.
Такие протоколы
основаны на том, что приемник в состоянии распознать факт искажения информации
в принятом кадре информации.
Еще одним, более
эффективным подходом, чем повторная передача пакетов,
является использование самокорректирующихся
кодов, которые позволяют не только
обнаруживать, но и исправлять ошибки в
принятом кадре.
Методы обнаружения ошибок
Методы
обнаружения ошибок основаны на передаче в составе блока данных
избыточной служебной информации, по которой можно судить с некоторой степенью
вероятности о достоверности принятых данных. В
сетях с коммутацией пакетов такой
единицей информации может быть PDU
любого уровня, для определенности будем
считать, что мы контролируем кадры.
Избыточную
служебную информацию принято называть контрольной суммой,
или контрольной последовательностью
кадра (Frame Check Sequence, FCS).
Контрольная сумма
вычисляется как функция от основной информации, причем не
обязательно путем суммирования.
Принимающая
сторона повторно вычисляет контрольную сумму кадра по
известному алгоритму и в случае ее совпадения
с контрольной суммой, вычисленной
передающей стороной, делает вывод о том,
что данные были переданы через сеть
корректно.
Рассмотрим
несколько распространенных алгоритмов вычисления контрольной
суммы, отличающихся вычислительной
сложностью и способностью обнаруживать
ошибки в данных.
Контроль по
паритету.
Контроль по
паритету представляет собой наиболее простой метод контроля
данных. В то же время это наименее мощный
алгоритм контроля, так как с его помощью
можно обнаруживать только одиночные
ошибки в проверяемых данных.
Метод заключается в
суммировании по модулю 2 всех битов контролируемой информации.
Нетрудно заметить, что для информации,
состоящей из нечетного числа единиц,
контрольная сумма всегда равна 1, а при четном
числе единиц — 0.
Например, для данных 100101011 результатом контрольного суммирования будет
значение 1. Результат суммирования также
представляет собой один дополнительный бит
данных, который пересылается вместе с
контролируемой информацией. При искажении в
процессе пересылки любого одного бита исходных
данных (или контрольного разряда)
результат суммирования будет отличаться
от принятого контрольного разряда, что
говорит об ошибке.
Однако двойная
ошибка, например 110101010, будет неверно принята за
корректные данные.
Поэтому контроль по паритету применяется к небольшим порциям
данных, как правило, к каждому байту, что дает
коэффициент избыточности для этого
метода 1/8.
Метод редко
используется в компьютерных сетях из-за значительной
избыточности и невысоких диагностических
возможностей.
Вертикальный и
горизонтальный контроль по паритету
Вертикальный и
горизонтальный контроль по паритету представляет собой
модификацию описанного метода. Его отличие
состоит в том, что исходные данные
рассматриваются в виде матрицы, строки
которой составляют байты данных.
Контрольный разряд
подсчитывается отдельно для каждой строки и для каждого столбца
матрицы. Этот метод позволяет обнаруживать
большую часть двойных ошибок, однако он
обладает еще большей избыточностью. На
практике этот метод сейчас также почти не
применяется при передаче информации по сети.
Циклический избыточный контроль
Циклический
избыточный контроль (Cyclic Redundancy Check, CRC) является в
настоящее время наиболее популярным методом
контроля в вычислительных сетях (и не
только в сетях, например, этот метод широко
применяется при записи данных на гибкие и
жесткие диски).
Метод основан на
представлении исходных данных в виде одного многоразрядного
двоичного числа.
Например, кадр стандарта Ethernet, состоящий из 1024 байт, рассматривается как
одно число, состоящее из 8192 бит. Контрольной
информацией считается остаток от
деления этого числа на известный делитель R.
Обычно в качестве делителя выбирается
семнадцати- или тридцатитрехразрядное число,
чтобы остаток от деления имел длину 16
разрядов (2 байт) или 32 разряда (4 байт).
При получении кадра
данных снова вычисляется остаток от деления на тот же делитель R, но при этом к
данным кадра добавляется и содержащаяся в нем контрольная сумма.
Если остаток от
деления на R равен нулю, то делается вывод об отсутствии ошибок в полученном
кадре, в противном случае кадр считается искаженным.
Этот метод
обладает более высокой вычислительной сложностью, но его
диагностические возможности гораздо выше, чем
у методов контроля по паритету.
Этот метод
позволяет обнаруживать все одиночные ошибки, двойные ошибки и
ошибки в нечетном числе битов.
Метод обладает
также невысокой степенью избыточности. Например, для кадра
Ethernet размером 1024 байт контрольная
информация длиной 4 байт составляет только
0,4 %.
Методы коррекции ошибок
Техника
кодирования, которая позволяет приемнику не только понять, что
присланные данные содержат ошибки, но и
исправить их, называется прямой
коррекцией ошибок — (Forward Error Correction, FEC).
Коды, которые
обеспечивают прямую коррекцию ошибок, требуют введения большей избыточности в
передаваемые данные, чем коды, только обнаруживающие ошибки.
При применении
любого избыточного кода не все комбинации кодов являются
разрешенными. Например, контроль по паритету
делает разрешенными только половину
кодов.
Если мы
контролируем три информационных бита, то разрешенными 4-битными
кодами с дополнением до нечетного количества
единиц будут:
000 1, 001 0, 010 0, 011 1, 100
0, 101 1, 110 1, 111 0
То есть всего 8 кодов из 16 возможных.
Для того чтобы
оценить количество дополнительных битов, требуемых для
исправления ошибок, нужно знать так
называемое расстояние Хемминга между
разрешенными комбинациями кода.
Расстоянием
Хемминга называется минимальное число битовых разрядов, в
которых отличается любая пара разрешенных
кодов.
Для схем контроля
по паритету расстояние Хемминга равно 2.
Можно доказать, что если мы сконструировали
избыточный код с расстоянием
Хемминга, равным N, то
такой код будет в состоянии распознавать (N-1)-кратные
ошибки
и исправлять (N-1)/2-кратные
ошибки.
Так как коды с
контролем по паритету имеют расстояние Хемминга, равное 2, то
они могут только обнаруживать однократные
ошибки и не могут исправлять ошибки.
Коды Хемминга
эффективно обнаруживают и исправляют изолированные ошибки,
то есть отдельные искаженные биты,
которые разделены большим количеством
корректных битов.
Однако при
появлении длинной последовательности искаженных битов (пульсации
ошибок) коды Хемминга не работают.
Пульсации ошибок
характерны для беспроводных каналов, в которых применяют
сверточные коды.
Поскольку для распознавания наиболее вероятного корректного кода в
этом методе задействуется решетчатая
диаграмма, то такие коды еще называют
решетчатыми.
Эти коды
используются не только в беспроводных каналах, но и в модемах.
Методы прямой коррекции ошибок особенно
эффективны для технологий
физического уровня, которые не поддерживают
сложные процедуры повторной передачи
данных в случае их искажения.
Вопросы
:
1. Что называется контрольной
последовательностью кадра?
2. Что представляет собой контроль по
паритету?
3. Что представляет собой вертикальный и
горизонтальный контроль по паритету?
4. Что представляет собой циклический избыточный
контроль?
5. Что называется прямой коррекцией ошибок?
6. Что называется расстоянием Хемминга?
7. Какие коды называются решетчатыми?
8. Где используются решетчатые коды?