Методы и приборы для измерения ошибок

Содержание:

Введение

В наиболее широком смысле к «измерениям» относят обнаружение наличия или отсутствия каких-либо свойств, качественную оценку любого свойства, сопоставление величин с нормами, оценку свойства по косвенным показателям и ряд других действий. В отличие от геометрии, социометрии, антропометрии, и квалиметрии, имеющей наиболее широкий набор объектов оценки, метрология занимается измерениями физических величин. Потому мы не будем рассматривать получение экспертных оценок, а сосредоточимся только на измерениях тех параметров, которые подлежат объективной оценке с использованием средств измерений. Такие параметры в большинстве представляют собой физические величины, а их экспериментальные оценки называют аппаратурными или инструментальными в отличие от экспертных (органолептических) оценок, при получении которых инструментарием являются чувства человека.

Виды, методы и классы измерений

Измерение — процесс, заключающийся в сравнении путем физического эксперимента данной ФВ с известной ФВ, принятой за единицу измерения.

Результатом процесса является значение физической величины Q = q[Q] , где q — числовое значение физической величины в принятых единицах; [Q] — единица физической величины. Значение физической величины Q, найденное при измерении, называют действительным.

Принцип измерений — физическое явление или совокупность физических явлений, положенных в основу измерений. Например, измерение массы тела при помощи взвешивания с использованием силы тяжести, пропорциональной массе, измерение температуры с использованием термоэлектрического эффекта.

Метод измерений — совокупность приемов использования принципов и средств измерений.

Средствами измерений (СИ) являются используемые технические средства, имеющие нормированные метрологические свойства.

По характеру зависимости измеряемой величины от времени измерения выделяют статические и динамические измерения.

Статические — это измерения, при которых измеряемая величина остается постоянной во времени. Такими измерениями являются, например, измерения размеров изделия, величины постоянного давления, температуры и др.

Динамические — это измерения, в процессе которых измеряемая величина изменяется во времени, например, измерение давления и температуры при сжатии газа в цилиндре двигателя.

По способу получения результатов, определяемому видом уравнения измерений, выделяют прямые, косвенные, совокупные и совместные измерения.

Прямые — это измерения, при которых искомое значение физической величины находят непосредственно из опытных данных.

Примерами таких измерений являются: измерение длины линейкой или рулеткой, измерение диаметра штангенциркулем или микрометром, измерение угла угломером, измерение температуры термометром и т.п.

Косвенные — это измерения, при которых значение величины определяют на основании известной зависимости между искомой величиной и величинами, значения которых находят прямыми измерениями.

Примеры косвенных измерений: определение объема тела по прямым измерениям его геометрических размеров, нахождение удельного электрического сопротивления проводника по его сопротивлению, длине и площади поперечного сечения.

Косвенные измерения широко распространены в тех случаях, когда искомую величину невозможно или слишком сложно измерить прямым измерением.

Встречаются случаи, когда величину можно измерить только косвенным путём, например размеры астрономического или внутриатомного порядка.

Совокупные — это такие измерения, при которых значения измеряемых величин определяют по результатам повторных измерений одной или нескольких одноименных величин при различных сочетаниях мер или этих величин. Значение искомой величины определяют решением системы уравнений, составляемых по результатам нескольких прямых измерений.

Примером совокупных измерений является определение массы отдельных гирь набора, т.е. проведение калибровки по известной массе одной из них и по результатам прямых измерений и сравнения масс различных сочетаний гирь.

Совместные — это измерения, двух или нескольких разноименных величин, производимые одновременно, для нахождения функциональной зависимости между ними.

Примерами совместных измерений являются определение длины стержня в зависимости от его температуры или зависимости электрического сопротивления проводника от давления и температуры.

Прямые измерения — основа более сложных измерений, и поэтому целесообразно рассмотреть методы прямых измерений. В соответствии с РМГ 29—99 различают:

1. Метод непосредственной оценки, при котором значение величины определяют непосредственно по отсчетному устройству измерительного прибора, например измерение давления пружинным манометром, массы — на весах, силы электрического тока — амперметром.

2. Метод сравнения с мерой, где измеряемую величину сравнивают с величиной, воспроизводимой мерой. Например, измерение массы на рычажных весах с уравновешиванием гирей; измерение напряжения постоянного тока на компенсаторе сравнением с ЭДС параллельного элемента.

3. Метод дополнения, если значение измеряемой величины дополняется мерой этой же величины с таким расчетом, чтобы на прибор сравнения воздействовала их сумма, равная заранее заданному значению.

4. Дифференциальный метод характеризуется измерением разности между измеряемой величиной и известной величиной, воспроизводимой мерой. Метод позволяет получить результат высокой точности при использовании относительно грубых средств измерения.

5. Нулевой метод аналогичен дифференциальному, но разность между измеряемой величиной и мерой сводится к нулю. При этом нулевой метод имеет то преимущество, что мера может быть во много раз меньше измеряемой величины. Например, неравноплечие весы, где P₁L₁=P₂L₂. В электротехнике — это мосты для измерения индуктивности, емкости, сопротивления. Здесь r₁∙r₂= r_x∙r₃, откуда r_x=r₁∙r₂/r₃. В общем случае совпадение сравниваемых величин регистрируется нуль-индикатором.

6. Метод замещения — метод сравнения с мерой, в которой измеряемую величину замещают известной величиной, воспроизводимой мерой. Например, взвешивание с поочередным помещением измеряемой массы и гирь на одну и ту же чашку весов.

Кроме того, можно выделить нестандартизованные методы:

• метод противопоставления, при котором измеряемая величина и величина, воспроизводимая мерой, одновременно воздействуют на прибор сравнения. Например, измерения массы на равноплечих весах с помещением измеряемой массы и уравновешивающих ее гирь на двух чашках весов;

• метод совпадений, где разность между сравниваемыми величинами измеряют, используя совпадение отметок шкал или периодических сигналов.

Например, при измерении длины штангенциркулем наблюдают совпадение отметок на шкалах штангенциркуля и нониуса; при измерении частоты вращения стробоскопом — метки на вращающемся объекте с моментом вспышек известной частоты.

В литературе иногда встречается название измерений с однократными наблюдениями — обыкновенные измерения, с многократными — статистические. Кроме того, если весь измеряемый параметр фиксируется непосредственно СИ, то это — абсолютный метод, а если СИ фиксирует лишь отклонение параметра от установочного значения, то это относительный (пороговый) метод измерения.

По условиям, определяющим точность результата, измерения делятся на три класса.

1. Измерения максимально возможной точности, достижимой при существующем уровне техники. В этот класс включены все высокоточные измерения и в первую очередь эталонные измерения, связанные с максимально возможной точностью воспроизведения установленных единиц физических величин. Сюда относятся также измерения физических констант, прежде всего универсальных, например измерение абсолютного значения ускорения свободного падения.

2. Контрольно-поверочные измерения, погрешность которых с определенной вероятностью не должна превышать некоторого заданного значения. В этот класс включены измерения, выполняемые лабораториями государственного контроля (надзора) за соблюдением требований технических регламентов, а также состоянием измерительной техники и заводскими измерительными лабораториями. Эти измерения гарантируют погрешность результата с определенной вероятностью, не превышающей некоторого, заранее заданного значения.

3. Технические измерения, в которых погрешность результата определяется характеристиками средств измерений. Примерами технических измерений являются измерения, выполняемые в процессе производства на промышленных предприятиях, в сфере услуг и др.

Метод измерений

Метод измерений — прием или совокупность приемов сравнения измеряемой величины с ее единицей в соответствии с реализованным принципом измерений.

По общим приемам получения результатов измерений различают:

1. прямой метод измерений;
2. косвенный метод измерений.

Первый реализуется при прямом измерении, второй — при косвенном измерении.

В соответствии с РМГ 29-99, к числу основных методов измерений относят метод непосредственной оценки и методы сравнения: дифференциальный, нулевой, замещения и совпадений.

Непосредственный метод — метод измерений, в котором значение величины определяют непосредственно по отсчетному устройству измерительного прибора прямого действия, например измерения силы тока амперметром.

Методы сравнения с мерой — методы, при которых измеряемая величина сравнивается с величиной, воспроизводимой мерой:

• дифференциальный метод характеризуется измерением разности между измеряемой величиной и известной величиной, воспроизводимой мерой. Примером дифференциального метода может служить измерение вольтметром разности двух напряжений, из которых одно известно с большой точностью, а другое представляет собой искомую величину;
• нулевой метод — при котором разность между измеряемой величиной и мерой сводится к нулю. При этом нулевой метод имеет то преимущество, что мера может быть во много раз меньше измеряемой величины, например измерительный мост;
• метод замещения — метод сравнения с мерой, в котором измеренную величину замещают известной величиной, воспроизводимой мерой. Метод замещения применяется при измерении сопротивления с поочередным замещением его из магазина сопротивлений;
• метод совпадений — метод сравнения с мерой, в котором разность между измеряемой величиной и величиной, воспроизводимой мерой, измеряют, используя совпадение отметок шкал или периодических сигналов. Примером использования данного метода может служить измерение частоты наблюдением при помощи осциллографа фигур Лиссажу.

Погрешность измерений

Погрешность измерений – это отклонение результата измерения Хi от действительного значения измеряемой величины Хи, определяется по формуле:

ΔХизм= Хi- Хи,

Где ΔХизм – погрешность измерения.

Для характеристики точности измерения используют относительную погрешность:

δ= (Δ Хизм/ x)*100

где x — среднее арифметическое значение измерений.

По характеру погрешности подразделяются на систематические, случайные и грубые.

К систематическим погрешностям относят погрешности, которые при повторных измерениях остаются постоянными или изменяются по какому- либо закону (например, поверхность на которой установлен измерительный прибор не очень жесткая, надо заменить ее на более жесткую).

Случайные погрешности – это погрешности, принимаемые при повторных измерениях различные, независимые по знаку и величине значения, не подчиняющиеся какой-либо закономерности (например, колебание припуска на обработку, точность установки детали на станок, изменение измерительного усилия крепления детали на станке).

Грубые погрешности – это погрешности, не характерные для технологического процесса или результата, приводящие к явным искажениям результатов измерения (например ошибки неквалифицированного персонала, ошибки при отсчете и при записи). Они сразу видны среди прочих результатов.

Погрешность измерения следует рассматривать, как суммарную погрешность складывающуюся из нескольких составляющих:

• Инструментальная погрешность (погрешность средства измерения) например, износ инструмента, погрешность изготовления инструмента.
• Погрешность меры или образца (разность между номинальным значением меры и действительным значением воспроизводимой ею величины).
• Погрешность измерительного цикла при поэтапном измерении.
• Погрешность, связанная с изменениями температуры окружающей среды и условий измерения (например измерение неостывших деталей).
• Погрешность, связанная с человеком непосредственно выполняющим измерения (например, скорость реакции человека, недостаток опыта) и др.

Виды погрешностей

Абсолютная погрешность – это погрешность, выраженная в единицах измеряемой величины.

Относительная погрешность – это отношение абсолютной погрешности измерения к действительному значению измеряемой величины.

Систематическая погрешность – это погрешность измерения, остающаяся постоянной или закономерно изменяющейся при повторных измерениях одной и той же величины.

Прогрессирующая погрешность – это непредсказуемая погрешность, медленно меняющаяся во времени.

Систематические и прогрессирующие погрешности средств измерений вызываются:

• первые — погрешностью градуировки шкалы или ее небольшим сдвигом;
• вторые — старением элементов средства измерения.

Систематическая погрешность остается постоянной или закономерно изменяющейся при многократных измерениях одной и той же величины. Особенность систематической погрешности состоит в том, что она может быть полностью устранена введением поправок. Особенностью прогрессирующих погрешностей является то, что они могут быть скорректированы только в данный момент времени. Они требуют непрерывной коррекции.

Случайная погрешность – это погрешность измерения изменяется случайным образом. При повторных измерениях одной и той же величины. Случайные погрешности можно обнаружить только при многократных измерениях. В отличии от систематических погрешностей случайные нельзя устранить из результатов измерений.

Инструментальные погрешности — это погрешности, вызываемые особенностями свойств средств измерений. Они возникают вследствие недостаточно высокого качества элементов средств измерений. К данным погрешностям можно отнести изготовление и сборку элементов средств измерений; погрешности из-за трения в механизме прибора, недостаточной жесткости его элементов и деталей и др. Подчеркнем, что инструментальная погрешность индивидуальна для каждого средства измерений.

Методическая погрешность — это погрешность средства измерения, возникающая из-за несовершенства метода измерения, неточности соотношения, используемого для оценки измеряемой величины.

Погрешности средств измерений:

Абсолютная погрешность меры – это разность между номинальным ее значением и истинным (действительным) значением воспроизводимой ею величины

Абсолютная погрешность измерительного прибора – это разность между показанием прибора и истинным (действительным) значением измеряемой величины

Относительная погрешность меры или измерительного прибора – это отношение абсолютной погрешности меры или измерительного прибора к истинному (действительному) значению воспроизводимой или измеряемой величины. Относительная погрешность меры или измерительного прибора может быть выражена в ( % ).

Приведенная погрешность измерительного прибора – отношение погрешности измерительного прибора к нормирующему значению. Нормирующие значение XN – это условно принятое значение, равное или верхнему пределу измерений, или диапазону измерений, или длине шкалы. Приведенная погрешность обычно выражается в ( % ).

Предел допускаемой погрешности средств измерений – наибольшая без учета знака погрешность средства измерений, при которой оно может быть признано и допущено к применению. Данное определение применяют к основной и дополнительной погрешности, а также к вариации показаний. Поскольку свойства средств измерений зависят от внешних условий, их погрешности также зависят от этих условий, поэтому погрешности средств измерений принято делить на основные и дополнительные:

• Основная – это погрешность средства измерений, используемого в нормальных условиях, которые обычно определены в нормативно-технических документах на данное средство измерений.
• Дополнительная – это изменение погрешности средства измерений вследствии отклонения влияющих величин от нормальных значений.

Погрешности средств измерений подразделяются также на статические и динамические.

Статическая – это погрешность средства измерений, используемого для измерения постоянной величины. Если измеряемая величина является функцией времени, то вследствие инерционности средств измерений возникает составляющая общей погрешности, называется динамической погрешностью средств измерений.

Также существуют систематические и случайные погрешности средств измерений они аналогичны с такими же погрешностями измерений.

Факторы влияющие на погрешность измерений

Погрешности возникают по разным причинам: это могут быть ошибки экспериментатора или ошибки из-за применения прибора не по назначению и т.д. Существует ряд понятий которые определяют факторы влияющие на погрешность измерений.

Вариация показаний прибора – это наибольшая разность показаний полученных при прямом и обратном ходе при одном и том же действительном значении измеряемой величины и неизменных внешних условиях.

Класс точности прибора – это обобщенная характеристика средств измерений (прибора), определяемая пределами допускаемых основной и дополнительных погрешностей, а также другими свойствами средств измерений, влияющих на точность, значение которой устанавливаются на отдельные виды средств измерений.

Классы точности прибора устанавливают при выпуске, градуируя его по образцовому прибору в нормальных условиях.

Прецизионность — показывает, как точно или отчетливо можно произвести отсчет. Она определяется, тем насколько близки друг к другу результаты двух идентичных измерений.

Разрешение прибора — это наименьшее изменение измеряемого значения, на которое прибор будет реагировать.

Диапазон прибора — определяется минимальным и максимальным значением входного сигнала, для которого он предназначен.

Полоса пропускания прибора — это разность между минимальной и максимальной частотой, для которых он предназначен.

Чувствительность прибора — определяется, как отношение выходного сигнала или показания прибора к входному сигналу или измеряемой величине.

Шумы — любой сигнал не несущий полезной информации.

Заключение

В заключение описанного деления погрешностей средств и результатов измерений на случайную, прогрессирующую и систематическую составляющие необходимо обратить внимание на то, что такое деление является весьма упрощенным приемом их анализа. Поэтому всегда следует помнить, что в реальной действительности эти составляющие погрешности проявляются совместно и образуют единый нестационарный случайный процесс. Погрешность результата измерений при этом можно представить в виде суммы случайных и систематических Dс погрешностей: D = Dс +. В погрешности измерений входит случайная составляющая, поэтому её следует считать случайной величиной.

Рассмотрение характера проявления погрешностей измерений показывает, нам, что единственно правильный путь оценки погрешностей дает нам теория вероятностей и математическая статистика.

Литература

https://revolution.allbest.ru/manufacture/00674086_0.html

http://xn—-etb8afbn2f.xn--p1ai/electrical-measurements/36-metody-izmereniy-i-pogreshnosti-izmereniy.html

Методы измерений, погрешности измерений

https://kipia-portal.ru/2017/10/17/pogreshnost-izmereniya/

https://helpiks.org/7-8093.html

2.1. Погрешности измерений, их классификация

Истинное значение
физической величины
– значение физической величины, которое
идеальным образом отражало бы в
количественном и качественном отношениях
соответствующее свойство объекта.

Результат любого
измерения отличается от истинного
значения физической величины на некоторое
значение, зависящее от точности средств
и методов измерения, квалификации
оператора, условий, в которых проводилось
измерение, и т. д. Отклонение результата
измерения от истинного значения
физической величины называется
погрешностью
измерения.

Поскольку определить
истинное значение физической величины
в принципе невозможно, так как это
потребовало бы применения идеально
точного средства измерений, то на
практике вместо понятия истинного
значения физической величины применяют
понятие действительного
значения измеряемой величины,
которое настолько точно приближается
к истинному значению, что может быть
использовано вместо него. Это может
быть, например, результат измерения
физической величины образцовым средством
измерения.

Абсолютная
погрешность измерения
(Δ) – это разность между результатом
измерения х
и действительным (истинным) значением
физической величины х_и:

Δ
= х –
х_и.
(2.1)

Относительная
погрешность измерения
(δ) – это отношение абсолютной погрешности
к действительному (истинному) значению
измеряемой величины (часто выраженное
в процентах):

δ
= (Δ / х_и)·100 %
(2.2)

Приведенная
погрешность (γ)
– это выраженное в процентах отношение
абсолютной погрешности к нормирующему
значению Х_N
– условно принятому значению физической
величины, постоянному во всем диапазоне
измерений:

γ =
(Δ /Х_N)·100 %
(2.3)

Для приборов с
нулевой отметкой на краю шкалы нормирующее
значение Х_N
равно конечному значению диапазона
измерений. Для приборов с двухсторонней
шкалой, т. е. с отметками шкалы,
расположенными по обе стороны от нуля
значение Х_N
равно арифметической сумме модулей
конечных значений диапазона измерения.

Погрешность
измерения (результирующая
погрешность)
является суммой двух составляющих:
систематической
и случайной
погрешностей.

Систематическая
погрешность
– это составляющая погрешности измерения,
остающаяся постоянной или закономерно
изменяющаяся при повторных измерениях
одной и той же величины. Причинами
появления систематической погрешности
могут являться неисправности средств
измерений, несовершенство метода
измерений, неправильная установка
измерительных приборов, отступление
от нормальных условий их работы,
особенности самого оператора.
Систематические погрешности в принципе
могут быть выявлены и устранены. Для
этого требуется проведение тщательного
анализа возможных источников погрешностей
в каждом конкретном случае.

Систематические
погрешности подразделяются на:

• методические;

• инструментальные;

• субъективные.

Методические
погрешности
происходят от несовершенства метода
измерения, использования упрощающих
предположений и допущений при выводе
применяемых формул, влияния измерительного
прибора на объект измерения. Например,
измерение температуры с помощью термопары
может содержать методическую погрешность,
вызванную нарушением температурного
режима объекта измерения вследствие
внесения термопары.

Инструментальные
погрешности
зависят от погрешностей применяемых
средств измерения. Неточность градуировки,
конструктивные несовершенства, изменения
характеристик прибора в процессе
эксплуатации и т. д. являются причинами
основных погрешностей инструмента
измерения.

Субъективные
погрешности
вызываются неправильными отсчетами
показаний прибора человеком (оператором).
Например, погрешность от параллакса,
вызванная неправильным направлением
взгляда при наблюдении за показаниями
стрелочного прибора. Использование
цифровых приборов и автоматических
методов измерения позволяет исключить
такого рода погрешности.

Во многих случаях
систематическую погрешность в целом
можно представить как сумму двух
составляющих: аддитивной
(∆_а)
и
мультипликативной
(∆_м).

Если реальная
характеристика средства измерения
смещена относительно номинальной так,
что при всех значениях преобразуемой
величины Х
выходная величина Y
оказывается больше (или меньше) на одну
и ту же величину Δ, то такая погрешность
называется аддитивной
погрешностью нуля (рис.
2.1).

Мультипликативная
погрешность
– это погрешность чувствительности
средства измерения.

Такой подход
позволяет легко скомпенсировать влияние
систематической погрешности на результат
измерения путем введения раздельных
поправочных коэффициентов для каждой
из этих двух составляющих.

Рис.
2.1. К пояснению понятий аддитивной

и
мультипликативной погрешностей

Случайная
погрешность (∆_с)
– это составляющая погрешности измерения,
изменяющаяся случайным образом при
повторных измерениях одной и той же
величины. Наличие случайных погрешностей
выявляется при проведении ряда измерений
постоянной физической величины, когда
оказывается, что результаты измерений
не совпадают друг с другом. Часто
случайные погрешности возникают из-за
одновременного действия многих
независимых причин, каждая из которых
в отдельности слабо влияет на результат
измерения.

Во многих случаях
влияние случайных погрешностей можно
уменьшить путем выполнения многократных
измерений с последующей статистической
обработкой полученных результатов.

В некоторых случаях
оказывается, что результат одного
измерения резко отличается от результатов
других измерений, выполненных при тех
же контролируемых условиях. В этом
случае говорят о грубой погрешности
(промахе измерения). Причиной могут
послужить ошибка оператора, возникновение
сильной кратковременной помехи, толчок,
нарушение электрического контакта и
т. д. Такой результат, содержащий
грубую
погрешность
необходимо выявить, исключить и не
учитывать при дальнейшей статистической
обработке результатов измерений.

Причины
возникновения погрешностей измерений

Имеется ряд
слагаемых погрешностей, которые являются
доминирующими в общей погрешности
измерений. К ним относятся:

1. Погрешности,
   зависящие от средств измерений.
   Нормируемую допустимую погрешность
   средства измерения следует рассматривать
   как погрешность измерения при одном
   из возможных вариантов использования
   этого средства
   измерения.

2. Погрешности,
   зависящие от установочных мер.
   Установочные меры могут быть универсальными
   (концевые меры) и специальными
   (изготовленными по виду измеряемой
   детали). Погрешность измерения будет
   меньшее, если установочная мера будет
   максимально подобна измеряемой детали
   о конструкции, массе, материалу, его
   физическим свойствам, способу базирования
   и т. д. Погрешности от концевых мер длины
   возникают из-за погрешности изготовления
   или погрешности аттестации, а также
   из-за погрешности их притирки.

3. Погрешности,
   зависящие от измерительного усилия.
   При оценке влияния измерительного
   усилия на погрешность измерения
   необходимо выделить упругие деформации
   установочного узла и деформации в зоне
   контакта измерительного наконечника
   с деталью.

4. Погрешности,
   происходящие от температурных деформаций.
   Погрешности возникают из-за разности
   температур объекта измерения и
   измерительного средства. Существует
   два основных источника, обуславливающих
   погрешность от температурных деформаций:
   отклонение температуры воздуха от
   20 °С и кратковременные колебания
   температуры воздуха в процессе измерения.

5. Погрешности,
   зависящие от оператора
   (субъективные погрешности). Возможны
   четыре вида субъективных погрешностей:

• погрешность
  отсчитывания
  (особенно важна, когда обеспечивается
  погрешность измерения, не превышающая
  цену деления);

• погрешность
  присутствия
  (проявляется в виде влияния теплоизлучения
  оператора на температуру окружающей
  среды, а тем самым и на измерительное
  средство);

• погрешность
  действия
  (вносится оператором при настройке
  прибора);

• профессиональные
  погрешности
  (связаны с квалификацией оператора, с
  отношением его к процессу измерения).

1. Погрешности при
   отклонениях от правильной геометрической
   формы.

2. Дополнительные
   погрешности при измерении внутренних
   размеров.

При характеристике
погрешностей средств измерений часто
пользуются

понятием
предела допускаемой погрешности средств
измерений.

Предел допускаемой
погрешности средства измерений
– это наибольшая, без учета знака,
погрешность средства измерений, при
котором оно может быть признано и
допущено к применению. Определение
применимо к основной и дополнительной
погрешности средств измерений.

Учет всех нормируемых
метрологических характеристик средств
измерений является сложной и трудоемкой
процедурой. На практике такая точность
не нужна. Поэтому для средств измерений,
используемых в повседневной практике,
принято деление на классы
точности,
которые дают их обобщенную метрологическую
характеристику.

Требования к
метрологическим характеристикам
устанавливаются в стандартах на средства
измерений конкретного типа.

Классы точности
присваиваются средствам измерений с
учетом результатов государственных
приемочных испытаний.

Класс точности
средства измерений
– обобщенная характеристика средства
измерений, определяемая пределами
допускаемых основных и дополнительных
погрешностей. Класс точности может
выражаться одним числом или дробью
(если аддитивная и мультипликативная
погрешности сопоставимы – например,
0,2/0,05 – адд./мульт.).

Обозначения классов
точности наносятся на циферблаты, щитки
и корпуса средств измерений, приводятся
в нормативно-технических документах.
Классы точности могут обозначаться
буквами (например, М, С и т. д.) или
римскими цифрами (I,
II,
III
и т. д.). Обозначение классов точности
по ГОСТу 8.401-80 может сопровождаться
дополнительными условными знаками:

• 0,5;
  1,6; 2,5 и т. д. – для приборов, приведенная
  погрешность которых составляет 0,5; 1,6;
  2,5 % от нормирующего значения X_N.
  При этом X_N
  принимается равным большему из модулей
  пределов измерений, если нулевое
  значение входного (выходного) сигнала
  находится на краю или вне диапазона
  измерений;

• 0,1,
  0,4, 1,0 и т. д. – для приборов, у которых
  относительная
  погрешность
  составляет 0,1; 0,4; 1,0 % непосредственно
  от полученного значения измеряемой
  величины x;

• 0,02/0,01 – для
  приборов, у которых измеряемая величина
  не может отличаться от значения x,
  показанного указателем, больше, чем на
  [С+d(|X_N/x|-1)]%,
  где C
  и d
  – числитель и знаменатель соответственно
  в обозначении класса точности; X_N
  – больший
  (по модулю) из пределов измерений
  прибора.

Примеры обозначения
классов точности приведены на рис. 2.2.

Рис.
2.2. Лицевые панели приборов:

а
– вольтметра
класса точности 0,5; б
– амперметра
класса точности 1,5;

в
– амперметра
класса точности 0,02/0,01;

г
– мегомметра класса точности 2,5 с
неравномерной шкалой

Метрологическая
надежность средств измерения

В процессе
эксплуатации любого средства измерения
может возникнуть неисправность или
поломка, называемые отказом.

Метрологическая
надежность
средств
измерения
– это свойство средств измерений
сохранять установленные значения
метрологических характеристик в течение
определенного времени при нормальных
режимах и рабочих условиях эксплуатации.
Она характеризуется интенсивностью
отказов, вероятностью безотказной
работы и наработкой на отказ.

Интенсивность
отказов
определяется выражением:

,
(2.1)

где
L
– число отказов; N
– число однотипных элементов; ∆t
– промежуток времени.

Для средств
измерения, состоящего из
n
типов элементов, интенсивность
отказов
рассчитывается как

(2.2)

где
m_i
–
количество элементов i-го
типа.

Вероятность
безотказной работы:

(2.3)

Наработка на
отказ:

(2.4)

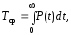
Для внезапного
отказа, интенсивность отказов которого
не зависит от времени работы средства
измерения:

(2.5)

Межповерочный
интервал, в
течение которого обеспечивается заданная
вероятность безотказной работы,
определяется по формуле:

,
(2.6)

где
P_мо
– вероятность метрологического отказа
за время между поверками; P(t)
– вероятность безотказной работы.

В процессе
эксплуатации может производиться
корректировка межповерочного интервала.

Поверка средств
измерения

В основе обеспечения
единообразия средств измерений лежит
система передачи размера единицы
измеряемой величины. Технической формой
надзора за единообразием средств
измерений является государственная
(ведомственная) поверка средств измерений,
устанавливающая их метрологическую
исправность.

Поверка
– определение метрологическим органом
погрешностей средства измерений и
установление его пригодности к применению.

Пригодным к
применению в течение определенного
межповерочного
интервала
времени признают те СИ, поверка которых
подтверждает их соответствие
метрологическим и техническим требованиям
к данному СИ.

Средства измерений
подвергают первичной, периодической,
внеочередной, инспекционной и экспертной
поверкам.

Первичной поверке
подвергаются
СИ при выпуске из производства или
ремонта, а также СИ, поступающие по
импорту.

Периодической
поверке подлежат
СИ, находящиеся в эксплуатации или на
хранении через определенные межповерочные
интервалы, установленные с расчетом
обеспечения пригодности к применению
СИ на период между поверками.

Инспекционную
поверку производят
для выявления пригодности к применению
СИ при осуществлении госнадзора и
ведомственного метрологического
контроля за состоянием и применением
СИ.

Экспертную
поверку выполняют
при возникновении спорных вопросов по
метрологическим характеристикам (MX),
исправности СИ и пригодности их к
применению.

Достоверная
передача размера единиц во всех звеньях
метрологической цепи от эталонов или
от исходного образцового средства
измерений к рабочим средствам измерений
производится в определенном порядке,
приведенном в поверочных схемах.

Поверочная схема
– это утвержденный в установленном
порядке документ, регламентирующий
средства, методы и точность передачи
размера единицы физической величины
от государственного эталона или исходного
образцового средства измерений рабочим
средствам.

Различают
государственные, ведомственные и
локальные поверочные схемы органов
государственной или ведомственных
метрологических служб.

Государственная
поверочная схема
распространяется на все средства
измерений данной ФВ, имеющиеся в стране.
Устанавливая многоступенчатый порядок
передачи размера единицы ФВ от
государственного эталона, требования
к средствам и методам поверки,
государственная поверочная схема
представляет собой структуру
метрологического обеспечения определённого
вида измерений в стране. Эти схемы
разрабатываются главными центрами
эталонов и оформляются одним ГОСТом
ГСИ.

Локальные
поверочные схемы
распространяются на средства измерений,
подлежащие поверке в данном метрологическом
подразделении на предприятии, имеющем
право поверки средств измерений, и
оформляются в виде стандарта предприятия.
Ведомственные и локальные поверочные
схемы не должны противоречить
государственным и должны учитывать их
требования применительно к специфике
конкретного предприятия.

Ведомственная
поверочная схема
разрабатывается органом ведомственной
метрологической службы, согласовывается
с главным центром эталонов – разработчиком
государственной поверочной схемы
средств измерений данной ФВ и
распространяется только на средства
измерений, подлежащие внутриведомственной
поверке.

Поверочная схема
устанавливает передачу размера единиц
одной или нескольких взаимосвязанных
величин. Она должна включать не менее
двух ступеней передачи размера. Поверочную
схему для СИ одной и той же величины,
существенно отличающихся по диапазонам
измерений, условиям применения и методам
поверки, а также для СИ нескольких ФВ
допускается подразделять на части. На
чертежах поверочной схемы должны быть
указаны:

• наименования СИ
  и методов поверки;

• номинальные
  значения ФВ или их диапазоны;

• допускаемые
  значения погрешностей СИ;

• допускаемые
  значения погрешностей методов поверки.
  Правила расчета параметров поверочных
  схем и оформления чертежей поверочных
  схем приведены в ГОСТ 8.061-80 «ГСИ.
  Поверочные схемы. Содержание и построение»
  и в рекомендациях МИ 83-76 «Методика
  определения параметров поверочных
  схем».

Калибровка
средств измерения

Калибровка
средства измерений
– это
совокупность операций, выполняемых
калибровочной лабораторией с целью
определения и подтверждения действительных
значений метрологических характеристик
и (или) пригодности средства измерений
к применению в сферах, не подлежащих
государственному метрологическому
контролю и надзору в соответствии с
установленными требованиями.

Результаты
калибровки средств измерений удостоверяются
калибровочным
знаком,
наносимым на средства измерений, или
сертификатом
о калибровке,
а также записью
в эксплуатационных документах.

Поверку (обязательная
госповерка) может выполнять, как правило,
орган государственной метрологической
службы, а калибровку –
любая
аккредитованная и неаккредитованная
организация.

Поверка обязательна
для средств измерений, применяемых в
сферах, подлежащих государственному
метрологическому контролю (ГМК),
калибровка же –
процедура
добровольная, поскольку относится к
средствам измерений, не подлежащим ГМК.
Предприятие вправе самостоятельно
решать вопрос о выборе форм и режимов
контроля состояния средств измерений,
за исключением тех областей применения
средств измерений, за которыми государства
всего мира устанавливают свой контроль
– это
здравоохранение, безопасность труда,
экология и др.

Освободившись от
государственного контроля, предприятия
попадают под не менее жёсткий контроль
рынка. Это означает, что свобода выбора
предприятия по «метрологическому
поведению» является относительной, все
равно необходимо соблюдать метрологические
правила.

В развитых странах
устанавливает и контролирует исполнение
этих правил негосударственная организация,
именуемая «национальной калибровочной
службой». Эта служба берёт на себя
функции регулирования и разрешения
вопросов, связанных со средствами
измерений, не подпадающими под контроль
государственных метрологических служб.

Желание иметь
конкурентоспособную продукцию побуждает
предприятия иметь измерительные
средства, дающие достоверные результаты.

Внедрение системы
сертификации продукции дополнительно
стимулирует поддержание измерительных
средств на соответствующем уровне. Это
согласуется с требованиями систем
качества, регламентируемыми стандартами
ИСО серии 9000.

Построение
Российской системы калибровки (РСК)
основывается на следующих принципах:

• добровольность
  вступления;

• обязательность
  получения размеров единиц от
  государственных эталонов;

• профессионализм
  и компетентность персонала;

• самоокупаемость
  и самофинансирование.

Основное звено
РСК –
калибровочная
лаборатория. Она представляет собой
самостоятельное предприятие или
подразделение в составе метрологической
службы предприятия, которое может
осуществлять калибровку средств
измерений для собственных нужд или для
сторонних организаций. Если калибровка
проводится для сторонних организаций,
то калибровочная лаборатория должна
быть аккредитована органом РСК.
Аккредитацию осуществляют государственные
научные метрологические центры или
органы Государственной метрологической
службы в соответствии со своей компетенцией
и требованиями, установленными в ГОСТе
51000.2-95 «Общие требования к аккредитующему
органу».

Порядок аккредитации
метрологической службы утвержден
постановлением Госстандарта РФ от 28
декабря 1995 г. № 95 «Порядок аккредитации
метрологических служб юридических лиц
на право проведения калибровочных
работ».

Методы поверки
(калибровки) средств измерения

Допускается
применение четырех методов
поверки
(калибровки) средств измерений:

• непосредственное
  сличение с эталоном;

• сличение с помощью
  компаратора;

• прямые измерения
  величины;

• косвенные измерения
  величины.

Метод
непосредственного сличения
поверяемого (калибруемого) средства
измерения с эталоном соответствующего
разряда широко применяется для различных
средств измерений в таких областях, как
электрические и магнитные измерения,
для определения напряжения, частоты и
силы тока. В основе метода лежит проведение
одновременных измерений одной и той же
физической величины поверяемым
(калибруемым) и эталонным приборами.
При этом определяют погрешность как
разницу показаний поверяемого и
эталонного средств измерений, принимая
показания эталона за действительное
значение величины. Достоинства этого
метода в его простоте, наглядности,
возможности применения автоматической
поверки (калибровки), отсутствии
потребности в сложном оборудовании.

Метод сличения
с помощью компаратора
основан на использовании прибора
сравнения, с помощью которого сличаются
поверяемое (калибруемое) и эталонное
средства измерения. Потребность в
компараторе возникает при невозможности
сравнения показаний приборов, измеряющих
одну и ту же величину, например, двух
вольтметров, один из которых пригоден
для постоянного тока, а другой –
переменного.
В подобных ситуациях в схему поверки
(калибровки) вводится промежуточное
звено –
компаратор.
Для приведенного примера потребуется
потенциометр, который и будет компаратором.
На практике компаратором может служить
любое средство измерения, если оно
одинаково реагирует на сигналы как
поверяемого (калибруемого), так и
эталонного измерительного прибора.
Достоинством данного метода специалисты
считают последовательное во времени
сравнение двух величин.

Метод прямых
измерений
применяется, когда имеется возможность
сличить испытуемый прибор с эталонным
в определенных пределах измерений. В
целом этот метод аналогичен методу
непосредственного сличения, но методом
прямых измерений производится сличение
на всех числовых отметках каждого
диапазона (и поддиапазонов, если они
имеются в приборе). Метод прямых измерений
применяют, например, для поверки или
калибровки вольтметров постоянного
электрического тока.

Метод косвенных
измерений
используется, когда действительные
значения измеряемых величин невозможно
определить прямыми измерениями либо
когда косвенные измерения оказываются
более точными, чем прямые. Этим методом
определяют вначале не искомую
характеристику, а другие, связанные с
ней определенной зависимостью. Искомая
характеристика определяется расчетным
путем. Например, при поверке (калибровке)
вольтметра постоянного тока эталонным
амперметром устанавливают силу тока,
одновременно измеряя сопротивление.
Расчетное значение напряжения сравнивают
с показателями калибруемого (поверяемого)
вольтметра. Метод косвенных измерений
обычно применяют в установках
автоматизированной поверки (калибровки).

Погрешности измерений, представление результатов эксперимента

1. Шкала измерительного прибора
2. Цена деления
3. Виды измерений
4. Погрешность измерений, абсолютная и относительная погрешность
5. Абсолютная погрешность серии измерений
6. Представление результатов эксперимента
7. Задачи

п.1. Шкала измерительного прибора

Шкала – это показывающая часть измерительного прибора, состоящая из упорядоченного ряда отметок со связанной с ними нумерацией. Шкала может располагаться по окружности, дуге или прямой линии.

Примеры шкал различных приборов:

п.2. Цена деления

Цена деления измерительного прибора равна числу единиц измеряемой величины между двумя ближайшими делениями шкалы. Как правило, цена деления указана на маркировке прибора.

Алгоритм определения цены деления
Шаг 1. Найти два ближайшие пронумерованные крупные деления шкалы. Пусть первое значение равно a, второе равно b, b > a.
Шаг 2. Посчитать количество мелких делений шкалы между ними. Пусть это количество равно n.
Шаг 3. Разделить разницу значений крупных делений шкалы на количество отрезков, которые образуются мелкими делениями: $$ triangle=frac{b-a}{n+1} $$ Найденное значение (triangle) и есть цена деления данного прибора.

Пример определения цены деления:

Определим цену деления основной шкалы секундомера. Два ближайших пронумерованных деления на основной шкале:a = 5 c b = 10 cМежду ними находится 4 средних деления, а между каждыми средними делениями еще 4 мелких. Итого: 4+4·5=24 деления. Цена деления: begin{gather*} triangle=frac{b-a}{n+1}\ triangle=frac{10-5}{24+1}=frac15=0,2 c end{gather*}

п.3. Виды измерений

Вид измерений

Определение

Пример

Прямое измерение

Физическую величину измеряют с помощью прибора

Измерение длины бруска линейкой

Косвенное измерение

Физическую величину рассчитывают по формуле, куда подставляют значения величин, полученных с помощью прямых измерений

Определение площади столешницы при измеренной длине и ширине

п.4. Погрешность измерений, абсолютная и относительная погрешность

Погрешность измерений – это отклонение измеренного значения величины от её истинного значения.

Составляющие погрешности измерений

Причины

Инструментальная погрешность

Определяется погрешностью инструментов и приборов, используемых для измерений (принципом действия, точностью шкалы и т.п.)

Погрешность метода

Определяется несовершенством методов и допущениями в методике.

Погрешность теории (модели)

Определяется теоретическими упрощениями, степенью соответствия теоретической модели и реальности.

Погрешность оператора

Определяется субъективным фактором, ошибками экспериментатора.

Инструментальная погрешность измерений принимается равной половине цены деления прибора: $$ d=frac{triangle}{2} $$

Если величина (a_0) — это истинное значение, а (triangle a) — погрешность измерения, результат измерений физической величины записывают в виде (a=a_0pmtriangle a).

Абсолютная погрешность измерения – это модуль разности между измеренным и истинным значением измеряемой величины: $$ triangle a=|a-a_0| $$

Отношение абсолютной погрешности измерения к истинному значению, выраженное в процентах, называют относительной погрешностью измерения: $$ delta=frac{triangle a}{a_0}cdot 100text{%} $$

Относительная погрешность является мерой точности измерения: чем меньше относительная погрешность, тем измерение точнее. По абсолютной погрешности о точности измерения судить нельзя.
На практике абсолютную и относительную погрешности округляют до двух значащих цифр с избытком, т.е. всегда в сторону увеличения.

Значащие цифры – это все верные цифры числа, кроме нулей слева. Результаты измерений записывают только значащими цифрами.

Примеры значащих цифр:
0,403 – три значащих цифры, величина определена с точностью до тысячных.
40,3 – три значащих цифры, величина определена с точностью до десятых.
40,300 – пять значащих цифр, величина определена с точностью до тысячных.

В простейших измерениях инструментальная погрешность прибора является основной.
В таких случаях физическую величину измеряют один раз, полученное значение берут в качестве истинного, а абсолютную погрешность считают равной инструментальной погрешности прибора.
Примеры измерений с абсолютной погрешностью равной инструментальной:

• определение длины с помощью линейки или мерной ленты;
• определение объема с помощью мензурки.

Пример получения результатов прямых измерений с помощью линейки:

Измерим длину бруска линейкой, у которой пронумерованы сантиметры и есть только одно деление между пронумерованными делениями. Цена деления такой линейки: begin{gather*} triangle=frac{b-a}{n+1}= frac{1 text{см}}{1+1}=0,5 text{см} end{gather*} Инструментальная погрешность: begin{gather*} d=frac{triangle}{2}=frac{0,5}{2}=0,25 text{см} end{gather*} Истинное значение: (L_0=4 text{см}) Результат измерений: $$ L=L_0pm d=(4,00pm 0,25) text{см} $$ Относительная погрешность: $$ delta=frac{0,25}{4,00}cdot 100text{%}=6,25text{%}approx 6,3text{%} $$

Теперь возьмем линейку с n=9 мелкими делениями между пронумерованными делениями. Цена деления такой линейки: begin{gather*} triangle=frac{b-a}{n+1}= frac{1 text{см}}{9+1}=0,1 text{см} end{gather*} Инструментальная погрешность: begin{gather*} d=frac{triangle}{2}=frac{0,1}{2}=0,05 text{см} end{gather*} Истинное значение: (L_0=4,15 text{см}) Результат измерений: $$ L=L_0pm d=(4,15pm 0,05) text{см} $$ Относительная погрешность: $$ delta=frac{0,05}{4,15}cdot 100text{%}approx 1,2text{%} $$

Второе измерение точнее, т.к. его относительная погрешность меньше.

п.5. Абсолютная погрешность серии измерений

Измерение длины с помощью линейки (или объема с помощью мензурки) являются теми редкими случаями, когда для определения истинного значения достаточно одного измерения, а абсолютная погрешность сразу берется равной инструментальной погрешности, т.е. половине цены деления линейки (или мензурки).

Гораздо чаще погрешность метода или погрешность оператора оказываются заметно больше инструментальной погрешности. В таких случаях значение измеренной физической величины каждый раз немного меняется, и для оценки истинного значения и абсолютной погрешности нужна серия измерений и вычисление средних значений.

Алгоритм определения истинного значения и абсолютной погрешности в серии измерений
Шаг 1. Проводим серию из (N) измерений, в каждом из которых получаем значение величины (x_1,x_2,…,x_N)
Шаг 2. Истинное значение величины принимаем равным среднему арифметическому всех измерений: $$ x_0=x_{cp}=frac{x_1+x_2+…+x_N}{N} $$ Шаг 3. Находим абсолютные отклонения от истинного значения для каждого измерения: $$ triangle_1=|x_0-x_1|, triangle_2=|x_0-x_2|, …, triangle_N=|x_0-x_N| $$ Шаг 4. Находим среднее арифметическое всех абсолютных отклонений: $$ triangle_{cp}=frac{triangle_1+triangle_2+…+triangle_N}{N} $$ Шаг 5. Сравниваем полученную величину (triangle_{cp}) c инструментальной погрешностью прибора d (половина цены деления). Большую из этих двух величин принимаем за абсолютную погрешность: $$ triangle x=maxleft{triangle_{cp}; dright} $$ Шаг 6. Записываем результат серии измерений: (x=x_0pmtriangle x).

Пример расчета истинного значения и погрешности для серии прямых измерений:
Пусть при измерении массы шарика с помощью рычажных весов мы получили в трех опытах следующие значения: 99,8 г; 101,2 г; 100,3 г.
Инструментальная погрешность весов d = 0,05 г.
Найдем истинное значение массы и абсолютную погрешность.

Составим расчетную таблицу:

№ опыта	1	2	3	Сумма
Масса, г	99,8	101,2	100,3	301,3
Абсолютное отклонение, г	0,6	0,8	0,1	1,5

Сначала находим среднее значение всех измерений: begin{gather*} m_0=frac{99,8+101,2+100,3}{3}=frac{301,3}{3}approx 100,4 text{г} end{gather*} Это среднее значение принимаем за истинное значение массы.
Затем считаем абсолютное отклонение каждого опыта как модуль разности (m_0) и измерения. begin{gather*} triangle_1=|100,4-99,8|=0,6\ triangle_2=|100,4-101,2|=0,8\ triangle_3=|100,4-100,3|=0,1 end{gather*} Находим среднее абсолютное отклонение: begin{gather*} triangle_{cp}=frac{0,6+0,8+0,1}{3}=frac{1,5}{3}=0,5 text{(г)} end{gather*} Мы видим, что полученное значение (triangle_{cp}) больше инструментальной погрешности d.
Поэтому абсолютная погрешность измерения массы: begin{gather*} triangle m=maxleft{triangle_{cp}; dright}=maxleft{0,5; 0,05right} text{(г)} end{gather*} Записываем результат: begin{gather*} m=m_0pmtriangle m\ m=(100,4pm 0,5) text{(г)} end{gather*} Относительная погрешность (с двумя значащими цифрами): begin{gather*} delta_m=frac{0,5}{100,4}cdot 100text{%}approx 0,050text{%} end{gather*}

п.6. Представление результатов эксперимента

Результат измерения представляется в виде $$ a=a_0pmtriangle a $$ где (a_0) – истинное значение, (triangle a) – абсолютная погрешность измерения.

Как найти результат прямого измерения, мы рассмотрели выше.
Результат косвенного измерения зависит от действий, которые производятся при подстановке в формулу величин, полученных с помощью прямых измерений.

Погрешность суммы и разности
Если (a=a_0+triangle a) и (b=b_0+triangle b) – результаты двух прямых измерений, то

• абсолютная погрешность их суммы равна сумме абсолютных погрешностей

$$ triangle (a+b)=triangle a+triangle b $$

• абсолютная погрешность их разности также равна сумме абсолютных погрешностей

$$ triangle (a-b)=triangle a+triangle b $$

Погрешность произведения и частного
Если (a=a_0+triangle a) и (b=b_0+triangle b) – результаты двух прямых измерений, с относительными погрешностями (delta_a=frac{triangle a}{a_0}cdot 100text{%}) и (delta_b=frac{triangle b}{b_0}cdot 100text{%}) соответственно, то:

• относительная погрешность их произведения равна сумме относительных погрешностей

$$ delta_{acdot b}=delta_a+delta_b $$

• относительная погрешность их частного также равна сумме относительных погрешностей

$$ delta_{a/b}=delta_a+delta_b $$

Погрешность степени
Если (a=a_0+triangle a) результат прямого измерения, с относительной погрешностью (delta_a=frac{triangle a}{a_0}cdot 100text{%}), то:

• относительная погрешность квадрата (a^2) равна удвоенной относительной погрешности

$$ delta_{a^2}=2delta_a $$

• относительная погрешность куба (a^3) равна утроенной относительной погрешности

$$ delta_{a^3}=3delta_a $$

• относительная погрешность произвольной натуральной степени (a^n) равна

$$ delta_{a^n}=ndelta_a $$

Вывод этих формул достаточно сложен, но если интересно, его можно найти в Главе 7 справочника по алгебре для 8 класса.

п.7. Задачи

Задача 1. Определите цену деления и объем налитой жидкости для каждой из мензурок. В каком случае измерение наиболее точно; наименее точно?

Составим таблицу для расчета цены деления:

№ мензурки	a, мл	b, мл	n	(triangle=frac{b-a}{n+1}), мл
1	20	40	4	(frac{40-20}{4+1}=4)
2	100	200	4	(frac{200-100}{4+1}=20)
3	15	30	4	(frac{30-15}{4+1}=3)
4	200	400	4	(frac{400-200}{4+1}=40)

Инструментальная точность мензурки равна половине цены деления.
Принимаем инструментальную точность за абсолютную погрешность и измеренное значение объема за истинное.
Составим таблицу для расчета относительной погрешности (оставляем две значащих цифры и округляем с избытком):

№ мензурки	Объем (V_0), мл	Абсолютная погрешность (triangle V=frac{triangle}{2}), мл	Относительная погрешность (delta_V=frac{triangle V}{V_0}cdot 100text{%})
1	68	2	3,0%
2	280	10	3,6%
3	27	1,5	5,6%
4	480	20	4,2%

Наиболее точное измерение в 1-й мензурке, наименее точное – в 3-й мензурке.

Ответ:
Цена деления 4; 20; 3; 40 мл
Объем 68; 280; 27; 480 мл
Самое точное – 1-я мензурка; самое неточное – 3-я мензурка

Задача 2. В двух научных работах указаны два значения измерений одной и той же величины: $$ x_1=(4,0pm 0,1) text{м}, x_2=(4,0pm 0,03) text{м} $$ Какое из этих измерений точней и почему?

Мерой точности является относительная погрешность измерений. Получаем: begin{gather*} delta_1=frac{0,1}{4,0}cdot 100text{%}=2,5text{%}\ delta_2=frac{0,03}{4,0}cdot 100text{%}=0,75text{%} end{gather*} Относительная погрешность второго измерения меньше. Значит, второе измерение точней.
Ответ: (delta_2lt delta_1), второе измерение точней.

Задача 3. Две машины движутся навстречу друг другу со скоростями 54 км/ч и 72 км/ч.
Цена деления спидометра первой машины 10 км/ч, второй машины – 1 км/ч.
Найдите скорость их сближения, абсолютную и относительную погрешность этой величины.

Абсолютная погрешность скорости каждой машины равна инструментальной, т.е. половине деления спидометра: $$ triangle v_1=frac{10}{2}=5 (text{км/ч}), triangle v_2=frac{1}{2}=0,5 (text{км/ч}) $$ Показания каждого из спидометров: $$ v_1=(54pm 5) text{км/ч}, v_2=(72pm 0,5) text{км/ч} $$ Скорость сближения равна сумме скоростей: $$ v_0=v_{10}+v_{20}, v_0=54+72=125 text{км/ч} $$ Для суммы абсолютная погрешность равна сумме абсолютных погрешностей слагаемых. $$ triangle v=triangle v_1+triangle v_2, triangle v=5+0,5=5,5 text{км/ч} $$ Скорость сближения с учетом погрешности равна: $$ v=(126,0pm 5,5) text{км/ч} $$ Относительная погрешность: $$ delta_v=frac{5,5}{126,0}cdot 100text{%}approx 4,4text{%} $$ Ответ: (v=(126,0pm 5,5) text{км/ч}, delta_vapprox 4,4text{%})

Задача 4. Измеренная длина столешницы равна 90,2 см, ширина 60,1 см. Измерения проводились с помощью линейки с ценой деления 0,1 см. Найдите площадь столешницы, абсолютную и относительную погрешность этой величины.

Инструментальная погрешность линейки (d=frac{0,1}{2}=0,05 text{см})
Результаты прямых измерений длины и ширины: $$ a=(90,20pm 0,05) text{см}, b=(60,10pm 0,05) text{см} $$ Относительные погрешности (не забываем про правила округления): begin{gather*} delta_1=frac{0,05}{90,20}cdot 100text{%}approx 0,0554text{%}approx uparrow 0,056text{%}\ delta_2=frac{0,05}{60,10}cdot 100text{%}approx 0,0832text{%}approx uparrow 0,084text{%} end{gather*} Площадь столешницы: $$ S=ab, S=90,2cdot 60,1 = 5421,01 text{см}^2 $$ Для произведения относительная погрешность равна сумме относительных погрешностей слагаемых: $$ delta_S=delta_a+delta_b=0,056text{%}+0,084text{%}=0,140text{%}=0,14text{%} $$ Абсолютная погрешность: begin{gather*} triangle S=Scdot delta_S=5421,01cdot 0,0014=7,59approx 7,6 text{см}^2\ S=(5421,0pm 7,6) text{см}^2 end{gather*} Ответ: (S=(5421,0pm 7,6) text{см}^2, delta_Sapprox 0,14text{%})

Метод непосредственной оценки дает значение измеряемой величины непосредственно по отсчетному устройству измерительного прибора прямого действия. Например, измерение давления пружинным манометром, массы на циферблатных весах, силы электрического тока амперметром и т.д. Точность измерений с помощью этого метода бывает ограниченной, но быстрота процесса измерения делает его незаменимым для практического применения. Наиболее многочисленной группой средство измерений, применяемых для измерения этим методом, являются показывающие, в том числе и стрелочные, приборы (манометры, вольтметры, расходомеры и др.). Измерение с помощью интегрирующего измерительного прибора-счетчика также является методом непосредственной оценки. Этим же методом осуществляют измерения с помощью самопищущих приборов. Однако определение какой-либо величины путем планиметрирования площади, ограниченной записанной кривой, уже не является методом непосредственной оценки и относится к косвенным методам.

          В случае выполнения особо точных измерений применяют метод сравнения с мерой, в котором измеряемую величину сравнивают с величиной, воспроизводимой мерой. Например, измерение массы на рычажных весах с уравновешиванием гирям или измерение напряжения постоянного тока на компенсаторе сравнения с ЭДС нормального элемента.

          Метод сравнения с мерой, в котором измеряемая величина и величина, воспроизводимая мерой, одновременно воздействует на прибор сравнения, с помощью которого устанавливается соотношение между этими величинами, называется методом противопоставления. Например, взвешивание груза на равноплечих весах, когда измеряемая масса определяется как сумма масс гирь, ее уравновешивающих, и показания по шкале весов. Этот метод позволяет уменьшить воздействие на результаты измерений влияющих величин, так как они более или менее равномерно искажают сигналы измерительной информации как в цепи преобразования измеряемой величины, так и в цепи преобразования величины, воспроизводимой мерой.

          Дифференциальный (разностный) метод характеризуется измерением разности между значениями измеряемой и известной (воспроизводимой мерой) величин. Например, измерения путем сравнения с образцовой мерой на компараторе, выполняемые при поверке мер длины. Дифференциальный метод позволяет получать результаты с высокой точностью даже при применении относительно грубых средств для измерения разности. Но осуществлять этот метод возможно только при условии воспроизведения с большой точностью известной величины, значение которой близко к значению измеряемой. Это во многом случаях легче, чем изготовить средство измерений высокой точности.

          Нулевой метод – метод сравнения с мерой, в котором результирующий эффект воздействия величин на прибор сравнения доводят до нуля. Например, измерения электрического сопротивления мостом с полным его уравновешиванием.

         Дифференциальные и нулевые методы нашли очень широкое применение во всех видах измерений: от производственных (в цехах) до сличений эталонов, так как используемые меры (гири, нормальные элементы, катушки и магазины сопротивлений) точнее, чем соответствующие им по стоимости и степени распространения приборы.

          Метод совпадений – этот метод сравнений с мерой, в котором разность между значениями искомой и воспроизводимой мерой величин измеряют, используя совпадения отметок шкал или периодических сигналов. Например, при измерении длины с помощью штангенциркуля с нониусом наблюдают совпадение отметок на шкалах штангенциркуля и нониуса. В производственной практике метод совпадений иногда называют нониусным. Этот метод позволяет существенно увеличить точность сравнения с мерой.

          Метод замещения основан на сравнении с мерой, при котором измеряемую величину замещают известной величиной, воспроизводимой мерой, сохраняя все условия неизменным. Например: взвешивание с поочередным помещением измеряемой массы и гирь на одну и ту же чашку весов; измерение электрического сопротивления резистора путем замены его магазином сопротивлений и подбором значения его сопротивления до получения прежних показаний омметра, моста или другого прибора, обладающего достаточной чувствительностью при любой систематической погрешности, так как отчет берется по мере, а не по прибору. Погрешность измерения определяется в основном погрешностью меры и зоной нечувствительности прибора (ноль — индикатора), а потому весьма мала. Недостатком метода замещения является необходимость применения многозначных мер (магазина мер, батареи нормальных элементов, набора гирь и т.д.).

         Комбинация методов замещения и дифференциального хотя несколько снижает точность, но позволяет использовать меньше наборы мер.