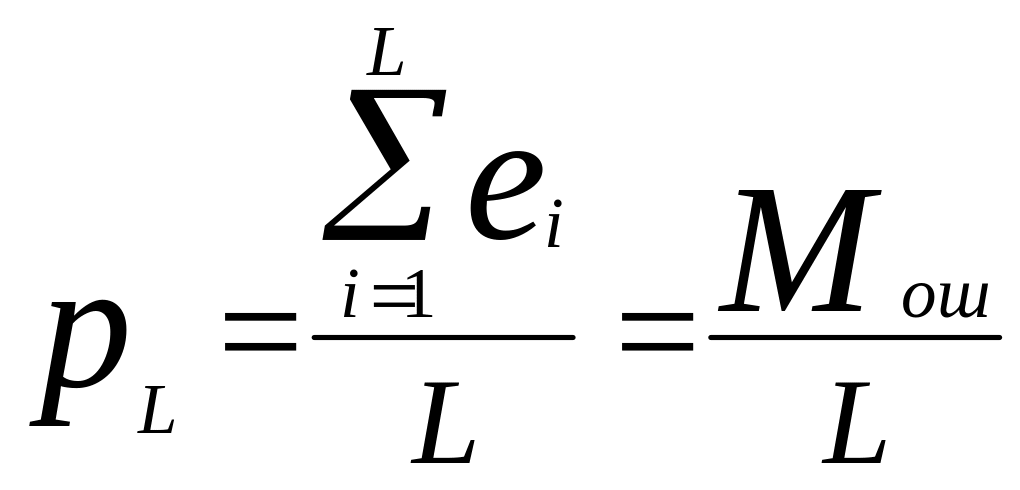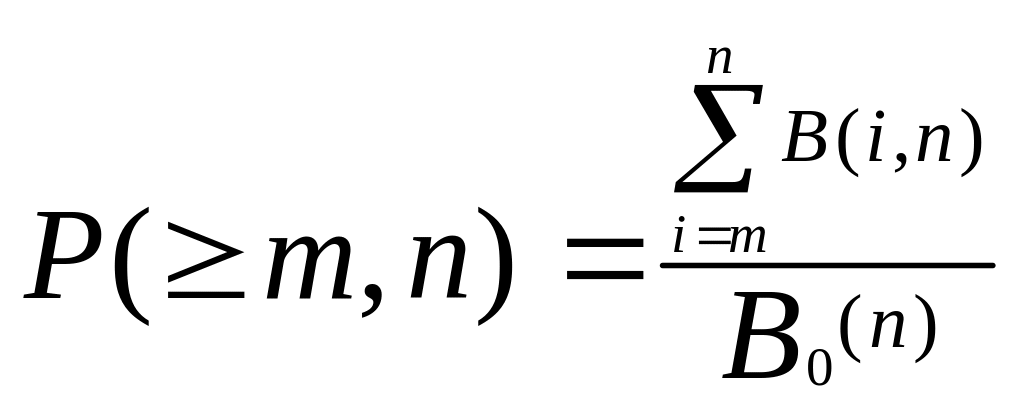Количество ошибок в канале связи

From Wikipedia, the free encyclopedia

In digital transmission, the number of bit errors is the numbers of received bits of a data stream over a communication channel that have been altered due to noise, interference, distortion or bit synchronization errors.

The bit error rate (BER) is the number of bit errors per unit time. The bit error ratio (also BER) is the number of bit errors divided by the total number of transferred bits during a studied time interval. Bit error ratio is a unitless performance measure, often expressed as a percentage.^[1]

The bit error probability p_e is the expected value of the bit error ratio. The bit error ratio can be considered as an approximate estimate of the bit error probability. This estimate is accurate for a long time interval and a high number of bit errors.

Example[edit]

As an example, assume this transmitted bit sequence:

1 1 0 0 0 1 0 1 1

and the following received bit sequence:

0 1 0 1 0 1 0 0 1,

The number of bit errors (the underlined bits) is, in this case, 3. The BER is 3 incorrect bits divided by 9 transferred bits, resulting in a BER of 0.333 or 33.3%.

Packet error ratio[edit]

The packet error ratio (PER) is the number of incorrectly received data packets divided by the total number of received packets. A packet is declared incorrect if at least one bit is erroneous. The expectation value of the PER is denoted packet error probability p_p, which for a data packet length of N bits can be expressed as

,

assuming that the bit errors are independent of each other. For small bit error probabilities and large data packets, this is approximately

Similar measurements can be carried out for the transmission of frames, blocks, or symbols.

The above expression can be rearranged to express the corresponding BER (p_e) as a function of the PER (p_p) and the data packet length N in bits:

Factors affecting the BER[edit]

In a communication system, the receiver side BER may be affected by transmission channel noise, interference, distortion, bit synchronization problems, attenuation, wireless multipath fading, etc.

The BER may be improved by choosing a strong signal strength (unless this causes cross-talk and more bit errors), by choosing a slow and robust modulation scheme or line coding scheme, and by applying channel coding schemes such as redundant forward error correction codes.

The transmission BER is the number of detected bits that are incorrect before error correction, divided by the total number of transferred bits (including redundant error codes). The information BER, approximately equal to the decoding error probability, is the number of decoded bits that remain incorrect after the error correction, divided by the total number of decoded bits (the useful information). Normally the transmission BER is larger than the information BER. The information BER is affected by the strength of the forward error correction code.

Analysis of the BER[edit]

The BER may be evaluated using stochastic (Monte Carlo) computer simulations. If a simple transmission channel model and data source model is assumed, the BER may also be calculated analytically. An example of such a data source model is the Bernoulli source.

Examples of simple channel models used in information theory are:

• Binary symmetric channel (used in analysis of decoding error probability in case of non-bursty bit errors on the transmission channel)
• Additive white Gaussian noise (AWGN) channel without fading.

A worst-case scenario is a completely random channel, where noise totally dominates over the useful signal. This results in a transmission BER of 50% (provided that a Bernoulli binary data source and a binary symmetrical channel are assumed, see below).

In a noisy channel, the BER is often expressed as a function of the normalized carrier-to-noise ratio measure denoted Eb/N0, (energy per bit to noise power spectral density ratio), or Es/N0 (energy per modulation symbol to noise spectral density).

For example, in the case of QPSK modulation and AWGN channel, the BER as function of the Eb/N0 is given by:
.^[2]

People usually plot the BER curves to describe the performance of a digital communication system. In optical communication, BER(dB) vs. Received Power(dBm) is usually used; while in wireless communication, BER(dB) vs. SNR(dB) is used.

Measuring the bit error ratio helps people choose the appropriate forward error correction codes. Since most such codes correct only bit-flips, but not bit-insertions or bit-deletions, the Hamming distance metric is the appropriate way to measure the number of bit errors. Many FEC coders also continuously measure the current BER.

A more general way of measuring the number of bit errors is the Levenshtein distance.
The Levenshtein distance measurement is more appropriate for measuring raw channel performance before frame synchronization, and when using error correction codes designed to correct bit-insertions and bit-deletions, such as Marker Codes and Watermark Codes.^[3]

Mathematical draft[edit]

The BER is the likelihood of a bit misinterpretation due to electrical noise . Considering a bipolar NRZ transmission, we have

for a «1» and for a «0». Each of and has a period of .

Knowing that the noise has a bilateral spectral density ,

is

and is .

Returning to BER, we have the likelihood of a bit misinterpretation .

and

where is the threshold of decision, set to 0 when .

We can use the average energy of the signal to find the final expression :

±§

Bit error rate test[edit]

BERT or bit error rate test is a testing method for digital communication circuits that uses predetermined stress patterns consisting of a sequence of logical ones and zeros generated by a test pattern generator.

A BERT typically consists of a test pattern generator and a receiver that can be set to the same pattern. They can be used in pairs, with one at either end of a transmission link, or singularly at one end with a loopback at the remote end. BERTs are typically stand-alone specialised instruments, but can be personal computer–based. In use, the number of errors, if any, are counted and presented as a ratio such as 1 in 1,000,000, or 1 in 1e06.

Common types of BERT stress patterns[edit]

• PRBS (pseudorandom binary sequence) – A pseudorandom binary sequencer of N Bits. These pattern sequences are used to measure jitter and eye mask of TX-Data in electrical and optical data links.
• QRSS (quasi random signal source) – A pseudorandom binary sequencer which generates every combination of a 20-bit word, repeats every 1,048,575 words, and suppresses consecutive zeros to no more than 14. It contains high-density sequences, low-density sequences, and sequences that change from low to high and vice versa. This pattern is also the standard pattern used to measure jitter.
• 3 in 24 – Pattern contains the longest string of consecutive zeros (15) with the lowest ones density (12.5%). This pattern simultaneously stresses minimum ones density and the maximum number of consecutive zeros. The D4 frame format of 3 in 24 may cause a D4 yellow alarm for frame circuits depending on the alignment of one bits to a frame.
• 1:7 – Also referred to as 1 in 8. It has only a single one in an eight-bit repeating sequence. This pattern stresses the minimum ones density of 12.5% and should be used when testing facilities set for B8ZS coding as the 3 in 24 pattern increases to 29.5% when converted to B8ZS.
• Min/max – Pattern rapid sequence changes from low density to high density. Most useful when stressing the repeater’s ALBO feature.
• All ones (or mark) – A pattern composed of ones only. This pattern causes the repeater to consume the maximum amount of power. If DC to the repeater is regulated properly, the repeater will have no trouble transmitting the long ones sequence. This pattern should be used when measuring span power regulation. An unframed all ones pattern is used to indicate an AIS (also known as a blue alarm).
• All zeros – A pattern composed of zeros only. It is effective in finding equipment misoptioned for AMI, such as fiber/radio multiplex low-speed inputs.
• Alternating 0s and 1s — A pattern composed of alternating ones and zeroes.
• 2 in 8 – Pattern contains a maximum of four consecutive zeros. It will not invoke a B8ZS sequence because eight consecutive zeros are required to cause a B8ZS substitution. The pattern is effective in finding equipment misoptioned for B8ZS.
• Bridgetap — Bridge taps within a span can be detected by employing a number of test patterns with a variety of ones and zeros densities. This test generates 21 test patterns and runs for 15 minutes. If a signal error occurs, the span may have one or more bridge taps. This pattern is only effective for T1 spans that transmit the signal raw. Modulation used in HDSL spans negates the bridgetap patterns’ ability to uncover bridge taps.
• Multipat — This test generates five commonly used test patterns to allow DS1 span testing without having to select each test pattern individually. Patterns are: all ones, 1:7, 2 in 8, 3 in 24, and QRSS.
• T1-DALY and 55 OCTET — Each of these patterns contain fifty-five (55), eight bit octets of data in a sequence that changes rapidly between low and high density. These patterns are used primarily to stress the ALBO and equalizer circuitry but they will also stress timing recovery. 55 OCTET has fifteen (15) consecutive zeroes and can only be used unframed without violating one’s density requirements. For framed signals, the T1-DALY pattern should be used. Both patterns will force a B8ZS code in circuits optioned for B8ZS.

Bit error rate tester[edit]

A bit error rate tester (BERT), also known as a «bit error ratio tester»^[4] or bit error rate test solution (BERTs) is electronic test equipment used to test the quality of signal transmission of single components or complete systems.

The main building blocks of a BERT are:

• Pattern generator, which transmits a defined test pattern to the DUT or test system
• Error detector connected to the DUT or test system, to count the errors generated by the DUT or test system
• Clock signal generator to synchronize the pattern generator and the error detector
• Digital communication analyser is optional to display the transmitted or received signal
• Electrical-optical converter and optical-electrical converter for testing optical communication signals

See also[edit]

• Burst error
• Error correction code
• Errored second
• Pseudo bit error ratio
• Viterbi Error Rate

References[edit]

 This article incorporates public domain material from Federal Standard 1037C. General Services Administration. (in support of MIL-STD-188).

External links[edit]

• QPSK BER for AWGN channel – online experiment

В сетях Ethernet наиболее распространенными являются следующие типы ошибок.

Короткий кадр — кадр длиной менее 64 байт (после 8-байтной преамбулы) с правильной контрольной последовательностью.

Наиболее вероятная причина появления коротких кадров — неисправная сетевая плата или неправильно сконфигурированный или испорченный сетевой драйвер.

Длинный кадр (long frame) — кадр длиннее 1518 байт.

Длинный кадр может иметь правильную или неправильную контрольную последовательность. В последнем случае такие кадры обычно называют jabber. Фиксация длинных кадров с правильной контрольной последовательностью указывает чаще всего на некорректность работы сетевого драйвера; фиксация ошибок типа jabber — на неисправность активного оборудования или наличие внешних помех.

Ошибки контрольной последовательности (CRC error) — правильно оформленный кадр допустимой длины (от 64 до 1518 байт), но с неверной контрольной последовательностью (ошибка в поле CRC).

Ошибка выравнивания (alignment error) — кадр, содержащий число бит, не кратное числу байт.

Впервые данный термин был введен компанией Fluke с целью дифференциации различий между удаленными коллизиями и шумами в канале связи.

В соответствии с общепринятым стандартом дефакто число ошибок канального уровня не должно превышать 1% от общего числа переданных по сети кадров. Как показывает опыт, эта величина перекрывается только при наличии явных дефектов кабельной системы сети. При этом многие серьезные дефекты активного оборудования, вызывающие многочисленные сбои в работе сети, не проявляются на канальном уровне сети.

Правило 9.1 Прежде чем анализировать ошибки в сети, необходимо выяснить, какие типы ошибок могут быть определены сетевой платой и драйвером платы на компьютере, где работает программный анализатор протоколов.

Работа любого анализатора протоколов основана на том, что сетевая плата и драйвер переводятся в режим приема всех кадров сети (promiscuous mode). В этом режиме сетевая плата принимает все проходящие по сети кадры, а не только широковещательные и адресованные непосредственно к ней, как в обычном режиме. Анализатор протоколов всю информацию о событиях в сети получает именно от драйвера сетевой платы, работающей в режиме приема всех кадров.

Не все сетевые платы и сетевые драйверы предоставляют анализатору протоколов идентичную и полную информацию об ошибках в сети. Сетевые платы 3Com вообще никакой информации об ошибках не выдают. Если установить анализатор протоколов на такую плату, то значения на всех счетчиках ошибок будут нулевыми.

EtherExpress Pro компании Intel сообщают только об ошибках CRC и выравнивания.

Сетевые платы компании SMC предоставляют информацию только о коротких кадрах.

Сетевые карты D-Link (например, DFE-500TX) и Kingstone (например, KNE 100TX) сообщают полную, а при наличии специального драйвера — даже расширенную, информацию об ошибках и коллизиях в сети.

Ряд разработчиков анализаторов протоколов предлагают свои драйверы для наиболее популярных сетевых плат.

Правило 9.2 В пределах одного домена сети (collision domain) тип и число ошибок, фиксируемых анализатором протоколов, зависят от места подключения измерительного прибора.

Другими словами, в пределах сегмента коаксиального кабеля, концентратора или стека концентраторов картина статистики по каналу может зависеть от места подключения измерительного прибора.

Одна и та же помеха может вызвать фиксацию ошибки CRC, блика, удаленной коллизии или вообще не обнаруживаться в зависимости от взаимного расположения источника помех и измерительного прибора

Одна и та же коллизия может фиксироваться как удаленная или поздняя в зависимости от взаимного расположения конфликтующих станций и измерительного прибора. Кадр, содержащий ошибку CRC на одном концентраторе стека, может быть не зафиксирован на другом концентраторе того же самого стека.

Правило 9.3 Для выявления ошибок на канальном уровне сети измерения необходимо проводить на фоне генерации анализатором протоколов собственного трафика.

Генерация трафика позволяет обострить имеющиеся проблемы и создает условия для их проявления. Трафик должен иметь невысокую интенсивность (не более 100 кадров/с) и способствовать образованию коллизий в сети, т. е. содержать короткие (<100 байт) кадры.

При выборе анализатора протоколов или другого диагностического средства внимание следует обратить прежде всего на то, чтобы выбранный инструмент имел встроенную функцию генерации трафика задаваемой интенсивности. Эта функция имеется, в частности, в анализаторах Observer компании Network Instruments и NetXray компании Cinco (ныне Network Associates).

Правило 9.4 Если наблюдаемая статистика зависит от места подключения измерительного прибора, то источник ошибок, скорее всего, находится на физическом уровне данного домена сети (причина — дефекты кабельной системы или шум внешнего источника).

В противном случае источник ошибок расположен на канальном уровне (или выше) или в другом, смежном, домене сети.

Правило 9.5 Если доля ошибок CRC в общем числе ошибок велика, то следует определить длину кадров, содержащих данный тип ошибок.

При большой доле ошибок CRC в общем числе ошибок целесообразно выяснить причину их появления. Для этого ошибочные кадры из серии надо сравнить с аналогичными хорошими кадрами из той же серии. Если ошибочные кадры будут существенно короче хороших, то это, скорее всего, результаты коллизий. Если ошибочные кадры будут практически такой же длины, то причиной искажения, вероятнее всего, является внешняя помеха. Если же испорченные кадры длиннее хороших, то причина кроется, вероятнее всего, в дефектном порту концентратора или коммутатора, которые добавляют в конец кадра «пустые» байты.

Сравнить длину ошибочных и правильных кадров проще всего посредством сбора в буфер анализатора серии кадров с ошибкой CRC.

Правило 9.6 Если сеть диагностируется впервые и в ней наблюдаются проблемы, то не следует ожидать, что в сети дефектен только один компонент.

Наиболее надежным способом локализации дефектов является поочередное отключение подозрительных станций, концентраторов и кабельных трасс, тщательная проверка топологии линий заземления компьютеров (особенно для сетей 10Base2).

Если сбои в сети происходят в непредсказуемые моменты времени, не связанные с активностью пользователей, проверьте уровень шума в кабеле с помощью кабельного сканера. При отсутствии сканера визуально убедитесь, что кабель не проходит вблизи сильных источников электромагнитного излучения: высоковольтных или сильноточных кабелей, люминесцентных ламп, электродвигателей, копировальной техники и т. п.

Правило 9.7 Отсутствие ошибок на канальном уровне еще не гарантирует того, что информация в сети не искажается.

Следствием ошибок нижнего уровня является повторная передача кадров. Благодаря высокой скорости сети Ethernet (особенно Fast Ethernet) и высокой производительности современных компьютеров, ошибки нижнего уровня не оказывает существенного влияния на время реакции ППО. На самом деле, очень редко встречаются случаи, когда ликвидация только ошибок нижних (канального и физического) уровней сети позволяла существенно улучшить время реакции ППО. В основном проблемы были связаны с серьезными дефектами кабельной системы сети.

Значительно большее влияние на работу ППО в сети оказывают такие ошибки, как бесследное исчезновение или искажение информации в сетевых платах, маршрутизаторах или коммутаторах при полном отсутствии информации об ошибках нижних уровней. Здесь употребляется слово «информация», так как в момент искажения данные еще не оформлены в виде кадра. Причина таких дефектов в следующем. Информация искажается (или исчезает) «в недрах» активного оборудования — сетевой платы, маршрутизатора или коммутатора. При этом приемо-передающий блок этого оборудования вычисляет правильную контрольную последовательность (CRC) уже искаженной ранее информации, и корректно оформленный кадр передается по сети. Ошибок в этом случае, естественно, не фиксируется.

Иногда кроме искажения наблюдается исчезновение информации. Чаще всего оно происходит на дешевых сетевых платах или на коммутаторах Ethernet-FDDI. Механизм исчезновения информации в последнем случае понятен В ряде коммутаторов Ethernet-FDDI обратная связь быстрого порта с медленным (или наоборот) отсутствует, в результате другой порт не получает информации о перегруженности входных/выходных буферов быстрого (медленного) порта. В этом случае при интенсивном трафике информация на одном из портов может пропасть.

Если же защита не установлена, то поведение ППО может быть непредсказуемым.

Помимо замены (отключения) подозрительного оборудования выявить такие дефекты можно двумя способами:

1) первый способ заключается в захвате, декодировании и анализе кадров от подозрительной станции, маршрутизатора или коммутатора. Признаком описанного дефекта служит повторная передача пакета IP или IPX, которой не предшествует ошибка нижнего уровня сети. Некоторые анализаторы протоколов и экспертные системы упрощают задачу, выполняя анализ трассы или самостоятельно вычисляя контрольную сумму пакетов.

2) Вторым способом является метод стрессового тестирования сети.

Выводы. Основная задача диагностики канального уровня сети — выявить наличие повышенного числа коллизий и ошибок в сети и найти взаимосвязь между числом ошибок, степенью загруженности канала связи, топологией сети и местом подключения измерительного прибора. Все измерения следует проводить на фоне генерации анализатором протоколов собственного трафика.

Если установлено, что повышенное число ошибок и коллизий не является следствием перегруженности канала связи, то сетевое оборудование, при работе которого наблюдается повышенное число ошибок, следует заменить.

Если не удается выявить взаимосвязи между работой конкретного оборудования и появлением ошибок, то необходимо провести комплексное тестирование кабельной системы, проверьте уровень шума в кабеле, топологию линий заземления компьютеров, качество питающего напряжения.

Ошибки в каналах
связи появляются в результате воздействия
различного рода случайных помех. Поэтому
последовательность ошибок является
случайной последовательностью, а ее
характеристики — случайными величинами.
Основной метод изучения последовательности
ошибок – статистический метод.

Сущность данного
метода заключается в том, что с помощью
специальных приборов производятся
исследования каналов различного типа.
В процессе исследований выявляются и
накапливаются последовательности
ошибок за длительный промежуток времени.
Обработка и обобщение полученных
статистических данных позволяют
установить и изучить закономерности
появления ошибок в каналах связи. Знание
этих закономерностей, в свою очередь,
позволяет научно обоснованно определять
наиболее эффективные меры борьбы с
ошибками.

Для получения
достоверных статистических результатов
объемы выборок последовательности
ошибок должны быть такими, чтобы они
охватывали все характерные состояния
канала. Опытным путем установлено, что
для получения достоверных статистических
данных каналы, образованные проводными,
радиорелейными и тропосферными линиями
связи, должны испытываться в течение
нескольких суток непрерывно, а
коротковолновые радиоканалы — по
нескольку суток в различное время года.
При этих условиях объем выборки может
достигать

и более элементов по каждому каналу.
Испытаниям подвергаются действующие
каналы в обычных условиях эксплуатации.
Первичные характеристики каналов должны
соответствовать установленным нормам
и периодически контролироваться в
процессе испытания.

Сущность общепринятого
метода выявления последовательности
ошибок в дискретном канале заключается
в следующем. На вход канала подается
испытательная двоичная последовательность

(испытательный текст). На выходе
дискретного канала из принятой
последовательности

поэлементно
вычитается

,
в результате чего образуется
последовательность ошибок

.
В том случае, когда необходимо выявить
лишь последовательность модулей ошибок
Е, на выходе дискретного канала
достаточно произвести поэлементное
сложение по модулю 2 последовательностей

и

:

+
=
Е.

Статистическая
структура испытательной последовательности

должна быть достаточно близка к структуре
передаваемой информации. Этому условию
удовлетворяют двоичные последовательности,
вырабатываемые генераторами
последовательности максимальной длины
( ГПМД). Благодаря этому, а также вследствие
простоты реализации ГПМД получили
наибольшее распространение в качестве
генераторов испытательной последовательности

.

В зависимости от
задач статистических измерений ошибки
могут непосредственно подсчитываться
с помощью счетчиков или записываться
на долговременный носитель для последующей
обработки.

3.4.3 Основные закономерности распределения ошибок в реальных каналах связи

A.
Характер распределения ошибок в реальных
каналах

Одним из основных
параметров последовательности ошибок
является частота появления ошибок p_L.
Частость появления ошибок (или просто
частость ошибок) определяется как
отношение числа ошибок М_ош =
,
появившихся за определенный отрезок
времени t , к общему числу переданных
символов L:

При
достаточно большом L частость ошибок
сходится с вероятностью появления
ошибки (вероятность ошибки) p. Значения
p для различных типов каналов приведены
в таблице 3.1.

В
течение длительного времени, когда
отсутствовали статистические данные
реальных каналов связи, предполагалось,
что ошибки в каналах связи появляются
независимо. При таком распределении
ошибок значение i-го элемента
последовательности ошибок Е не зависит
от того, какое значение принимает любой
другой j-й элемент данной последовательности.

Пусть
Р{e_i=1}=p, P{(e_i=1)/(e_j=1)} —
вероятность приема i-го элемента с
ошибкой (e_i=1) при условии, что ошибка
произошла на j-м месте (e_j=1), а
Р{(e_i=1)/(e_j=0)} — вероятность
приема i-го элемента с ошибкой при
условии, что j-й элемент принят правильно.
Ошибки появляются независимо, если
выполняется условие:

Р{(e_i=1)/(e_j=1)}=Р{(e_i=1)/(e_j=0)}=Р{e_i=1}=p

В
противном случае появление ошибок
является зависимым событием.

При
независимых ошибках достаточно знать
значение единственного параметра р,
чтобы определить распределение любой
случайной величины. Для этого достаточно
воспользоваться схемой Бернулли. В
частности, вероятность появления в
n-элементной комбинации ровно i ошибок
P(i,n) определяется биномиальным
распределением:

( 0 ≤ i ≤ n
).

Вероятность
приема комбинации без ошибки P(0,n)=(1 —
p)ⁿ = qⁿ . Следовательно,
вероятность появления искаженной
комбинации, т.е. комбинации, содержащей
хотя бы одну ошибку,

,
при np « 1, P(≥1,n) ≈ np.

Вероятность
появления m и более ошибок в комбинации
длины n:

.

Иногда
(при m<n/2) для вычисления P(≥m,n) удобнее
пользоваться формулой, полученной из
условия, что

:

.

Многочисленные
исследования реальных каналов связи
не подтвердили гипотезу о независимом
характере появления ошибок.

Рис.3.1

Данные исследования
показали, что ошибки появляются группами
(пачками). Частость ошибок во время
появления группы ошибок возрастает и
становится значительно больше вероятности
р. На рисунке 3.1 в
качестве примера, иллюстрирующего
групповой характер появления ошибок,
приведено абсолютное число ошибок,
появляющихся за каждые пять минут суток
в кабельном телефонном канале связи.
Это число определялось по результатам
испытания канала в течение шести суток.
Ошибки, как показано на рисунке 3.1
группируются в определенные промежутки
времени. В ночное время число ошибок в
подавляющем большинстве пятиминутных
сеансов равно нулю или меньше десяти.
В первой половине дня число ошибок за
пятиминутные интервалы редко бывает
равно нулю, а в большинстве превышает
сотни и тысячи ошибок. Испытания
проводились на скорости телеграфирования
N=1200 бод, поэтому L=5·60·1200=3.6·10⁵
элементов. Частость ошибок p_L в
ночное время колеблется в пределах
0÷3·10^-5, а в дневное время — 0÷10^-2.

Таким
образом, появление ошибок в реальных
каналах является зависимым событием,
поэтому схема Бернулли не применима.
Расчеты по формулам, полученным на
основе данной схемы, приводят к
значительным, а во многих важных для
практики случаях и недопустимым
погрешностям. Групповой характер
появления ошибок проявляется во всех
статистических характеристиках
последовательности ошибок. Поэтому для
математического описания этой
последовательности недостаточно знать
один параметр р, а необходимо определить
дополнительные параметры, учитывающие
степень зависимости появления ошибок
в реальных каналах.

Б.Зависимость вероятности появления
искаженной комбинации от длины

Статистическая
вероятность появления искаженной
комбинации определяется как отношение
числа искаженных комбинаций B_ош(n)
к общему числу комбинаций B₀(n),
т.е.

.

Вероятность Р(≥1,n)
является неубывающей функцией n. При
n=1 Р(≥1,n)=р, а при n→∞ вероятность P(≥1,n)
с ростом n зависит от характера
распределения ошибок.

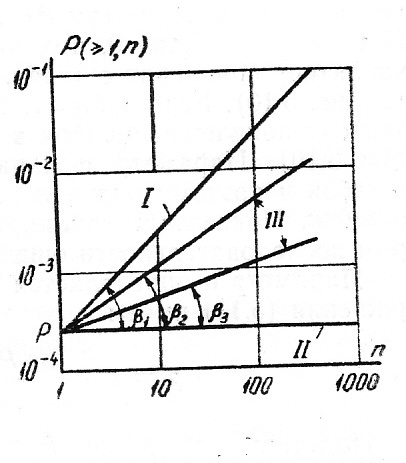
На рис. 3.2 показана
функция P(≥1,n) в логарифмическом масштабе,
т.е. log P(≥1,n)=log
p + log n.
Это выражение является уравнением
прямой, пересекающейся с осью y
точке y=p
под углом β₁. Так как угловой
коэффициент tgβ₁=1,
то β₁=π/4.

Для
гипотетического канала, у которого
часть последовательности ошибок e₁=
e₂=…= e
_Мош=1,
а остальная часть e_Мош+1=
e_Мош+2=…= e_L=0,
на интервале 1≤i≤M_ош
частость ошибок р_L1
= M_ош / M_ош
= 1, а на участке i > M_ош
частость ошибок р_L2=0.
Так как число искаженных комбинаций
длины n B_ош(n)=М_ош
/ n, а общее число
комбинаций B₀ = L
/ n, то вероятность появления
искаженной комбинации:

.

Таким образом, для
канала, у которого ошибки появляются
плотной группой на одном из
временных

и

Рис.
3.2

нтервалов, вероятность появления
искаженной комбинации не зависит от
n и log
Р(≥1,n)=log p.
Это выражение представляет собой
уравнение прямой линии, параллельной
оси абсцисс, так как tg β
= 0 и β = 0 (прямая II
на рис.3.2). Эта прямая пересекается с
осью y в точке с ординатой,
равной р. Прямые I и II
на рис.3.2 являются границами (пределами)
зависимости Р(≥1,n) = f(n),
т.е. p ≤ Р(≥1,n) ≤ np.

Исследования
каналов показали, что для реальных
каналов зависимости log
Р(≥1,n) = f(log
n) достаточно хорошо
аппроксимируются прямыми линиями при
числе элементов в комбинации от 1 до
500. Прямые, соответствующие этим
зависимостям, находятся между указанными
выше границами и имеют угол наклона β
< β₁ (прямые III на
рис.3.2 с углами наклона β₂ и β₃).
Такой характер зависимости Р(≥1,n) = f
(n) является следствием
группового характера появления ошибок
в реальных каналах. Для описания
зависимости Р(≥1,n) = f (n)
достаточно определить значение двух
параметров: вероятности ошибки р и
углового коэффициента tg
β. Обозначим tg
β = 1 – α, тогда

log
Р(≥1,n)
= log p + (1 — α) log n

или

Р(≥1,n) = n^1-α
p .

Если α=0, то tg
β = 1, что соответствует независимому
появлению ошибок. При этом Р(≥1,n) = np
(прямая I на рис.3.16). Если
α = 1, то tg β = 0, что
соответствует предельно групповому
характеру появления ошибок в реальных
каналах (прямые III на
рис.3.2). Параметр α характеризует степень
группирования ошибок и поэтому получил
название показателя группирования
ошибок. Показатель группирования
является важным параметром последовательности
ошибок.

Параметр α
определяется по статистическим данным.
Из выражения для log Р(≥1,n)
имеем:

.

Подставив исходные
значения Р(≥1,n), после преобразования
получим:

.

Для
вычисления параметра α по статистическим
данным последовательность ошибок
разбивают на подпоследовательности
длиной n, определяют число
искаженных комбинаций В_ош(n)
и вычисляют значение α. Однако вычисление
параметра α при одном значении n
может дать значительную погрешность,
так как значения В_ош(n)
на конечной выборке могут иметь случайные
выбросы. Для более точного вычисления
параметра α вычисляют ρ значений α при
ρ значениях n. По полученным
значениям α_i
определяют параметр α как среднее
значение α_i, т.е.

Значения
n берутся из интервала,
где np«1.

При
ρ=5÷10 погрешность вычисления параметра
α становится несущественной.

Значения
параметра α для различных каналов связи
приведены в табл. 3.1

Таблица
3.1

Наибольшее
значение α принимает для телефонных
кабельных каналов, потому что
кратковременные прерывания в различных
промежуточных пунктах кабельной
магистрали приводят к появлению групп
с большой плотностью ошибок.

Меньшее
значение α имеет для радиорелейных
телефонных каналов, так как в них, наряду
с участками большой плотности, наблюдаются
участки с редкими ошибками, появляющимися
за счет повышения уровня шумов.

В
КВ радиотелеграфных каналах вследствие
замирания сигнала и воздействия помех
обычно наблюдаются не только пачки
ошибок, но и одиночные ошибки. Поэтому
показатель группирования принимает,
как правило, наименьшие значения.

Для
каналов тонального телеграфирования
обычно параметр α имеет такое же значение,
что и для кабельных телефонных каналов,
так как причины возникновения ошибок
одни и те же.

В. Распределение
ошибок в комбинациях различной длины

При оценке
эффективности блоковых корректирующих
кодов интерес представляет не только
вероятность появления n-элементных
искаженных комбинаций P(≥1,n),
но и вероятности появления комбинаций
с одной P(1,n),
двумя P(2,n)
и m ошибками P(m,n).

Под
вероятностью появления комбинаций
длины n c m
ошибками будем понимать

.
Очевидно, что:

.

Кроме того, для
оценки эффективности некоторых
корректирующих кодов необходимо знать
суммарную (накопленную) вероятность
появления искаженных комбинаций с m
и более ошибками:

.

Статистическая
вероятность появления n-элементных
комбинаций с m и более
ошибками определяется как отношение
числа комбинаций с m и
боле ошибками к общему числу комбинаций:

,

где В(i,n)
– число n-элементных
комбинаций, содержащих i
ошибок; В₀(n) =

— общее число переданных n-элементных
комбинаций.

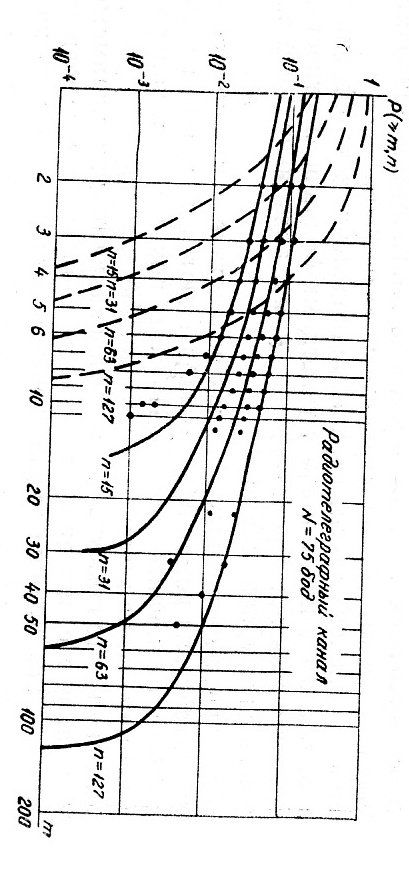
Рис.3.3

На рис. 3.3 в
логарифмическом масштабе показаны
графики Р(≥m,n) для
радиотелеграфного канала с параметрами
р = 1,37 · 10^-2 и α = 0,4. Точками на этом
рисунке нанесены экспериментальные
значения Р(≥m,n), которые
на участке 1≤m≤n/3
достаточно хорошо аппроксимируются
прямыми линиями (сплошные линии).
Исследования зависимости Р(≥m,n)
= f(m) на
реальных каналах показали, что на участке
m<n/3 значения
Р(≥m,n) с ростом m
убывают медленно, что свидетельствует
о наличии искаженных комбинаций с
большим числом ошибок и является
следствием группового характера
появления ошибок в реальных. Скорость
убывания вероятности Р(≥m,n)
с ростом m различна для
различных каналов и определяется
степенью группирования ошибок. Достаточно
хорошая аппроксимация начальной части
зависимости log Р(≥m,n)
= f (log m)
прямыми линиями позволяет получить
приближенную формулу для вычисления
Р(≥m,n) при m<n/3
с использованием параметров p
и α:

На рис. 3.3 для
сравнения пунктирными линиями приведены
зависимости Р(≥m,n) =
f (m),
вычисленные для случая независимых
ошибок при том же значении р = 1.37
·10^-2. В этом случае с увеличением
m вероятности Р(≥m,n)
уменьшаются значительно быстрее, чем
те же вероятности, полученные
экспериментально. Данный пример
показывает, что групповой характер
появления ошибок существенно влияет
на распределение их внутри комбинаций.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Назначение помехоустойчивого кодирования – защита информации от помех и ошибок при передаче и хранении информации. Помехоустойчивое кодирование необходимо для устранения ошибок, которые возникают в процессе передачи, хранения информации. При передачи информации по каналу связи возникают помехи, ошибки и небольшая часть информации теряется. 

Без использования помехоустойчивого кодирования было бы невозможно передавать большие объемы информации (файлы), т.к. в любой системе передачи и хранении информации неизбежно возникают ошибки.

Рассмотрим пример CD диска. Там информация хранится прямо на поверхности диска, в углублениях, из-за того, что все дорожки на поверхности, часто диск хватаем пальцами, елозим по столу и из-за этого без помехоустойчивого кодирования, информацию извлечь не получится.

Использование кодирования позволяет извлекать информацию без потерь даже с поврежденного CD/DVD диска, когда какая либо область становится недоступной для считывания.

В зависимости от того, используется в системе обнаружение или исправление ошибок с помощью помехоустойчивого кода, различают следующие варианты:

• запрос повторной передачи (Automatic Repeat reQuest, ARQ): с помощью помехоустойчивого кода выполняется только обнаружение ошибок, при их наличии производится запрос на повторную передачу пакета данных;
• прямое исправление ошибок (Forward Error Correction, FEC): производится декодирование помехоустойчивого кода, т. е. исправление ошибок с его помощью.

Возможен также гибридный вариант, чтобы лишний раз не гонять информацию по каналу связи, например получили пакет информации, попробовали его исправить, и если не смогли исправить, тогда отправляется запрос на повторную передачу. 

Исправление ошибок в помехоустойчивом кодировании

Любое помехоустойчивое кодирование добавляет избыточность, за счет чего и появляется возможность восстановить информацию при частичной потере данных в канале связи (носителе информации при хранении). В случае эффективного кодирования убирали избыточность, а в помехоустойчивом кодировании добавляется контролируемая избыточность. 

Простейший пример – мажоритарный метод, он же многократная передача, в котором один символ передается многократно, а на приемной стороне принимается решение о том символе, количество которых больше.

Допустим есть 4 символа информации, А, B, С,D, и эту информацию повторяем несколько раз. В процессе передачи информации по каналу связи, где-то возникла ошибка. Есть три пакета (A1B1C1D1|A2B2C2D2|A3B3C3D3), которые должны нести одну и ту же информацию. 

Но из картинки справа, видно, что второй символ (B1 и C1) они отличаются друг от друга, хотя должны были быть одинаковыми. То что они отличаются, говорит о том, что есть ошибка. 

Необходимо найти ошибку с помощью голосования, каких символов больше, символов В или символов С? Явно символов В больше, чем символов С, соответственно принимаем решение, что передавался символ В, а символ С ошибочный. 

Для исправления ошибок нужно, как минимум 3 пакета информации, для обнаружения, как минимум 2 пакета информации.

Параметры помехоустойчивого кодирования

Первый параметр, скорость кода R характеризует долю информационных («полезных») данных в сообщении и определяется выражением: R=k/n=k/m+k

• где n – количество символов закодированного сообщения (результата кодирования);
•   m – количество проверочных символов, добавляемых при кодировании;
•   k – количество информационных символов.

Параметры n и k часто приводят вместе с наименованием кода для его однозначной идентификации. Например, код Хэмминга (7,4) значит, что на вход кодера приходит 4 символа, на выходе 7 символов,  Рида-Соломона (15, 11) и т.д. 

Второй параметр, кратность обнаруживаемых ошибок – количество ошибочных символов, которые код может обнаружить.

Третий параметр, кратность исправляемых ошибок – количество ошибочных символов, которые код может исправить (обозначается буквой t).

Контроль чётности

Самый простой метод помехоустойчивого кодирования это добавление одного бита четности. Есть некое информационное сообщение, состоящее из 8 бит, добавим девятый бит. 

Если нечетное количество единиц, добавляем 0.

1 0 1 0 0 1 0 0 | 0

Если четное количество единиц, добавляем 1.

1 1 0 1 0 1 0 0 | 1

Если принятый бит чётности не совпадает с рассчитанным битом чётности, то считается, что произошла ошибка.

1 1 0 0 0 1 0 0 | 1 

Под кратностью понимается, всевозможные ошибки, которые можно обнаружить. В этом случае, кратность исправляемых ошибок 0, так как мы не можем исправить ошибки, а кратность обнаруживаемых 1. 

Есть последовательность 0 и 1, и из этой последовательности составим прямоугольную матрицу размера 4 на 4. Затем для каждой строки и столбца посчитаем бит четности. 

Прямоугольный код – код с контролем четности, позволяющий исправить одну ошибку:

И если в процессе передачи информации допустим ошибку (ошибка нолик вместо единицы, желтым цветом), начинаем делать проверку. Нашли ошибку во втором столбце, третьей строке по координатам. Чтобы исправить ошибку, просто инвертируем 1 в 0, тем самым ошибка исправляется. 

Этот прямоугольный код исправляет все одно-битные ошибки, но не все двух-битные и трех-битные. 

Рассчитаем скорость кода для: 

• 1 1 0 0 0 1 0 0 | 1 

Здесь R=8/9=0,88

• И для прямоугольного кода:

Здесь R=16/24=0,66 (картинка выше, двадцать пятую единичку (бит четности) не учитываем)

Более эффективный с точки зрения скорости является первый вариант, но зато мы не можем с помощью него исправлять ошибки, а с помощью прямоугольного кода можно. Сейчас на практике прямоугольный код не используется, но логика работы многих помехоустойчивых кодов основана именно на прямоугольном коде. 

Классификация помехоустойчивых кодов

• Непрерывные — процесс кодирования и декодирования носит непрерывный характер. Сверточный код является частным случаем непрерывного кода. На вход кодера поступил один символ, соответственно, появилось несколько на выходе, т.е. на каждый входной символ формируется несколько выходных, так как добавляется избыточность.
• Блочные (Блоковые) — процесс кодирования и декодирования осуществляется по блокам. С точки зрения понимания работы, блочный код проще, разбиваем код на блоки и каждый блок кодируется в отдельности. 

По используемому алфавиту:

• Двоичные. Оперируют битами.
• Не двоичные (код Рида-Соломона). Оперируют более размерными символами. Если изначально информация двоичная, нужно эти биты превратить в символы. Например, есть последовательность 110 110 010 100 и нужно их преобразовать из двоичных символов в не двоичные, берем группы по 3 бита — это будет один символ, 6, 6, 2, 4 — с этими не двоичными символами работают не двоичные помехоустойчивые коды. 

Блочные коды делятся на

• Систематические  — отдельно не измененные информационные символы, отдельно проверочные символы. Если на входе кодера присутствует блок из k символов, и в процессе кодирования сформировали еще какое-то количество проверочных символов и проверочные символы ставим рядом к информационным в конец или в начало. Выходной блок на выходе кодера будет состоять из информационных символов и проверочных. 
• Несистематические — символы исходного сообщения в явном виде не присутствуют. На вход пришел блок k, на выходе получили блок размером n, блок на выходе кодера не будет содержать в себе исходных данных. 

В случае систематических кодов, выходной блок в явном виде содержит в себе, то что пришло на вход, а в случае несистематического кода, глядя на выходной блок нельзя понять что было на входе. 

Смотря на картинку выше, код 1 1 0 0 0 1 0 0 | 1 является систематическим, на вход поступило 8 бит, а на выходе кодера 9 бит, которые в явном виде содержат в себе 8 бит информационных и один проверочный.  

Код Хэмминга

Код Хэмминга — наиболее известный из первых самоконтролирующихся и самокорректирующихся кодов. Позволяет устранить одну ошибку и находить двойную. 

Код Хэмминга (7,4) — 4 бита на входе кодера и 7 на выходе, следовательно 3 проверочных бита. С 1 по 4 информационные биты, с 6 по 7 проверочные (см. табл. выше). Пятый проверочный бит y5, это сумма по модулю два 1-3 информационных бит. Сумма по модулю 2 это вычисление бита чётности. 

Декодирование кода Хэмминга

Декодирование происходит через вычисление синдрома по выражениям:

Синдром это сложение бит по модулю два. Если синдром не нулевой, то исправление ошибки происходит по таблице декодирования:

Расстояние Хэмминга

Расстояние Хэмминга — число позиций, в которых соответствующие символы двух кодовых слов одинаковой длины различны. Если рассматривать два кодовых слова, (пример на картинке ниже, 1 0 1 1 0 0 1 и 1 0 0 1 1 0 1) видно что они отличаются друг от друга на два символа, соответственно расстояние Хэмминга равно 2.

Кратность исправляемых ошибок и обнаруживаемых, связано минимальным расстоянием Хэмминга. Любой помехоустойчивый код добавляет избыточность с целью увеличить минимальное расстояние Хэмминга. Именно минимальное расстояние Хэмминга определяет помехоустойчивость. 

Помехоустойчивые коды

Современные коды более эффективны по сравнению с рассматриваемыми примерами. В таблице ниже приведены Коды Боуза-Чоудхури-Хоквингема (БЧХ)

Из таблицы видим, что там один класс кода БЧХ, но разные параметры n и k. 

• n — количество символов на входе. 
• k — количество символов на выходе. 
• t — кратность исправляемых ошибок. 
• Отношение k/n — скорость кода. 
• G (энергетический выигрыш) — величина, показывающая на сколько можно уменьшить отношение сигнал/шум (Eb/No) для обеспечения заданной вероятности ошибки.

Несмотря на то, что скорость кода близка, количество исправляемых ошибок может быть разное. Количество исправляемых ошибок зависит от той избыточности, которую добавим и от размера блока. Чем больше блок, тем больше ошибок он исправляет, даже при той же самой избыточности. 

Пример: помехоустойчивые коды и двоичная фазовая манипуляция (2-ФМн). На графике зависимость отношения сигнал шум (Eb/No) от вероятности ошибки. За счет применения помехоустойчивых кодов улучшается помехоустойчивость. 

Из графика видим, код Хэмминга (7,4) на сколько увеличилась помехоустойчивость? Всего на пол Дб это мало, если применить код БЧХ (127, 64) выиграем порядка 4 дБ, это хороший показатель. 

Компромиссы при использовании помехоустойчивых кодов

Чем расплачиваемся за помехоустойчивые коды? Добавили избыточность, соответственно эту избыточность тоже нужно передавать. Нужно: увеличивать пропускную способность канала связи, либо увеличивать длительность передачи. 

Компромисс:

1. Достоверность vs полоса пропускания.
2. Мощность vs полоса пропускания.
3. Скорость передачи данных vs полоса пропускания

Необходимость чередования (перемежения)

Все помехоустойчивые коды могут исправлять только ограниченное количество ошибок t. Однако в реальных системах связи часто возникают ситуации сгруппированных ошибок, когда в течение непродолжительного времени количество ошибок превышает t.

Например, в канале связи шумов мало, все передается хорошо, ошибки возникают редко, но вдруг возникла импульсная помеха или замирания, которые повредили на некоторое время процесс передачи, и потерялся большой кусок информации. В среднем на блок приходится одна, две ошибки, а в нашем примере потерялся целый блок, включая информационные и проверочные биты. Сможет ли помехоустойчивый код исправить такую ошибку? Эта проблема решаема за счет перемежения. 

Пример блочного перемежения:

На картинке, всего 5 блоков (с 1 по 25). Код работает исправляя ошибки в рамках одного блока (если в одном блоке 1 ошибка, код его исправит, а если две то нет). В канал связи отдается информация не последовательно, а в перемешку. На выходе кодера сформировались 5 блоков и эти 5 блоков будем отдавать не по очереди а в перемешку. Записали всё по строкам, но считывать будем, чтобы отправлять в канал связи, по столбцам. Информация в блоках перемешалась. В канале связи возникла ошибка и мы потеряли большой кусок. В процессе приема, мы опять составляем таблицу, записываем по столбцам, но считываем по строкам. За счет того, что мы перемешали большое количество блоков между собой, групповая ошибка равномерно распределится по блокам.