«Interleaver» redirects here. For the fiber-optic device, see optical interleaver.
In computing, telecommunication, information theory, and coding theory, forward error correction (FEC) or channel coding[1][2][3] is a technique used for controlling errors in data transmission over unreliable or noisy communication channels.
The central idea is that the sender encodes the message in a redundant way, most often by using an error correction code or error correcting code, (ECC).[4][5] The redundancy allows the receiver not only to detect errors that may occur anywhere in the message, but often to correct a limited number of errors. Therefore a reverse channel to request re-transmission may not be needed. The cost is a fixed, higher forward channel bandwidth.
The American mathematician Richard Hamming pioneered this field in the 1940s and invented the first error-correcting code in 1950: the Hamming (7,4) code.[5]
FEC can be applied in situations where re-transmissions are costly or impossible, such as one-way communication links or when transmitting to multiple receivers in multicast.
Long-latency connections also benefit; in the case of a satellite orbiting Uranus, retransmission due to errors can create a delay of five hours. FEC is widely used in modems and in cellular networks, as well.
FEC processing in a receiver may be applied to a digital bit stream or in the demodulation of a digitally modulated carrier. For the latter, FEC is an integral part of the initial analog-to-digital conversion in the receiver. The Viterbi decoder implements a soft-decision algorithm to demodulate digital data from an analog signal corrupted by noise. Many FEC decoders can also generate a bit-error rate (BER) signal which can be used as feedback to fine-tune the analog receiving electronics.
FEC information is added to mass storage (magnetic, optical and solid state/flash based) devices to enable recovery of corrupted data, and is used as ECC computer memory on systems that require special provisions for reliability.
The maximum proportion of errors or missing bits that can be corrected is determined by the design of the ECC, so different forward error correcting codes are suitable for different conditions. In general, a stronger code induces more redundancy that needs to be transmitted using the available bandwidth, which reduces the effective bit-rate while improving the received effective signal-to-noise ratio. The noisy-channel coding theorem of Claude Shannon can be used to compute the maximum achievable communication bandwidth for a given maximum acceptable error probability. This establishes bounds on the theoretical maximum information transfer rate of a channel with some given base noise level. However, the proof is not constructive, and hence gives no insight of how to build a capacity achieving code. After years of research, some advanced FEC systems like polar code[3] come very close to the theoretical maximum given by the Shannon channel capacity under the hypothesis of an infinite length frame.
How it works[edit]
ECC is accomplished by adding redundancy to the transmitted information using an algorithm. A redundant bit may be a complicated function of many original information bits. The original information may or may not appear literally in the encoded output; codes that include the unmodified input in the output are systematic, while those that do not are non-systematic.
A simplistic example of ECC is to transmit each data bit 3 times, which is known as a (3,1) repetition code. Through a noisy channel, a receiver might see 8 versions of the output, see table below.
| Triplet received | Interpreted as |
|---|---|
| 000 | 0 (error-free) |
| 001 | 0 |
| 010 | 0 |
| 100 | 0 |
| 111 | 1 (error-free) |
| 110 | 1 |
| 101 | 1 |
| 011 | 1 |
This allows an error in any one of the three samples to be corrected by «majority vote», or «democratic voting». The correcting ability of this ECC is:
- Up to 1 bit of triplet in error, or
- up to 2 bits of triplet omitted (cases not shown in table).
Though simple to implement and widely used, this triple modular redundancy is a relatively inefficient ECC. Better ECC codes typically examine the last several tens or even the last several hundreds of previously received bits to determine how to decode the current small handful of bits (typically in groups of 2 to 8 bits).
Averaging noise to reduce errors[edit]
ECC could be said to work by «averaging noise»; since each data bit affects many transmitted symbols, the corruption of some symbols by noise usually allows the original user data to be extracted from the other, uncorrupted received symbols that also depend on the same user data.
- Because of this «risk-pooling» effect, digital communication systems that use ECC tend to work well above a certain minimum signal-to-noise ratio and not at all below it.
- This all-or-nothing tendency – the cliff effect – becomes more pronounced as stronger codes are used that more closely approach the theoretical Shannon limit.
- Interleaving ECC coded data can reduce the all or nothing properties of transmitted ECC codes when the channel errors tend to occur in bursts. However, this method has limits; it is best used on narrowband data.
Most telecommunication systems use a fixed channel code designed to tolerate the expected worst-case bit error rate, and then fail to work at all if the bit error rate is ever worse.
However, some systems adapt to the given channel error conditions: some instances of hybrid automatic repeat-request use a fixed ECC method as long as the ECC can handle the error rate, then switch to ARQ when the error rate gets too high;
adaptive modulation and coding uses a variety of ECC rates, adding more error-correction bits per packet when there are higher error rates in the channel, or taking them out when they are not needed.
Types of ECC[edit]
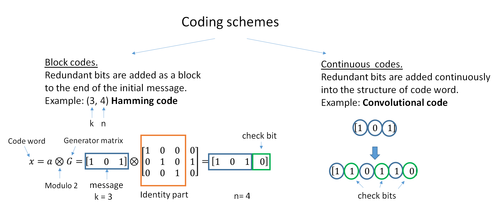
A block code (specifically a Hamming code) where redundant bits are added as a block to the end of the initial message
A continuous code convolutional code where redundant bits are added continuously into the structure of the code word
The two main categories of ECC codes are block codes and convolutional codes.
- Block codes work on fixed-size blocks (packets) of bits or symbols of predetermined size. Practical block codes can generally be hard-decoded in polynomial time to their block length.
- Convolutional codes work on bit or symbol streams of arbitrary length. They are most often soft decoded with the Viterbi algorithm, though other algorithms are sometimes used. Viterbi decoding allows asymptotically optimal decoding efficiency with increasing constraint length of the convolutional code, but at the expense of exponentially increasing complexity. A convolutional code that is terminated is also a ‘block code’ in that it encodes a block of input data, but the block size of a convolutional code is generally arbitrary, while block codes have a fixed size dictated by their algebraic characteristics. Types of termination for convolutional codes include «tail-biting» and «bit-flushing».
There are many types of block codes; Reed–Solomon coding is noteworthy for its widespread use in compact discs, DVDs, and hard disk drives. Other examples of classical block codes include Golay, BCH, Multidimensional parity, and Hamming codes.
Hamming ECC is commonly used to correct NAND flash memory errors.[6]
This provides single-bit error correction and 2-bit error detection.
Hamming codes are only suitable for more reliable single-level cell (SLC) NAND.
Denser multi-level cell (MLC) NAND may use multi-bit correcting ECC such as BCH or Reed–Solomon.[7][8] NOR Flash typically does not use any error correction.[7]
Classical block codes are usually decoded using hard-decision algorithms,[9] which means that for every input and output signal a hard decision is made whether it corresponds to a one or a zero bit. In contrast, convolutional codes are typically decoded using soft-decision algorithms like the Viterbi, MAP or BCJR algorithms, which process (discretized) analog signals, and which allow for much higher error-correction performance than hard-decision decoding.
Nearly all classical block codes apply the algebraic properties of finite fields. Hence classical block codes are often referred to as algebraic codes.
In contrast to classical block codes that often specify an error-detecting or error-correcting ability, many modern block codes such as LDPC codes lack such guarantees. Instead, modern codes are evaluated in terms of their bit error rates.
Most forward error correction codes correct only bit-flips, but not bit-insertions or bit-deletions.
In this setting, the Hamming distance is the appropriate way to measure the bit error rate.
A few forward error correction codes are designed to correct bit-insertions and bit-deletions, such as Marker Codes and Watermark Codes.
The Levenshtein distance is a more appropriate way to measure the bit error rate when using such codes.
[10]
Code-rate and the tradeoff between reliability and data rate[edit]
The fundamental principle of ECC is to add redundant bits in order to help the decoder to find out the true message that was encoded by the transmitter. The code-rate of a given ECC system is defined as the ratio between the number of information bits and the total number of bits (i.e., information plus redundancy bits) in a given communication package. The code-rate is hence a real number. A low code-rate close to zero implies a strong code that uses many redundant bits to achieve a good performance, while a large code-rate close to 1 implies a weak code.
The redundant bits that protect the information have to be transferred using the same communication resources that they are trying to protect. This causes a fundamental tradeoff between reliability and data rate.[11] In one extreme, a strong code (with low code-rate) can induce an important increase in the receiver SNR (signal-to-noise-ratio) decreasing the bit error rate, at the cost of reducing the effective data rate. On the other extreme, not using any ECC (i.e., a code-rate equal to 1) uses the full channel for information transfer purposes, at the cost of leaving the bits without any additional protection.
One interesting question is the following: how efficient in terms of information transfer can an ECC be that has a negligible decoding error rate? This question was answered by Claude Shannon with his second theorem, which says that the channel capacity is the maximum bit rate achievable by any ECC whose error rate tends to zero:[12] His proof relies on Gaussian random coding, which is not suitable to real-world applications. The upper bound given by Shannon’s work inspired a long journey in designing ECCs that can come close to the ultimate performance boundary. Various codes today can attain almost the Shannon limit. However, capacity achieving ECCs are usually extremely complex to implement.
The most popular ECCs have a trade-off between performance and computational complexity. Usually, their parameters give a range of possible code rates, which can be optimized depending on the scenario. Usually, this optimization is done in order to achieve a low decoding error probability while minimizing the impact to the data rate. Another criterion for optimizing the code rate is to balance low error rate and retransmissions number in order to the energy cost of the communication.[13]
Concatenated ECC codes for improved performance[edit]
Classical (algebraic) block codes and convolutional codes are frequently combined in concatenated coding schemes in which a short constraint-length Viterbi-decoded convolutional code does most of the work and a block code (usually Reed–Solomon) with larger symbol size and block length «mops up» any errors made by the convolutional decoder. Single pass decoding with this family of error correction codes can yield very low error rates, but for long range transmission conditions (like deep space) iterative decoding is recommended.
Concatenated codes have been standard practice in satellite and deep space communications since Voyager 2 first used the technique in its 1986 encounter with Uranus. The Galileo craft used iterative concatenated codes to compensate for the very high error rate conditions caused by having a failed antenna.
Low-density parity-check (LDPC)[edit]
Low-density parity-check (LDPC) codes are a class of highly efficient linear block
codes made from many single parity check (SPC) codes. They can provide performance very close to the channel capacity (the theoretical maximum) using an iterated soft-decision decoding approach, at linear time complexity in terms of their block length. Practical implementations rely heavily on decoding the constituent SPC codes in parallel.
LDPC codes were first introduced by Robert G. Gallager in his PhD thesis in 1960,
but due to the computational effort in implementing encoder and decoder and the introduction of Reed–Solomon codes,
they were mostly ignored until the 1990s.
LDPC codes are now used in many recent high-speed communication standards, such as DVB-S2 (Digital Video Broadcasting – Satellite – Second Generation), WiMAX (IEEE 802.16e standard for microwave communications), High-Speed Wireless LAN (IEEE 802.11n),[14] 10GBase-T Ethernet (802.3an) and G.hn/G.9960 (ITU-T Standard for networking over power lines, phone lines and coaxial cable). Other LDPC codes are standardized for wireless communication standards within 3GPP MBMS (see fountain codes).
Turbo codes[edit]
Turbo coding is an iterated soft-decoding scheme that combines two or more relatively simple convolutional codes and an interleaver to produce a block code that can perform to within a fraction of a decibel of the Shannon limit. Predating LDPC codes in terms of practical application, they now provide similar performance.
One of the earliest commercial applications of turbo coding was the CDMA2000 1x (TIA IS-2000) digital cellular technology developed by Qualcomm and sold by Verizon Wireless, Sprint, and other carriers. It is also used for the evolution of CDMA2000 1x specifically for Internet access, 1xEV-DO (TIA IS-856). Like 1x, EV-DO was developed by Qualcomm, and is sold by Verizon Wireless, Sprint, and other carriers (Verizon’s marketing name for 1xEV-DO is Broadband Access, Sprint’s consumer and business marketing names for 1xEV-DO are Power Vision and Mobile Broadband, respectively).
Local decoding and testing of codes[edit]
Sometimes it is only necessary to decode single bits of the message, or to check whether a given signal is a codeword, and do so without looking at the entire signal. This can make sense in a streaming setting, where codewords are too large to be classically decoded fast enough and where only a few bits of the message are of interest for now. Also such codes have become an important tool in computational complexity theory, e.g., for the design of probabilistically checkable proofs.
Locally decodable codes are error-correcting codes for which single bits of the message can be probabilistically recovered by only looking at a small (say constant) number of positions of a codeword, even after the codeword has been corrupted at some constant fraction of positions. Locally testable codes are error-correcting codes for which it can be checked probabilistically whether a signal is close to a codeword by only looking at a small number of positions of the signal.
Interleaving[edit]
«Interleaver» redirects here. For the fiber-optic device, see optical interleaver.
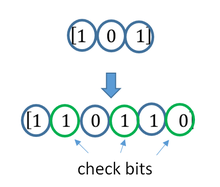
A short illustration of interleaving idea
Interleaving is frequently used in digital communication and storage systems to improve the performance of forward error correcting codes. Many communication channels are not memoryless: errors typically occur in bursts rather than independently. If the number of errors within a code word exceeds the error-correcting code’s capability, it fails to recover the original code word. Interleaving alleviates this problem by shuffling source symbols across several code words, thereby creating a more uniform distribution of errors.[15] Therefore, interleaving is widely used for burst error-correction.
The analysis of modern iterated codes, like turbo codes and LDPC codes, typically assumes an independent distribution of errors.[16] Systems using LDPC codes therefore typically employ additional interleaving across the symbols within a code word.[17]
For turbo codes, an interleaver is an integral component and its proper design is crucial for good performance.[15][18] The iterative decoding algorithm works best when there are not short cycles in the factor graph that represents the decoder; the interleaver is chosen to avoid short cycles.
Interleaver designs include:
- rectangular (or uniform) interleavers (similar to the method using skip factors described above)
- convolutional interleavers
- random interleavers (where the interleaver is a known random permutation)
- S-random interleaver (where the interleaver is a known random permutation with the constraint that no input symbols within distance S appear within a distance of S in the output).[19]
- a contention-free quadratic permutation polynomial (QPP).[20] An example of use is in the 3GPP Long Term Evolution mobile telecommunication standard.[21]
In multi-carrier communication systems, interleaving across carriers may be employed to provide frequency diversity, e.g., to mitigate frequency-selective fading or narrowband interference.[22]
Example[edit]
Transmission without interleaving:
Error-free message: aaaabbbbccccddddeeeeffffgggg Transmission with a burst error: aaaabbbbccc____deeeeffffgggg
Here, each group of the same letter represents a 4-bit one-bit error-correcting codeword. The codeword cccc is altered in one bit and can be corrected, but the codeword dddd is altered in three bits, so either it cannot be decoded at all or it might be decoded incorrectly.
With interleaving:
Error-free code words: aaaabbbbccccddddeeeeffffgggg Interleaved: abcdefgabcdefgabcdefgabcdefg Transmission with a burst error: abcdefgabcd____bcdefgabcdefg Received code words after deinterleaving: aa_abbbbccccdddde_eef_ffg_gg
In each of the codewords «aaaa», «eeee», «ffff», and «gggg», only one bit is altered, so one-bit error-correcting code will decode everything correctly.
Transmission without interleaving:
Original transmitted sentence: ThisIsAnExampleOfInterleaving Received sentence with a burst error: ThisIs______pleOfInterleaving
The term «AnExample» ends up mostly unintelligible and difficult to correct.
With interleaving:
Transmitted sentence: ThisIsAnExampleOfInterleaving... Error-free transmission: TIEpfeaghsxlIrv.iAaenli.snmOten. Received sentence with a burst error: TIEpfe______Irv.iAaenli.snmOten. Received sentence after deinterleaving: T_isI_AnE_amp_eOfInterle_vin_...
No word is completely lost and the missing letters can be recovered with minimal guesswork.
Disadvantages of interleaving[edit]
Use of interleaving techniques increases total delay. This is because the entire interleaved block must be received before the packets can be decoded.[23] Also interleavers hide the structure of errors; without an interleaver, more advanced decoding algorithms can take advantage of the error structure and achieve more reliable communication than a simpler decoder combined with an interleaver[citation needed]. An example of such an algorithm is based on neural network[24] structures.
Software for error-correcting codes[edit]
Simulating the behaviour of error-correcting codes (ECCs) in software is a common practice to design, validate and improve ECCs. The upcoming wireless 5G standard raises a new range of applications for the software ECCs: the Cloud Radio Access Networks (C-RAN) in a Software-defined radio (SDR) context. The idea is to directly use software ECCs in the communications. For instance in the 5G, the software ECCs could be located in the cloud and the antennas connected to this computing resources: improving this way the flexibility of the communication network and eventually increasing the energy efficiency of the system.
In this context, there are various available Open-source software listed below (non exhaustive).
- AFF3CT(A Fast Forward Error Correction Toolbox): a full communication chain in C++ (many supported codes like Turbo, LDPC, Polar codes, etc.), very fast and specialized on channel coding (can be used as a program for simulations or as a library for the SDR).
- IT++: a C++ library of classes and functions for linear algebra, numerical optimization, signal processing, communications, and statistics.
- OpenAir: implementation (in C) of the 3GPP specifications concerning the Evolved Packet Core Networks.
List of error-correcting codes[edit]
| Distance | Code |
|---|---|
| 2 (single-error detecting) | Parity |
| 3 (single-error correcting) | Triple modular redundancy |
| 3 (single-error correcting) | perfect Hamming such as Hamming(7,4) |
| 4 (SECDED) | Extended Hamming |
| 5 (double-error correcting) | |
| 6 (double-error correct-/triple error detect) | Nordstrom-Robinson code |
| 7 (three-error correcting) | perfect binary Golay code |
| 8 (TECFED) | extended binary Golay code |
- AN codes
- Algebraic geometry code
- BCH code, which can be designed to correct any arbitrary number of errors per code block.
- Barker code used for radar, telemetry, ultra sound, Wifi, DSSS mobile phone networks, GPS etc.
- Berger code
- Constant-weight code
- Convolutional code
- Expander codes
- Group codes
- Golay codes, of which the Binary Golay code is of practical interest
- Goppa code, used in the McEliece cryptosystem
- Hadamard code
- Hagelbarger code
- Hamming code
- Latin square based code for non-white noise (prevalent for example in broadband over powerlines)
- Lexicographic code
- Linear Network Coding, a type of erasure correcting code across networks instead of point-to-point links
- Long code
- Low-density parity-check code, also known as Gallager code, as the archetype for sparse graph codes
- LT code, which is a near-optimal rateless erasure correcting code (Fountain code)
- m of n codes
- Nordstrom-Robinson code, used in Geometry and Group Theory[25]
- Online code, a near-optimal rateless erasure correcting code
- Polar code (coding theory)
- Raptor code, a near-optimal rateless erasure correcting code
- Reed–Solomon error correction
- Reed–Muller code
- Repeat-accumulate code
- Repetition codes, such as Triple modular redundancy
- Spinal code, a rateless, nonlinear code based on pseudo-random hash functions[26]
- Tornado code, a near-optimal erasure correcting code, and the precursor to Fountain codes
- Turbo code
- Walsh–Hadamard code
- Cyclic redundancy checks (CRCs) can correct 1-bit errors for messages at most
bits long for optimal generator polynomials of degree
, see Mathematics of cyclic redundancy checks#Bitfilters
See also[edit]
- Code rate
- Erasure codes
- Soft-decision decoder
- Burst error-correcting code
- Error detection and correction
- Error-correcting codes with feedback
- Linear code
- Quantum error correction
References[edit]
- ^ Charles Wang; Dean Sklar; Diana Johnson (Winter 2001–2002). «Forward Error-Correction Coding». Crosslink. The Aerospace Corporation. 3 (1). Archived from the original on 14 March 2012. Retrieved 5 March 2006.
- ^ Charles Wang; Dean Sklar; Diana Johnson (Winter 2001–2002). «Forward Error-Correction Coding». Crosslink. The Aerospace Corporation. 3 (1). Archived from the original on 14 March 2012. Retrieved 5 March 2006.
How Forward Error-Correcting Codes Work]
- ^ a b Maunder, Robert (2016). «Overview of Channel Coding».
- ^ Glover, Neal; Dudley, Trent (1990). Practical Error Correction Design For Engineers (Revision 1.1, 2nd ed.). CO, USA: Cirrus Logic. ISBN 0-927239-00-0.
- ^ a b Hamming, Richard Wesley (April 1950). «Error Detecting and Error Correcting Codes». Bell System Technical Journal. USA: AT&T. 29 (2): 147–160. doi:10.1002/j.1538-7305.1950.tb00463.x. S2CID 61141773.
- ^ «Hamming codes for NAND flash memory devices» Archived 21 August 2016 at the Wayback Machine. EE Times-Asia. Apparently based on «Micron Technical Note TN-29-08: Hamming Codes for NAND Flash Memory Devices». 2005. Both say: «The Hamming algorithm is an industry-accepted method for error detection and correction in many SLC NAND flash-based applications.»
- ^ a b «What Types of ECC Should Be Used on Flash Memory?» (Application note). Spansion. 2011.
Both Reed–Solomon algorithm and BCH algorithm are common ECC choices for MLC NAND flash. … Hamming based block codes are the most commonly used ECC for SLC…. both Reed–Solomon and BCH are able to handle multiple errors and are widely used on MLC flash.
- ^ Jim Cooke (August 2007). «The Inconvenient Truths of NAND Flash Memory» (PDF). p. 28.
For SLC, a code with a correction threshold of 1 is sufficient. t=4 required … for MLC.
- ^ Baldi, M.; Chiaraluce, F. (2008). «A Simple Scheme for Belief Propagation Decoding of BCH and RS Codes in Multimedia Transmissions». International Journal of Digital Multimedia Broadcasting. 2008: 1–12. doi:10.1155/2008/957846.
- ^ Shah, Gaurav; Molina, Andres; Blaze, Matt (2006). «Keyboards and covert channels». USENIX. Retrieved 20 December 2018.
- ^ Tse, David; Viswanath, Pramod (2005), Fundamentals of Wireless Communication, Cambridge University Press, UK
- ^ Shannon, C. E. (1948). «A mathematical theory of communication» (PDF). Bell System Technical Journal. 27 (3–4): 379–423 & 623–656. doi:10.1002/j.1538-7305.1948.tb01338.x. hdl:11858/00-001M-0000-002C-4314-2.
- ^ Rosas, F.; Brante, G.; Souza, R. D.; Oberli, C. (2014). «Optimizing the code rate for achieving energy-efficient wireless communications». Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC). pp. 775–780. doi:10.1109/WCNC.2014.6952166. ISBN 978-1-4799-3083-8.
- ^ IEEE Standard, section 20.3.11.6 «802.11n-2009» Archived 3 February 2013 at the Wayback Machine, IEEE, 29 October 2009, accessed 21 March 2011.
- ^ a b Vucetic, B.; Yuan, J. (2000). Turbo codes: principles and applications. Springer Verlag. ISBN 978-0-7923-7868-6.
- ^ Luby, Michael; Mitzenmacher, M.; Shokrollahi, A.; Spielman, D.; Stemann, V. (1997). «Practical Loss-Resilient Codes». Proc. 29th Annual Association for Computing Machinery (ACM) Symposium on Theory of Computation.
- ^ «Digital Video Broadcast (DVB); Second generation framing structure, channel coding and modulation systems for Broadcasting, Interactive Services, News Gathering and other satellite broadband applications (DVB-S2)». En 302 307. ETSI (V1.2.1). April 2009.
- ^ Andrews, K. S.; Divsalar, D.; Dolinar, S.; Hamkins, J.; Jones, C. R.; Pollara, F. (November 2007). «The Development of Turbo and LDPC Codes for Deep-Space Applications». Proceedings of the IEEE. 95 (11): 2142–2156. doi:10.1109/JPROC.2007.905132. S2CID 9289140.
- ^ Dolinar, S.; Divsalar, D. (15 August 1995). «Weight Distributions for Turbo Codes Using Random and Nonrandom Permutations». TDA Progress Report. 122: 42–122. Bibcode:1995TDAPR.122…56D. CiteSeerX 10.1.1.105.6640.
- ^ Takeshita, Oscar (2006). «Permutation Polynomial Interleavers: An Algebraic-Geometric Perspective». IEEE Transactions on Information Theory. 53 (6): 2116–2132. arXiv:cs/0601048. Bibcode:2006cs……..1048T. doi:10.1109/TIT.2007.896870. S2CID 660.
- ^ 3GPP TS 36.212, version 8.8.0, page 14
- ^ «Digital Video Broadcast (DVB); Frame structure, channel coding and modulation for a second generation digital terrestrial television broadcasting system (DVB-T2)». En 302 755. ETSI (V1.1.1). September 2009.
- ^ Techie (3 June 2010). «Explaining Interleaving». W3 Techie Blog. Retrieved 3 June 2010.
- ^ Krastanov, Stefan; Jiang, Liang (8 September 2017). «Deep Neural Network Probabilistic Decoder for Stabilizer Codes». Scientific Reports. 7 (1): 11003. arXiv:1705.09334. Bibcode:2017NatSR…711003K. doi:10.1038/s41598-017-11266-1. PMC 5591216. PMID 28887480.
- ^ Nordstrom, A.W.; Robinson, J.P. (1967), «An optimum nonlinear code», Information and Control, 11 (5–6): 613–616, doi:10.1016/S0019-9958(67)90835-2
- ^ Perry, Jonathan; Balakrishnan, Hari; Shah, Devavrat (2011). «Rateless Spinal Codes». Proceedings of the 10th ACM Workshop on Hot Topics in Networks. pp. 1–6. doi:10.1145/2070562.2070568. hdl:1721.1/79676. ISBN 9781450310598.
Further reading[edit]
- MacWilliams, Florence Jessiem; Sloane, Neil James Alexander (2007) [1977]. Written at AT&T Shannon Labs, Florham Park, New Jersey, USA. The Theory of Error-Correcting Codes. North-Holland Mathematical Library. Vol. 16 (digital print of 12th impression, 1st ed.). Amsterdam / London / New York / Tokyo: North-Holland / Elsevier BV. ISBN 978-0-444-85193-2. LCCN 76-41296. (xxii+762+6 pages)
- Clark, Jr., George C.; Cain, J. Bibb (1981). Error-Correction Coding for Digital Communications. New York, USA: Plenum Press. ISBN 0-306-40615-2.
- Arazi, Benjamin (1987). Swetman, Herb (ed.). A Commonsense Approach to the Theory of Error Correcting Codes. MIT Press Series in Computer Systems. Vol. 10 (1 ed.). Cambridge, Massachusetts, USA / London, UK: Massachusetts Institute of Technology. ISBN 0-262-01098-4. LCCN 87-21889. (x+2+208+4 pages)
- Wicker, Stephen B. (1995). Error Control Systems for Digital Communication and Storage. Englewood Cliffs, New Jersey, USA: Prentice-Hall. ISBN 0-13-200809-2.
- Wilson, Stephen G. (1996). Digital Modulation and Coding. Englewood Cliffs, New Jersey, USA: Prentice-Hall. ISBN 0-13-210071-1.
- «Error Correction Code in Single Level Cell NAND Flash memories» 2007-02-16
- «Error Correction Code in NAND Flash memories» 2004-11-29
- Observations on Errors, Corrections, & Trust of Dependent Systems, by James Hamilton, 2012-02-26
- Sphere Packings, Lattices and Groups, By J. H. Conway, Neil James Alexander Sloane, Springer Science & Business Media, 2013-03-09 – Mathematics – 682 pages.
External links[edit]
- Morelos-Zaragoza, Robert (2004). «The Correcting Codes (ECC) Page». Retrieved 5 March 2006.
- lpdec: library for LP decoding and related things (Python)
Современный жёсткий диск — уникальный компонент компьютера. Он уникален тем, что хранит в себе служебную информацию, изучая которую, можно оценить «здоровье» диска. Эта информация содержит в себе историю изменения множества параметров, отслеживаемых винчестером в процессе функционирования. Больше ни один компонент системного блока не предоставляет владельцу статистику своей работы! Вкупе с тем, что HDD является одним из самых ненадёжных компонентов компьютера, такая статистика может быть весьма полезной и помочь его владельцу избежать нервотрёпки и потери денег и времени.
Информация о состоянии диска доступна благодаря комплексу технологий, называемых общим именем S.M.A.R.T. (Self-Monitoring, Analisys and Reporting Technology, т. е. технология самомониторинга, анализа и отчёта). Этот комплекс довольно обширен, но мы поговорим о тех его аспектах, которые позволяют посмотреть на атрибуты S.M.A.R.T., отображаемые в какой-либо программе по тестированию винчестера, и понять, что творится с диском.
Отмечу, что нижесказанное относится к дискам с интерфейсами SATA и РАТА. У дисков SAS, SCSI и других серверных дисков тоже есть S.M.A.R.T., но его представление сильно отличается от SATA/PATA. Да и мониторит серверные диски обычно не человек, а RAID-контроллер, потому про них мы говорить не будем.
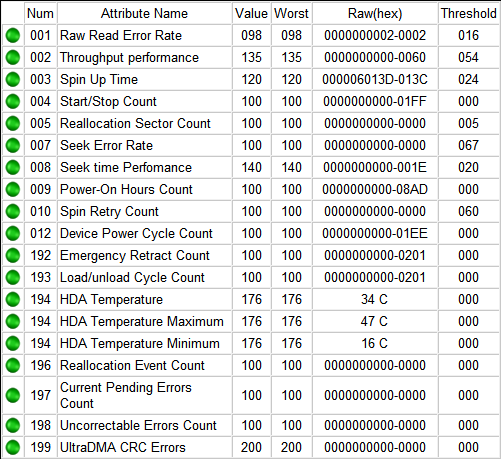
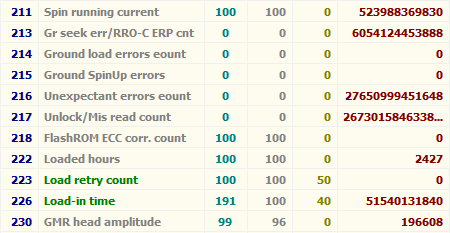
Итак, если мы откроем S.M.A.R.T. в какой-либо из многочисленных программ, то увидим приблизительно следующую картину (на скриншоте приведён S.M.A.R.T. диска Hitachi Deskstar 7К1000.С HDS721010CLA332 в HDDScan 3.3):
S.M.A.R.T. в HDDScan 3.3
В каждой строке отображается отдельный атрибут S.M.A.R.T. Атрибуты имеют более-менее стандартизованные названия и определённый номер, которые не зависят от модели и производителя диска.
Каждый атрибут S.M.A.R.T. имеет несколько полей. Каждое поле относится к определённому классу из следующих: ID, Value, Worst, Threshold и RAW. Рассмотрим каждый из классов.
- ID (может также именоваться Number) — идентификатор, номер атрибута в технологии S.M.A.R.T. Название одного и того же атрибута программами может выдаваться по-разному, а вот идентификатор всегда однозначно определяет атрибут. Особенно это полезно в случае программ, которые переводят общепринятое название атрибута с английского языка на русский. Иногда получается такая белиберда, что понять, что же это за параметр, можно только по его идентификатору.
- Value (Current) — текущее значение атрибута в попугаях (т. е. в величинах неизвестной размерности). В процессе работы винчестера оно может уменьшаться, увеличиваться и оставаться неизменным. По показателю Value нельзя судить о «здоровье» атрибута, не сравнивая его со значением Threshold этого же атрибута. Как правило, чем меньше Value, тем хуже состояние атрибута (изначально все классы значений, кроме RAW, на новом диске имеют максимальное из возможных значение, например 100).
- Worst — наихудшее значение, которого достигало значение Value за всю жизнь винчестера. Измеряется тоже в «попугаях». В процессе работы оно может уменьшаться либо оставаться неизменным. По нему тоже нельзя однозначно судить о здоровье атрибута, нужно сравнивать его с Threshold.
- Threshold — значение в «попугаях», которого должен достигнуть Value этого же атрибута, чтобы состояние атрибута было признано критическим. Проще говоря, Threshold — это порог: если Value больше Threshold — атрибут в порядке; если меньше либо равен — с атрибутом проблемы. Именно по такому критерию утилиты, читающие S.M.A.R.T., выдают отчёт о состоянии диска либо отдельного атрибута вроде «Good» или «Bad». При этом они не учитывают, что даже при Value, большем Threshold, диск на самом деле уже может быть умирающим с точки зрения пользователя, а то и вовсе ходячим мертвецом, поэтому при оценке здоровья диска смотреть стоит всё-таки на другой класс атрибута, а именно — RAW. Однако именно значение Value, опустившееся ниже Threshold, может стать легитимным поводом для замены диска по гарантии (для самих гарантийщиков, конечно же) — кто же яснее скажет о здоровье диска, как не он сам, демонстрируя текущее значение атрибута хуже критического порога? Т. е. при значении Value, большем Threshold, сам диск считает, что атрибут здоров, а при меньшем либо равном — что болен. Очевидно, что при Threshold=0 состояние атрибута не будет признано критическим никогда. Threshold — постоянный параметр, зашитый производителем в диске.
- RAW (Data) — самый интересный, важный и нужный для оценки показатель. В большинстве случаев он содержит в себе не «попугаи», а реальные значения, выражаемые в различных единицах измерения, напрямую говорящие о текущем состоянии диска. Основываясь именно на этом показателе, формируется значение Value (а вот по какому алгоритму оно формируется — это уже тайна производителя, покрытая мраком). Именно умение читать и анализировать поле RAW даёт возможность объективно оценить состояние винчестера.
Этим мы сейчас и займёмся — разберём все наиболее используемые атрибуты S.M.A.R.T., посмотрим, о чём они говорят и что нужно делать, если они не в порядке.
| Аттрибуты S.M.A.R.T. | |||||||||||||||||
| 01 | 02 | 03 | 04 | 05 | 07 | 08 | 09 | 10 | 11 | 12 | 183 | 184 | 187 | 188 | 189 | 190 | |
| 0x | 01 | 02 | 03 | 04 | 05 | 07 | 08 | 09 | 0A | 0B | 0C | B7 | B8 | BB | BC | BD | BE |
| 191 | 192 | 193 | 194 | 195 | 196 | 197 | 198 | 199 | 200 | 201 | 202 | 203 | 220 | 240 | 254 | ||
| 0x | BF | С0 | С1 | С2 | С3 | С4 | С5 | С6 | С7 | С8 | С9 | СА | CB | DC | F0 | FE |
Перед тем как описывать атрибуты и допустимые значения их поля RAW, уточню, что атрибуты могут иметь поле RAW разного типа: текущее и накапливающее. Текущее поле содержит значение атрибута в настоящий момент, для него свойственно периодическое изменение (для одних атрибутов — изредка, для других — много раз за секунду; другое дело, что в программах чтения S.M.A.R.T. такое быстрое изменение не отображается). Накапливающее поле — содержит статистику, обычно в нём содержится количество возникновений конкретного события со времени первого запуска диска.
Текущий тип характерен для атрибутов, для которых нет смысла суммировать их предыдущие показания. Например, показатель температуры диска является текущим: его цель — в демонстрации температуры в настоящий момент, а не суммы всех предыдущих температур. Накапливающий тип свойственен атрибутам, для которых весь их смысл заключается в предоставлении информации за весь период «жизни» винчестера. Например, атрибут, характеризующий время работы диска, является накапливающим, т. е. содержит количество единиц времени, отработанных накопителем за всю его историю.
Приступим к рассмотрению атрибутов и их RAW-полей.
Атрибут: 01 Raw Read Error Rate
| Тип | текущий, может быть накапливающим для WD и старых Hitachi |
| Описание | содержит частоту возникновения ошибок при чтении с пластин |
Для всех дисков Seagate, Samsung (начиная с семейства SpinPoint F1 (включительно)) и Fujitsu 2,5″ характерны огромные числа в этих полях.
Для остальных дисков Samsung и всех дисков WD в этом поле характерен 0.
Для дисков Hitachi в этом поле характерен 0 либо периодическое изменение поля в пределах от 0 до нескольких единиц.
Такие отличия обусловлены тем, что все жёсткие диски Seagate, некоторые Samsung и Fujitsu считают значения этих параметров не так, как WD, Hitachi и другие Samsung. При работе любого винчестера всегда возникают ошибки такого рода, и он преодолевает их самостоятельно, это нормально, просто на дисках, которые в этом поле содержат 0 или небольшое число, производитель не счёл нужным указывать истинное количество этих ошибок.
Таким образом, ненулевой параметр на дисках WD и Samsung до SpinPoint F1 (не включительно) и большое значение параметра на дисках Hitachi могут указывать на аппаратные проблемы с диском. Необходимо учитывать, что утилиты могут отображать несколько значений, содержащихся в поле RAW этого атрибута, как одно, и оно будет выглядеть весьма большим, хоть это и будет неверно (подробности см. ниже).
На дисках Seagate, Samsung (SpinPoint F1 и новее) и Fujitsu на этот атрибут можно не обращать внимания.
Атрибут: 02 Throughput Performance
| Тип | текущий |
| Описание | содержит значение средней производительности диска и измеряется в каких-то «попугаях». Обычно его ненулевое значение отмечается на винчестерах Hitachi. На них он может изменяться после изменения параметров ААМ, а может и сам по себе по неизвестному алгоритму |
Параметр не даёт никакой информации пользователю и не говорит ни о какой опасности при любом своём значении.
Атрибут: 03 Spin-Up Time
| Тип | текущий |
| Описание | содержит время, за которое шпиндель диска в последний раз разогнался из состояния покоя до номинальной скорости. Может содержать два значения — последнее и, например, минимальное время раскрутки. Может измеряться в миллисекундах, десятках миллисекунд и т. п. — это зависит от производителя и модели диска |
Время разгона может различаться у разных дисков (причём у дисков одного производителя тоже) в зависимости от тока раскрутки, массы блинов, номинальной скорости шпинделя и т. п.
Кстати, винчестеры Fujitsu всегда имеют единицу в этом поле в случае отсутствия проблем с раскруткой шпинделя.
Практически ничего не говорит о здоровье диска, поэтому при оценке состояния винчестера на параметр можно не обращать внимания.
Атрибут: 04 Number of Spin-Up Times (Start/Stop Count)
| Тип | накапливающий |
| Описание | содержит количество раз включения диска. Бывает ненулевым на только что купленном диске, находившемся в запаянной упаковке, что может говорить о тестировании диска на заводе. Или ещё о чём-то, мне не известном  |
При оценке здоровья не обращайте на атрибут внимания.
Атрибут: 05 Reallocated Sector Count
| Тип | накапливающий |
| Описание | содержит количество секторов, переназначенных винчестером в резервную область. Практически ключевой параметр в оценке состояния |
Поясним, что вообще такое «переназначенный сектор». Когда диск в процессе работы натыкается на нечитаемый/плохо читаемый/незаписываемый/плохо записываемый сектор, он может посчитать его невосполнимо повреждённым. Специально для таких случаев производитель предусматривает на каждом диске (на каких-то моделях — в центре (логическом конце) диска, на каких-то — в конце каждого трека и т. д.) резервную область. При наличии повреждённого сектора диск помечает его как нечитаемый и использует вместо него сектор в резервной области, сделав соответствующие пометки в специальном списке дефектов поверхности — G-list. Такая операция по назначению нового сектора на роль старого называется remap (ремап) либо переназначение, а используемый вместо повреждённого сектор — переназначенным. Новый сектор получает логический номер LBA старого, и теперь при обращении ПО к сектору с этим номером (программы же не знают ни о каких переназначениях!) запрос будет перенаправляться в резервную область.
Таким образом, хоть сектор и вышел из строя, объём диска не изменяется. Понятно, что не изменяется он до поры до времени, т. к. объём резервной области не бесконечен. Однако резервная область вполне может содержать несколько тысяч секторов, и допустить, чтобы она закончилась, будет весьма безответственно — диск нужно будет заменить задолго до этого.
Кстати, ремонтники говорят, что диски Samsung очень часто ни в какую не хотят выполнять переназначение секторов.
На счёт этого атрибута мнения разнятся. Лично я считаю, что если он достиг 10, диск нужно обязательно менять — ведь это означает прогрессирующий процесс деградации состояния поверхности либо блинов, либо головок, либо чего-то ещё аппаратного, и остановить этот процесс возможности уже нет. Кстати, по сведениям лиц, приближенных к Hitachi, сама Hitachi считает диск подлежащим замене, когда на нём находится уже 5 переназначенных секторов. Другой вопрос, официальная ли эта информация, и следуют ли этому мнению сервис-центры. Что-то мне подсказывает, что нет 
Другое дело, что сотрудники сервис-центров могут отказываться признавать диск неисправным, если фирменная утилита производителя диска пишет что-то вроде «S.M.A.R.T. Status: Good» или значения Value либо Worst атрибута будут больше Threshold (собственно, по такому критерию может оценивать и сама утилита производителя). И формально они будут правы. Но кому нужен диск с постоянным ухудшением его аппаратных компонентов, даже если такое ухудшение соответствует природе винчестера, а технология производства жёстких дисков старается минимизировать его последствия, выделяя, например, резервную область?
Атрибут: 07 Seek Error Rate
| Тип | текущий |
| Описание | содержит частоту возникновения ошибок при позиционировании блока магнитных головок (БМГ) |
Описание формирования этого атрибута почти полностью совпадает с описанием для атрибута 01 Raw Read Error Rate, за исключением того, что для винчестеров Hitachi нормальным значением поля RAW является только 0.
Таким образом, на атрибут на дисках Seagate, Samsung SpinPoint F1 и новее и Fujitsu 2,5″ не обращайте внимания, на остальных моделях Samsung, а также на всех WD и Hitachi ненулевое значение свидетельствует о проблемах, например, с подшипником и т. п.
Атрибут: 08 Seek Time Performance
| Тип | текущий |
| Описание | содержит среднюю производительность операций позиционирования головок, измеряется в «попугаях». Как и параметр 02 Throughput Performance, ненулевое значение обычно отмечается на дисках Hitachi и может изменяться после изменения параметров ААМ, а может и само по себе по неизвестному алгоритму |
Не даёт никакой информации пользователю и не говорит ни о какой опасности при любом своём значении.
Атрибут: 09 Power On Hours Count (Power-on Time)
| Тип | накапливающий |
| Описание | содержит количество часов, в течение которых винчестер был включён |
Ничего не говорит о здоровье диска.
Атрибут: 10 (0А — в шестнадцатеричной системе счисления) Spin Retry Count
| Тип | накапливающий |
| Описание | содержит количество повторов запуска шпинделя, если первая попытка оказалась неудачной |
О здоровье диска чаще всего не говорит.
Основные причины увеличения параметра — плохой контакт диска с БП или невозможность БП выдать нужный ток в линию питания диска.
В идеале должен быть равен 0. При значении атрибута, равном 1-2, внимания можно не обращать. Если значение больше, в первую очередь следует обратить пристальное внимание на состояние блока питания, его качество, нагрузку на него, проверить контакт винчестера с кабелем питания, проверить сам кабель питания.
Наверняка диск может стартовать не сразу из-за проблем с ним самим, но такое бывает очень редко, и такую возможность нужно рассматривать в последнюю очередь.
Атрибут: 11 (0B) Calibration Retry Count (Recalibration Retries)
| Тип | накапливающий |
| Описание | содержит количество повторных попыток сброса накопителя (установки БМГ на нулевую дорожку) при неудачной первой попытке |
Ненулевое, а особенно растущее значение параметра может означать проблемы с диском.
Атрибут: 12 (0C) Power Cycle Count
| Тип | накапливающий |
| Описание | содержит количество полных циклов «включение-отключение» диска |
Не связан с состоянием диска.
Атрибут: 183 (B7) SATA Downshift Error Count
| Тип | накапливающий |
| Описание | содержит количество неудачных попыток понижения режима SATA. Суть в том, что винчестер, работающий в режимах SATA 3 Гбит/с или 6 Гбит/с (и что там дальше будет в будущем), по какой-то причине (например, из-за ошибок) может попытаться «договориться» с дисковым контроллером о менее скоростном режиме (например, SATA 1,5 Гбит/с или 3 Гбит/с соответственно). В случае «отказа» контроллера изменять режим диск увеличивает значение атрибута |
Не говорит о здоровье накопителя.
Атрибут: 184 (B8) End-to-End Error
| Тип | накапливающий |
| Описание | содержит количество ошибок, возникших при передаче данных через кэш винчестера |
Ненулевое значение указывает на проблемы с диском.
Атрибут: 187 (BB) Reported Uncorrected Sector Count (UNC Error)
| Тип | накапливающий |
| Описание | содержит количество секторов, которые были признаны кандидатами на переназначение (см. атрибут 197) за всю историю жизни диска. Причём если сектор становится кандидатом повторно, значение атрибута тоже увеличивается |
Ненулевое значение атрибута явно указывает на ненормальное состояние диска (в сочетании с ненулевым значением атрибута 197) или на то, что оно было таковым ранее (в сочетании с нулевым значением 197).
Атрибут: 188 (BC) Command Timeout
| Тип | накапливающий |
| Описание | содержит количество операций, выполнение которых было отменено из-за превышения максимально допустимого времени ожидания отклика |
Такие ошибки могут возникать из-за плохого качества кабелей, контактов, используемых переходников, удлинителей и т. д., а также из-за несовместимости диска с конкретным контроллером SATA/РАТА на материнской плате (либо дискретным). Из-за ошибок такого рода возможны BSOD в Windows.
Ненулевое значение атрибута говорит о потенциальной «болезни» диска.
Атрибут: 189 (BD) High Fly Writes
| Тип | накапливающий |
| Описание | содержит количество зафиксированных случаев записи при высоте полета головки выше рассчитанной — скорее всего, из-за внешних воздействий, например вибрации |
Для того чтобы сказать, почему происходят такие случаи, нужно уметь анализировать логи S.M.A.R.T., которые содержат специфичную для каждого производителя информацию, что на сегодняшний день не реализовано в общедоступном ПО — следовательно, на атрибут можно не обращать внимания.
Атрибут: 190 (BE) Airflow Temperature
| Тип | текущий |
| Описание | содержит температуру винчестера для дисков Hitachi, Samsung, WD и значение «100 − [RAW-значение атрибута 194]» для Seagate |
Не говорит о состоянии диска.
Атрибут: 191 (BF) G-Sensor Shock Count (Mechanical Shock)
| Тип | накапливающий |
| Описание | содержит количество критических ускорений, зафиксированных электроникой диска, которым подвергался накопитель и которые превышали допустимые. Обычно это происходит при ударах, падениях и т. п. |
Актуален для мобильных винчестеров. На дисках Samsung на него часто можно не обращать внимания, т. к. они могут иметь очень чувствительный датчик, который, образно говоря, реагирует чуть ли не на движение воздуха от крыльев пролетающей в одном помещении с диском мухи.
Вообще срабатывание датчика не является признаком удара. Может расти даже от позиционирования БМГ самим диском, особенно если его не закрепить. Основное назначение датчика — прекратить операцию записи при вибрациях, чтобы избежать ошибок.
Не говорит о здоровье диска.
Атрибут: 192 (С0) Power Off Retract Count (Emergency Retry Count)
| Тип | накапливающий |
| Описание | для разных винчестеров может содержать одну из следующих двух характеристик: либо суммарное количество парковок БМГ диска в аварийных ситуациях (по сигналу от вибродатчика, обрыву/понижению питания и т. п.), либо суммарное количество циклов включения/выключения питания диска (характерно для современных WD и Hitachi) |
Не позволяет судить о состоянии диска.
Атрибут: 193 (С1) Load/Unload Cycle Count
| Тип | накапливающий |
| Описание | содержит количество полных циклов парковки/распарковки БМГ. Анализ этого атрибута — один из способов определить, включена ли на диске функция автоматической парковки (столь любимая, например, компанией Western Digital): если его содержимое превосходит (обычно — многократно) содержимое атрибута 09 — счётчик отработанных часов, — то парковка включена |
Не говорит о здоровье диска.
Атрибут: 194 (С2) Temperature (HDA Temperature, HDD Temperature)
| Тип | текущий/накапливающий |
| Описание | содержит текущую температуру диска. Температура считывается с датчика, который на разных моделях может располагаться в разных местах. Поле вместе с текущей также может содержать максимальную и минимальную температуры, зафиксированные за всё время эксплуатации винчестера |
О состоянии диска атрибут не говорит, но позволяет контролировать один из важнейших параметров. Моё мнение: при работе старайтесь не допускать повышения температуры винчестера выше 50 градусов, хоть производителем обычно и декларируется максимальный предел температуры в 55-60 градусов.
Атрибут: 195 (С3) Hardware ECC Recovered
| Тип | накапливающий |
| Описание | содержит количество ошибок, которые были скорректированы аппаратными средствами ECC диска |
Особенности, присущие этому атрибуту на разных дисках, полностью соответствуют таковым атрибутов 01 и 07.
Атрибут: 196 (С4) Reallocated Event Count
| Тип | накапливающий |
| Описание | содержит количество операций переназначения секторов |
Косвенно говорит о здоровье диска. Чем больше значение — тем хуже. Однако нельзя однозначно судить о здоровье диска по этому параметру, не рассматривая другие атрибуты.
Этот атрибут непосредственно связан с атрибутом 05. При росте 196 чаще всего растёт и 05. Если при росте атрибута 196 атрибут 05 не растёт, значит, при попытке ремапа кандидат в бэд-блоки оказался софт-бэдом (подробности см. ниже), и диск исправил его, так что сектор был признан здоровым, и в переназначении не было необходимости.
Если атрибут 196 меньше атрибута 05, значит, во время некоторых операций переназначения выполнялся перенос нескольких повреждённых секторов за один приём.
Если атрибут 196 больше атрибута 05, значит, при некоторых операциях переназначения были обнаружены исправленные впоследствии софт-бэды.
Атрибут: 197 (С5) Current Pending Sector Count
| Тип | текущий |
| Описание | содержит количество секторов-кандидатов на переназначение в резервную область |
Натыкаясь в процессе работы на «нехороший» сектор (например, контрольная сумма сектора не соответствует данным в нём), диск помечает его как кандидат на переназначение, заносит его в специальный внутренний список и увеличивает параметр 197. Из этого следует, что на диске могут быть повреждённые секторы, о которых он ещё не знает — ведь на пластинах вполне могут быть области, которые винчестер какое-то время не использует.
При попытке записи в сектор диск сначала проверяет, не находится ли этот сектор в списке кандидатов. Если сектор там не найден, запись проходит обычным порядком. Если же найден, проводится тестирование этого сектора записью-чтением. Если все тестовые операции проходят нормально, то диск считает, что сектор исправен. (Т. е. был т. н. «софт-бэд» — ошибочный сектор возник не по вине диска, а по иным причинам: например, в момент записи информации отключилось электричество, и диск прервал запись, запарковав БМГ. В итоге данные в секторе окажутся недописанными, а контрольная сумма сектора, зависящая от данных в нём, вообще останется старой. Налицо будет расхождение между нею и данными в секторе.) В таком случае диск проводит изначально запрошенную запись и удаляет сектор из списка кандидатов. При этом атрибут 197 уменьшается, также возможно увеличение атрибута 196.
Если же тестирование заканчивается неудачей, диск выполняет операцию переназначения, уменьшая атрибут 197, увеличивая 196 и 05, а также делает пометки в G-list.
Итак, ненулевое значение параметра говорит о неполадках (правда, не может сказать о том, в само́м ли диске проблема).
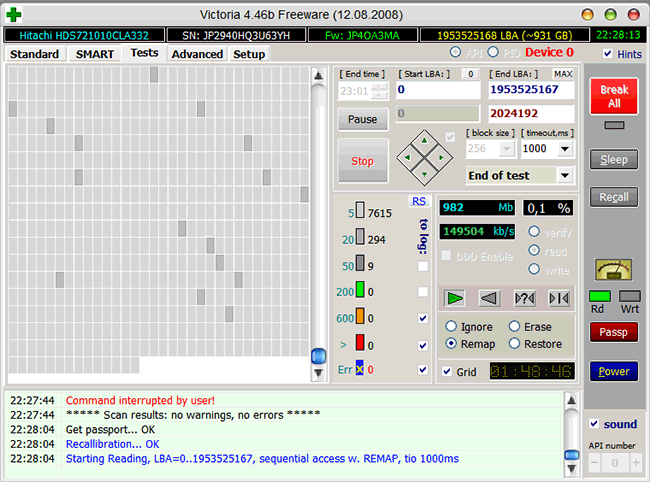
При ненулевом значении нужно обязательно запустить в программах Victoria или MHDD последовательное чтение всей поверхности с опцией remap. Тогда при сканировании диск обязательно наткнётся на плохой сектор и попытается произвести запись в него (в случае Victoria 3.5 и опции Advanced remap — диск будет пытаться записать сектор до 10 раз). Таким образом программа спровоцирует «лечение» сектора, и в итоге сектор будет либо исправлен, либо переназначен.
Идёт последовательное чтение с ремапом в Victoria 4.46b
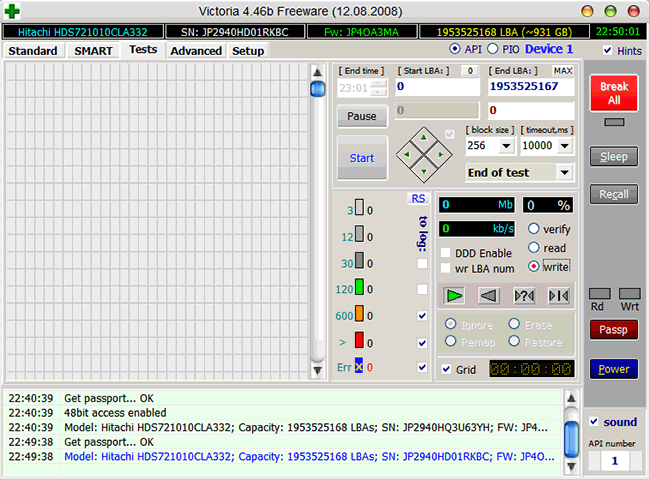
В случае неудачи чтения как с remap, так и с Advanced remap, стоит попробовать запустить последовательную запись в тех же Victoria или MHDD. Учитывайте, что операция записи стирает данные, поэтому перед её применением обязательно делайте бэкап!
Запуск последовательной записи в Victoria 4.46b
Иногда от невыполнения ремапа могут помочь следующие манипуляции: снимите плату электроники диска и почистите контакты гермоблока винчестера, соединяющие его с платой — они могут быть окислены. Будь аккуратны при выполнении этой процедуры — из-за неё можно лишиться гарантии!
Невозможность ремапа может быть обусловлена ещё одной причиной — диск исчерпал резервную область, и ему просто некуда переназначать секторы.
Если же значение атрибута 197 никакими манипуляциями не снижается до 0, следует думать о замене диска.
Атрибут: 198 (С6) Offline Uncorrectable Sector Count (Uncorrectable Sector Count)
| Тип | текущий |
| Описание | означает то же самое, что и атрибут 197, но отличие в том, что данный атрибут содержит количество секторов-кандидатов, обнаруженных при одном из видов самотестирования диска — оффлайн-тестировании, которое диск запускает в простое в соответствии с параметрами, заданными прошивкой |
Параметр этот изменяется только под воздействием оффлайн-тестирования, никакие сканирования программами на него не влияют. При операциях во время самотестирования поведение атрибута такое же, как и атрибута 197.
Ненулевое значение говорит о неполадках на диске (точно так же, как и 197, не конкретизируя, кто виноват).
Атрибут: 199 (С7) UltraDMA CRC Error Count
| Тип | накапливающий |
| Описание | содержит количество ошибок, возникших при передаче по интерфейсному кабелю в режиме UltraDMA (или его эмуляции винчестерами SATA) от материнской платы или дискретного контроллера контроллеру диска |
В подавляющем большинстве случаев причинами ошибок становятся некачественный шлейф передачи данных, разгон шин PCI/PCI-E компьютера либо плохой контакт в SATA-разъёме на диске или на материнской плате/контроллере.
Ошибки при передаче по интерфейсу и, как следствие, растущее значение атрибута могут приводить к переключению операционной системой режима работы канала, на котором находится накопитель, в режим PIO, что влечёт резкое падение скорости чтения/записи при работе с ним и загрузку процессора до 100% (видно в Диспетчере задач Windows).
В случае винчестеров Hitachi серий Deskstar 7К3000 и 5К3000 растущий атрибут может говорить о несовместимости диска и SATA-контроллера. Чтобы исправить ситуацию, нужно принудительно переключить такой диск в режим SATA 3 Гбит/с.
Моё мнение: при наличии ошибок — переподключите кабель с обоих концов; если их количество растёт и оно больше 10 — выбрасывайте шлейф и ставьте вместо него новый или снимайте разгон.
Можно считать, что о здоровье диска атрибут не говорит.
Атрибут: 200 (С8) Write Error Rate (MultiZone Error Rate)
| Тип | текущий |
| Описание | содержит частоту возникновения ошибок при записи |
Ненулевое значение говорит о проблемах с диском — в частности, у дисков WD большие цифры могут означать «умирающие» головки.
Атрибут: 201 (С9) Soft Read Error Rate
| Тип | текущий |
| Описание | содержит частоту возникновения ошибок чтения, произошедших по вине программного обеспечения |
Влияние на здоровье неизвестно.
Атрибут: 202 (СА) Data Address Mark Error
| Тип | неизвестно |
| Описание | содержание атрибута — загадка, но проанализировав различные диски, могу констатировать, что ненулевое значение — это плохо |
Атрибут: 203 (CB) Run Out Cancel
| Тип | текущий |
| Описание | содержит количество ошибок ECC |
Влияние на здоровье неизвестно.
Атрибут: 220 (DC) Disk Shift
| Тип | текущий |
| Описание | содержит измеренный в неизвестных единицах сдвиг пластин диска относительно оси шпинделя |
Влияние на здоровье неизвестно.
Атрибут: 240 (F0) Head Flying Hours
| Тип | накапливающий |
| Описание | содержит время, затраченное на позиционирование БМГ. Счётчик может содержать несколько значений в одном поле |
Влияние на здоровье неизвестно.
Атрибут: 254 (FE) Free Fall Event Count
| Тип | накапливающий |
| Описание | содержит зафиксированное электроникой количество ускорений свободного падения диска, которым он подвергался, т. е., проще говоря, показывает, сколько раз диск падал |
Влияние на здоровье неизвестно.
Подытожим описание атрибутов. Ненулевые значения:
- атрибутов 01, 07, 195 — вызывают подозрения в «болезни» у некоторых моделей дисков;
- атрибутов 10, 11, 188, 196, 199, 202 — вызывают подозрения у всех дисков;
- и, наконец, атрибутов 05, 184, 187, 197, 198, 200 — прямо говорят о неполадках.
При анализе атрибутов учитывайте, что в некоторых параметрах S.M.A.R.T. могут храниться несколько значений этого параметра: например, для предпоследнего запуска диска и для последнего. Такие параметры длиной в несколько байт логически состоят из нескольких значений длиной в меньшее количество байт — например, параметр, хранящий два значения для двух последних запусков, под каждый из которых отводится 2 байта, будет иметь длину 4 байта. Программы, интерпретирующие S.M.A.R.T., часто не знают об этом, и показывают этот параметр как одно число, а не два, что иногда приводит к путанице и волнению владельца диска. Например, «Raw Read Error Rate», хранящий предпоследнее значение «1» и последнее значение «0», будет выглядеть как 65536.
Надо отметить, что не все программы умеют правильно отображать такие атрибуты. Многие как раз и переводят атрибут с несколькими значениями в десятичную систему счисления как одно огромное число. Правильно же отображать такое содержимое — либо с разбиением по значениям (тогда атрибут будет состоять из нескольких отдельных чисел), либо в шестнадцатеричной системе счисления (тогда атрибут будет выглядеть как одно число, но его составляющие будут легко различимы с первого взгляда), либо и то, и другое одновременно. Примерами правильных программ служат HDDScan, CrystalDiskInfo, Hard Disk Sentinel.
Продемонстрируем отличия на практике. Вот так выглядит мгновенное значение атрибута 01 на одном из моих Hitachi HDS721010CLA332 в неучитывающей особенности этого атрибута Victoria 4.46b:
Атрибут 01 в Victoria 4.46b
А так выглядит он же в «правильной» HDDScan 3.3:
Атрибут 01 в HDDScan 3.3
Плюсы HDDScan в данном контексте очевидны, не правда ли?
Если анализировать S.M.A.R.T. на разных дисках, то можно заметить, что одни и те же атрибуты могут вести себя по-разному. Например, некоторые параметры S.M.A.R.T. винчестеров Hitachi после определённого периода неактивности диска обнуляются; параметр 01 имеет особенности на дисках Hitachi, Seagate, Samsung и Fujitsu, 03 — на Fujitsu. Также известно, что после перепрошивки диска некоторые параметры могут установиться в 0 (например, 199). Однако подобное принудительное обнуление атрибута ни в коем случае не будет говорить о том, что проблемы с диском решены (если таковые были). Ведь растущий критичный атрибут — это следствие неполадок, а не причина.
При анализе множества массивов данных S.M.A.R.T. становится очевидным, что набор атрибутов у дисков разных производителей и даже у разных моделей одного производителя может отличаться. Связано это с так называемыми специфичными для конкретного вендора (vendor specific) атрибутами (т. е. атрибутами, используемыми для мониторинга своих дисков определённым производителем) и не должно являться поводом для волнения. Если ПО мониторинга умеет читать такие атрибуты (например, Victoria 4.46b), то на дисках, для которых они не предназначены, они могут иметь «страшные» (огромные) значения, и на них просто не нужно обращать внимания. Вот так, например, Victoria 4.46b отображает RAW-значения атрибутов, не предназначенных для мониторинга у Hitachi HDS721010CLA332:
«Страшные» значения в Victoria 4.46b
Нередко встречается проблема, когда программы не могут считать S.M.A.R.T. диска. В случае исправного винчестера это может быть вызвано несколькими факторами. Например, очень часто не отображается S.M.A.R.T. при подключении диска в режиме AHCI. В таких случаях стоит попробовать разные программы, в частности HDD Scan, которая обладает умением работать в таком режиме, хоть у неё и не всегда это получается, либо же стоит временно переключить диск в режим совместимости с IDE, если есть такая возможность. Далее, на многих материнских платах контроллеры, к которым подключаются винчестеры, бывают не встроенными в чипсет или южный мост, а реализованы отдельными микросхемами. В таком случае DOS-версия Victoria, например, не увидит подключённый к контроллеру жёсткий диск, и ей нужно будет принудительно указывать его, нажав клавишу [Р] и введя номер канала с диском. Часто не читаются S.M.A.R.T. у USB-дисков, что объясняется тем, что USB-контроллер просто не пропускает команды для чтения S.M.A.R.T. Практически никогда не читается S.M.A.R.T. у дисков, функционирующих в составе RAID-массива. Здесь тоже есть смысл попробовать разные программы, но в случае аппаратных RAID-контроллеров это бесполезно.
Если после покупки и установки нового винчестера какие-либо программы (HDD Life, Hard Drive Inspector и иже с ними) показывают, что: диску осталось жить 2 часа; его производительность — 27%; здоровье — 19,155% (выберите по вкусу) — то паниковать не стоит. Поймите следующее. Во-первых, нужно смотреть на показатели S.M.A.R.T., а не на непонятно откуда взявшиеся числа здоровья и производительности (впрочем, принцип их подсчёта понятен: берётся наихудший показатель). Во-вторых, любая программа при оценке параметров S.M.A.R.T. смотрит на отклонение значений разных атрибутов от предыдущих показаний. При первых запусках нового диска параметры непостоянны, необходимо некоторое время на их стабилизацию. Программа, оценивающая S.M.A.R.T., видит, что атрибуты изменяются, производит расчёты, у неё получается, что при их изменении такими темпами накопитель скоро выйдет из строя, и она начинает сигнализировать: «Спасайте данные!» Пройдёт некоторое время (до пары месяцев), атрибуты стабилизируются (если с диском действительно всё в порядке), утилита наберёт данных для статистики, и сроки кончины диска по мере стабилизации S.M.A.R.T. будут переноситься всё дальше и дальше в будущее. Оценка программами дисков Seagate и Samsung — вообще отдельный разговор. Из-за особенностей атрибутов 1, 7, 195 программы даже для абсолютно здорового диска обычно выдают заключение, что он завернулся в простыню и ползёт на кладбище.
Обратите внимание, что возможна следующая ситуация: все атрибуты S.M.A.R.T. — в норме, однако на самом деле диск — с проблемами, хоть этого пока ни по чему не заметно. Объясняется это тем, что технология S.M.A.R.T. работает только «по факту», т. е. атрибуты меняются только тогда, когда диск в процессе работы встречает проблемные места. А пока он на них не наткнулся, то и не знает о них и, следовательно, в S.M.A.R.T. ему фиксировать нечего.
Таким образом, S.M.A.R.T. — это полезная технология, но пользоваться ею нужно с умом. Кроме того, даже если S.M.A.R.T. вашего диска идеален, и вы постоянно устраиваете диску проверки — не полагайтесь на то, что ваш диск будет «жить» ещё долгие годы. Винчестерам свойственно ломаться так быстро, что S.M.A.R.T. просто не успевает отобразить его изменившееся состояние, а бывает и так, что с диском — явные нелады, но в S.M.A.R.T. — всё в порядке. Можно сказать, что хороший S.M.A.R.T. не гарантирует, что с накопителем всё хорошо, но плохой S.M.A.R.T. гарантированно свидетельствует о проблемах. При этом даже с плохим S.M.A.R.T. утилиты могут показывать, что состояние диска — «здоров», из-за того, что критичными атрибутами не достигнуты пороговые значения. Поэтому очень важно анализировать S.M.A.R.T. самому, не полагаясь на «словесную» оценку программ.
Хоть технология S.M.A.R.T. и работает, винчестеры и понятие «надёжность» настолько несовместимы, что принято считать их просто расходным материалом. Ну, как картриджи в принтере. Поэтому во избежание потери ценных данных делайте их периодическое резервное копирование на другой носитель (например, другой винчестер). Оптимально делать две резервные копии на двух разных носителях, не считая винчестера с оригинальными данными. Да, это ведёт к дополнительным затратам, но поверьте: затраты на восстановление информации со сломавшегося HDD обойдутся вам в разы — если не на порядок-другой — дороже. А ведь данные далеко не всегда могут восстановить даже профессионалы. Т. е. единственная возможность обеспечить надёжное хранение ваших данных — это делать их бэкап.
Напоследок упомяну некоторые программы, которые хорошо подходят для анализа S.M.A.R.T. и тестирования винчестеров: HDDScan (работает в Windows, бесплатная), CrystalDiskInfo (Windows, бесплатная), Hard Disk Sentinel (платная для Windows, бесплатная для DOS), HD Tune (Windows, платная, есть бесплатная старая версия).
И наконец, мощнейшие программы для тестирования: Victoria (Windows, DOS, бесплатная), MHDD (DOS, бесплатная).
Вы ищете память, которая имеет доступ к более высоким скоростям и совместима с большим количеством платформ? Или вы ищете долговечную память, которая может работать 24 часа в сутки, 7 дней в неделю, выявлять больше ошибок, но для этого приходится жертвовать скоростью?
Модули ОЗУ (оперативной памяти) являются важной частью каждой системы, но не все модули одинаковы. Помимо емкости, частоты и задержки, модули могут характеризоваться наличием или отсутствием системы исправления ошибок (ECC).
Разница между ними заключается в том, что память ECC защитит вашу систему от потенциального сбоя, исправив любые ошибки в данных, в то время как память без ECC игнорирует такие ошибки.
Думайте о памяти без ECC как о памяти, ориентированной на скорость, а ECC – памяти, ориентированной на выносливость и надёжности.
Поскольку не все платформы поддерживают ECC-память, и не каждой системе она нужна, давайте обсудим, что такое ECC-память, как она работает и нужна ли она вам.
Что такое ECC-память
Чтобы понять, как работает память с коррекцией ошибок (ECC), сначала нужно понять, что такое однобитовая ошибка. Потому что это основная проблема, для решения которой была создан ECC.
Однобитовая ошибка – это когда один бит (двоичный 0 или 1) в данных в ОЗУ случайно изменяется на противоположное значение.
Такого рода ошибки незначительны, и компьютер может не распознать их автоматически, что может привести ко многим проблемам.
Вы можете думать об однобитовых ошибках как о метафорических сорняках на лужайке. Ваш газон – это оперативная память, а ECC-часть вашей памяти – это использование гербицида.
Память без ECC не избавит вас от «сорняков». ECC уничтожит все сорняки, но газон будет расти немного медленнее.
Однобитовые ошибки могут возникать из-за магнитных или электрических помех внутри компьютера, присутствующих в каждой системе в виде фонового излучения.
Перенапряжение, колебания температуры, удар по корпусу или даже чтение или запись данных не так, как предполагалось изначально, могут привести к однобитовой ошибке.
Память ECC позаботится об этих ошибках и исправит их до того, как они превратятся в большую проблему.
Память с ECC очень похожа на память без ECC. Самая большая разница между ними заключается в том, что память ECC обычно имеет немного дополнительной памяти, предназначенной исключительно для обеспечения того, чтобы фактическая память работала без ошибок.
ECC – это, по сути, небольшой чип на обычной планке ОЗУ, который гарантирует, что каждый бит данных, который входит и выходит, является именно тем, чем он должен быть.
Что он делает, так это то, что создаёт зашифрованный фрагмент кода из данных, записываемых в основную память, и сохраняет этот код в дополнительном бите памяти. Когда необходимо получить доступ к данным, хранящимся в основной памяти, он создаёт новый код и сравнивает этот фрагмент кода с кодом, который был сгенерирован ранее.
Если он обнаружит, что они оба одинаковы и что данные не были каким-либо образом изменены, он разрешает чтение данных. Но, если он обнаруживает, что новый код отличается от сохраненного кода, он попытается решить проблему, расшифровывая код, чтобы точно определить, в чём заключается ошибка.
Если он не сможет найти ошибку, то, по крайней мере, гарантирует, что вы будете знать, что что-то пошло не так, вместо того, чтобы молча продолжать работать.
Это похоже на сравнение хэшей MD5 при загрузке программы, чтобы убедиться, что вы загружаете именно то, что вам действительно нужно, а не другой мошеннический секретный файл.
Вот почему ECC работает немного медленнее – потому что ему приходится создавать эти дополнительные коды.
Согласно исследованиям, вероятность возникновения такой ошибки составляет одна однобитовая ошибка каждые 14-40 часов на гигабит ОЗУ.
Необходимость исправления ошибок на серверах и рабочих станциях
В системе, используемой для повседневного просмотра и игр, исправление ошибок не является необходимостью. Однако, в мире серверов и профессиональных рабочих станций ставки выше.
Если вы ведёте бизнес, специализирующийся на финансах, однобитовая ошибка может привести к сбою сервера, который потенциально может стереть транзакции с вашего сервера.
Такая ошибка памяти также может привести к ошибке транскрипции данных, что может привести к неправильному размещению десятичного разделителя или изменению числа.
Очевидно, что это наносит ущерб честности и надёжности бизнеса. Если бы вы пошли покупать кошке новую игрушку и в итоге заплатили 1000 рублей вместо 100, это было бы довольно трагично.
Если вы посетили своего врача, и счет составил 56 987 рублей вместо 5945 рублей, вы только что стали жертвой компьютерной ошибки, связанной с ECC. И вы, скорее всего, больше никогда не воспользуетесь их услугами.
Потеря времени – ещё одна проблема, которую может предотвратить память ECC. Если вы визуализируете сложные изображения в высоком разрешении или работаете с моделью глубокого обучения, необходимость начинать заново после нескольких недель обработки из-за некоторых ошибок памяти – это огромная трата времени и денег для вашего бизнеса.
Память ECC необходима и в медицинской промышленности. При уходе за пациентом точность записей имеет решающее значение, и ошибка в одном бите может привести к неправильному диагнозу, что может привести к летальному исходу.
Выбор памяти может создать или уничтожить репутацию бизнеса.
Без памяти ECC не только существует вероятность подобных ошибок, но вы также не узнаете, что они произошли, пока кто-нибудь не просмотрит данные и не найдёт ошибку. А иногда это может быть слишком поздно.
Какие платформы поддерживают память ECC
Что касается серверов, то линейки процессоров Intel Xeon и линейки серверов AMD Epyc поддерживают память ECC. Обратите внимание, что для использования памяти ECC и процессор, и используемая материнская плата должны поддерживать память ECC.
Помните аналогию с газоном и гербицидом? Думайте о процессоре и материнской плате как об инструментах, которые вы используете для эффективной работы с ECC. Вам нужны подходящие инструменты для распространения гербицидов на газоне.
На основных платформах, используемых сегодня, большинство процессоров Intel (даже некоторые бюджетные модели Celeron) будут поддерживать память ECC, если вы используете материнскую плату, совместимую с такой памятью.
С AMD все процессоры Ryzen поддерживают память ECC с совместимой материнской платой с набором микросхем X570, тогда как набор микросхем B550 не поддерживает память ECC с процессорами Ryzen 2000. Процессоры Ryzen со встроенной видеокартой или ускоренным процессором (APU), серии 3000 G и серии 4000 G потребуют от вас использования процессора PRO для поддержки ECC.
Недостатки использования памяти ECC
Наиболее распространенная проблема с памятью ECC – совместимость. Несмотря на то, что большинство современных платформ поддерживают её, вы должны убедиться, что конкретная комбинация процессора и материнской платы работает с памятью ECC.
Это менее проблематично в мире серверов, где обычно используется память ECC. Серверное оборудование обычно поддерживает ECC по умолчанию.
Ценник тоже отличается. Модули памяти с ECC дороже, чем модули без ECC из-за дополнительных функций. В зависимости от емкости, которую вы покупаете, разница в цене составляет около 10-20%.
Также наблюдается небольшой спад производительности из-за дополнительного времени, которое требуется памяти ECC для проверки наличия ошибок. По словам Corsair, можно ожидать падения около 2%.
Подведение итогов – нужна ли вам память ECC
Когда вы создаете профессиональную рабочую станцию или сервер, который должен работать круглосуточно и без выходных, память ECC просто необходима.
Обойтись без ECC в этом сценарии было бы все равно, что использовать борзую, чтобы тянуть повозку, когда вам нужна крепкая рабочая лошадка.
И разница в цене, и снижение производительности того стоят, если учесть, что вам не придётся беспокоиться о возможности однобитовой ошибки, которая вызовет у вас головную боль.
Вы ведь не хотели бы перепроверять каждую квитанцию, чтобы убедиться, что она верна, верно? Проявите такую же любезность к своим клиентам и заказчикам.
Но если всё, что вы делаете, это играете в игры и используете свой компьютер для другой некритической работы, вам, скорее всего, не понадобится ECC, и вам важнее сохранить эти 2% производительности.
«Перемежитель» перенаправляется сюда. Для оптоволоконного устройства см. Оптический перемежитель .
В вычислительной , телекоммуникационной , теории информации и теории кодирования , в код коррекции ошибок , иногда кода коррекции ошибок ( ECC ) используется для контроля ошибок в данных по ненадежным или зашумленных каналов связи . Основная идея заключается в том, что отправитель кодирует сообщение с избыточной информацией в форме ECC. Избыточность позволяет получателю обнаруживать ограниченное количество ошибок, которые могут возникнуть в любом месте сообщения, и часто исправлять эти ошибки без повторной передачи. Американский математик Ричард Хэмминг был пионером в этой области в 1940-х годах и изобрел первый исправляющий ошибки код в 1950 году: код Хэмминга (7,4) .
ECC отличается от обнаружения ошибок тем, что обнаруженные ошибки можно исправлять, а не просто обнаруживать. Преимущество состоит в том, что системе, использующей ECC, не требуется обратный канал для запроса повторной передачи данных при возникновении ошибки. Обратной стороной является то, что к сообщению добавляются фиксированные накладные расходы, что требует большей полосы пропускания прямого канала. Таким образом, ECC применяется в ситуациях, когда повторные передачи являются дорогостоящими или невозможными, например, при односторонних каналах связи и при многоадресной передаче на несколько приемников . Соединения с большой задержкой также выигрывают; в случае спутника, вращающегося вокруг Урана , повторная передача из-за ошибок может вызвать задержку в пять часов. Информация ECC обычно добавляется к запоминающим устройствам для восстановления поврежденных данных, широко используется в модемах и используется в системах, где первичной памятью является память ECC .
Обработка ECC в приемнике может применяться к цифровому потоку битов или при демодуляции несущей с цифровой модуляцией. Для последнего ECC является неотъемлемой частью начального аналого-цифрового преобразования в приемнике. Декодер Витерби реализует алгоритм мягкого решения для демодуляции цифровых данных из аналогового сигнала на фоне шума. Многие кодеры / декодеры ECC могут также генерировать сигнал частоты ошибок по битам (BER), который можно использовать в качестве обратной связи для точной настройки аналоговой принимающей электроники.
Максимальная доля ошибок или пропущенных битов, которые могут быть исправлены, определяется конструкцией кода ECC, поэтому разные коды исправления ошибок подходят для разных условий. Как правило, более сильный код вызывает большую избыточность, которую необходимо передавать с использованием доступной полосы пропускания, что снижает эффективную скорость передачи данных при одновременном улучшении принимаемого эффективного отношения сигнал / шум. Кодирования шумным канала теорема о Клода Шеннона может быть использована для вычисления максимальной достижимой пропускной способности канала связи для заданной максимальной допустимой вероятности ошибки. Это устанавливает границы теоретической максимальной скорости передачи информации канала с некоторым заданным базовым уровнем шума. Однако это доказательство неконструктивно и, следовательно, не дает представления о том, как создать код, обеспечивающий производительность. После многих лет исследований некоторые передовые системы ECC по состоянию на 2016 год очень близко подошли к теоретическому максимуму.
Прямое исправление ошибок
В связи , теории информации и теории кодирования , с прямым исправлением ошибок ( FEC ) или канального кодирования является метод , используемый для контроля ошибок в передаче данных по ненадежным или зашумленных каналов связи . Основная идея состоит в том, что отправитель кодирует сообщение избыточным способом, чаще всего с помощью ECC.
Избыточность позволяет получателю обнаруживать ограниченное количество ошибок, которые могут возникнуть в любом месте сообщения, и часто исправлять эти ошибки без повторной передачи. FEC дает приемнику возможность исправлять ошибки без необходимости использования обратного канала для запроса повторной передачи данных, но за счет фиксированной более высокой полосы пропускания прямого канала. Поэтому FEC применяется в ситуациях, когда повторная передача является дорогостоящей или невозможной, например, при односторонних каналах связи и при передаче на несколько приемников в многоадресной передаче . Информация FEC обычно добавляется в устройства массовой памяти (магнитные, оптические и твердотельные / флеш-накопители), чтобы обеспечить восстановление поврежденных данных, широко используется в модемах , используется в системах, где первичной памятью является память ECC, и в ситуациях вещания, где приемник не имеет возможности запрашивать повторную передачу, иначе это может вызвать значительную задержку. Например, в случае спутника, вращающегося вокруг Урана , повторная передача из-за ошибок декодирования может вызвать задержку не менее 5 часов.
Обработка FEC в приемнике может применяться к цифровому битовому потоку или при демодуляции несущей с цифровой модуляцией. Для последнего FEC является неотъемлемой частью начального аналого-цифрового преобразования в приемнике. Декодер Витерби реализует алгоритм мягкого решения для демодуляции цифровых данных из аналогового сигнала на фоне шума. Многие кодеры FEC могут также генерировать сигнал частоты ошибок по битам (BER), который можно использовать в качестве обратной связи для точной настройки аналоговой приемной электроники.
Максимальная доля ошибок или недостающих битов, которые могут быть исправлены, определяется конструкцией ECC, поэтому разные коды прямого исправления ошибок подходят для разных условий. Как правило, более сильный код вызывает большую избыточность, которую необходимо передавать с использованием доступной полосы пропускания, что снижает эффективную скорость передачи данных при одновременном улучшении принимаемого эффективного отношения сигнал / шум. Шумная-канальное кодирование теоремы Клод Шеннон отвечает на вопрос о том, сколько трафика остался для передачи данных при использовании наиболее эффективного кода , который превращает вероятность ошибки декодирования к нулю. Это устанавливает границы теоретической максимальной скорости передачи информации канала с некоторым заданным базовым уровнем шума. Его доказательство неконструктивно и, следовательно, не дает представления о том, как создать код, обеспечивающий производительность. Однако после многих лет исследований некоторые продвинутые системы FEC, такие как полярный код, достигают пропускной способности канала Шеннона в рамках гипотезы кадра бесконечной длины.
Как это работает
ECC достигается путем добавления избыточности к передаваемой информации с использованием алгоритма. Избыточный бит может быть сложной функцией многих исходных информационных битов. Исходная информация может появляться или не появляться буквально в закодированном выводе; коды, которые включают немодифицированный ввод в вывод, являются систематическими , тогда как те, которые не включают, являются несистематичными .
Упрощенный пример ECC — это передача каждого бита данных 3 раза, что известно как код повторения (3,1) . Через шумный канал приемник может видеть 8 версий вывода, см. Таблицу ниже.
| Триплет получил | Интерпретируется как |
|---|---|
| 000 | 0 (без ошибок) |
| 001 | 0 |
| 010 | 0 |
| 100 | 0 |
| 111 | 1 (без ошибок) |
| 110 | 1 |
| 101 | 1 |
| 011 | 1 |
Это позволяет исправить ошибку в любой из трех выборок «большинством голосов» или «демократическим голосованием». Корректирующая способность этого ECC:
- Ошибка до 1 бита триплета, или
- пропущено до 2 битов триплета (случаи не указаны в таблице).
Хотя эта тройная модульная избыточность проста в реализации и широко используется, она является относительно неэффективной ECC. Более совершенные коды ECC обычно проверяют последние несколько десятков или даже несколько последних сотен ранее принятых битов, чтобы определить, как декодировать текущую небольшую группу битов (обычно в группах от 2 до 8 бит).
Усреднение шума для уменьшения ошибок
Можно сказать, что ECC работает путем «усреднения шума»; поскольку каждый бит данных влияет на многие передаваемые символы, искажение одних символов шумом обычно позволяет извлекать исходные пользовательские данные из других, неповрежденных принятых символов, которые также зависят от тех же пользовательских данных.
- Из-за этого эффекта «объединения рисков» цифровые системы связи, использующие ECC, как правило, работают значительно выше определенного минимального отношения сигнал / шум, а вовсе не ниже него.
- Эта тенденция «все или ничего» — эффект обрыва — становится более выраженным по мере использования более сильных кодов, которые ближе подходят к теоретическому пределу Шеннона .
- Перемежение данных, закодированных с помощью ЕСС, может уменьшить свойства «все или ничего» передаваемых кодов ЕСС, когда ошибки канала имеют тенденцию возникать в пакетах. Однако у этого метода есть ограничения; его лучше всего использовать для узкополосных данных.
Большинство систем электросвязи используют код фиксированного канала, рассчитанный на то, чтобы выдерживать ожидаемую частоту ошибок по битам в наихудшем случае , а затем вообще не работают, если частота ошибок по битам становится еще хуже. Однако некоторые системы адаптируются к заданным условиям ошибки канала: некоторые экземпляры гибридного автоматического запроса на повторение используют фиксированный метод ECC, пока ECC может обрабатывать частоту ошибок, а затем переключаются на ARQ, когда частота ошибок становится слишком высокой;
адаптивная модуляция и кодирование используют различные скорости ECC, добавляя больше битов исправления ошибок на пакет, когда в канале более высокие частоты ошибок, или удаляя их, когда они не нужны.
Типы ECC
Краткая классификация кодов исправления ошибок
Двумя основными категориями кодов ECC являются блочные коды и сверточные коды .
- Блочные коды работают с блоками (пакетами) фиксированного размера, состоящими из битов или символов заранее определенного размера. Практические блочные коды обычно могут быть жестко декодированы за полиномиальное время до их длины блока.
- Сверточные коды работают с битовыми или символьными потоками произвольной длины. Чаще всего они декодируются с помощью алгоритма Витерби , хотя иногда используются и другие алгоритмы. Декодирование Витерби обеспечивает асимптотически оптимальную эффективность декодирования с увеличением длины ограничения сверточного кода, но за счет экспоненциально возрастающей сложности. Завершенный сверточный код также является «блочным кодом» в том смысле, что он кодирует блок входных данных, но размер блока сверточного кода, как правило, произвольный, в то время как блочные коды имеют фиксированный размер, определяемый их алгебраическими характеристиками. Типы завершения для сверточных кодов включают «концевую передачу» и «сброс битов».
Есть много типов блочных кодов; Кодирование Рида-Соломона примечательно тем, что оно широко используется на компакт-дисках , DVD и жестких дисках . К другим примерам классических блочных кодов относятся коды Голея , BCH , многомерная четность и коды Хэмминга .
ECC Хэмминга обычно используется для исправления ошибок флэш- памяти NAND . Это обеспечивает исправление однобитовых ошибок и обнаружение двухбитовых ошибок. Коды Хэмминга подходят только для более надежной одноуровневой ячейки (SLC) NAND. Более плотная многоуровневая ячейка (MLC) NAND может использовать многобитовый корректирующий ECC, такой как BCH или Reed-Solomon. NOR Flash обычно не использует никаких исправлений ошибок.
Классические блочные коды обычно декодируются с использованием алгоритмов жесткого решения , что означает, что для каждого входного и выходного сигнала принимается жесткое решение, соответствует ли он единице или нулю. Напротив, сверточные коды обычно декодируются с использованием алгоритмов мягкого решения , таких как алгоритмы Витерби, MAP или BCJR , которые обрабатывают (дискретизированные) аналоговые сигналы и которые обеспечивают гораздо более высокую производительность исправления ошибок, чем декодирование с жестким решением.
Почти все классические блочные коды применяют алгебраические свойства конечных полей . Поэтому классические блочные коды часто называют алгебраическими кодами.
В отличие от классических блочных кодов, которые часто определяют способность обнаружения или исправления ошибок, многие современные блочные коды, такие как коды LDPC, не имеют таких гарантий. Вместо этого современные коды оцениваются с точки зрения их частоты ошибок по битам.
Большинство кодов прямого исправления ошибок исправляют только перевороты битов, но не вставки или удаления битов. В этом случае расстояние Хэмминга является подходящим способом измерения частоты ошибок по битам . Несколько кодов прямого исправления ошибок предназначены для исправления вставки и удаления битов, например, коды маркеров и коды водяных знаков. Расстояние Левенштейна — более подходящий способ измерения частоты ошибок по битам при использовании таких кодов.
Кодовая скорость и компромисс между надежностью и скоростью передачи данных
Основным принципом ECC является добавление избыточных битов, чтобы помочь декодеру узнать истинное сообщение, закодированное передатчиком. Кодовая скорость данной системы ЕСС определяется как отношение между количеством информационных битов и общим количеством битов (т. Е. Информация плюс биты избыточности) в данном коммуникационном пакете. Кодовая скорость, следовательно, является действительным числом. Низкая кодовая скорость, близкая к нулю, подразумевает сильный код, который использует много избыточных битов для достижения хорошей производительности, в то время как большая кодовая скорость, близкая к 1, подразумевает слабый код.
Избыточные биты, защищающие информацию, должны передаваться с использованием тех же коммуникационных ресурсов, которые они пытаются защитить. Это вызывает принципиальный компромисс между надежностью и скоростью передачи данных. В одном крайнем случае сильный код (с низкой кодовой скоростью) может вызвать значительное увеличение SNR приемника (отношение сигнал / шум), уменьшая частоту ошибок по битам, за счет снижения эффективной скорости передачи данных. С другой стороны, без использования какого-либо ECC (т. Е. Кодовая скорость, равная 1), используется полный канал для целей передачи информации за счет того, что биты остаются без какой-либо дополнительной защиты.
Один интересный вопрос заключается в следующем: насколько эффективным с точки зрения передачи информации может быть ECC, имеющий незначительную частоту ошибок декодирования? На этот вопрос ответил Клод Шеннон с его второй теоремой, в которой говорится, что пропускная способность канала — это максимальная скорость передачи данных, достижимая для любого ECC, частота ошибок которого стремится к нулю: его доказательство опирается на гауссовское случайное кодирование, которое не подходит для реального мира. Приложения. Верхняя граница, заданная работой Шеннона, вдохновила на долгий путь к разработке ECC, которые могут приблизиться к конечной границе производительности. Различные коды сегодня могут достигать почти предела Шеннона. Однако ECC, обеспечивающие пропускную способность, обычно чрезвычайно сложно реализовать.
Самые популярные ECC имеют компромисс между производительностью и вычислительной сложностью. Обычно их параметры дают диапазон возможных кодовых скоростей, которые можно оптимизировать в зависимости от сценария. Обычно эта оптимизация выполняется для достижения низкой вероятности ошибки декодирования при минимальном влиянии на скорость передачи данных. Другим критерием оптимизации кодовой скорости является уравновешивание низкой частоты ошибок и количества повторных передач с учетом затрат энергии на связь.
Составные коды ECC для повышения производительности
Классические (алгебраические) блочные коды и сверточные коды часто комбинируются в схемах конкатенированного кодирования, в которых сверточный код, декодированный по Витерби с короткой ограниченной длиной, выполняет большую часть работы, а блочный код (обычно Рида-Соломона) с большим размером символа и длиной блока «стирает» любые ошибки, сделанные сверточным декодером. Однопроходное декодирование с помощью этого семейства кодов с исправлением ошибок может дать очень низкий уровень ошибок, но для условий передачи на большие расстояния (например, в глубоком космосе) рекомендуется итеративное декодирование.
Составные коды стали стандартной практикой в спутниковой связи и связи в дальнем космосе с тех пор, как « Вояджер-2» впервые применил эту технику во время своей встречи с Ураном в 1986 году . Аппарат Galileo использовал итеративные сцепленные коды для компенсации условий очень высокой частоты ошибок, вызванных неисправной антенной.
Проверка четности с низкой плотностью (LDPC)
Коды с низкой плотностью проверки на четность (LDPC) представляют собой класс высокоэффективных линейных блочных кодов, состоящих из множества кодов одиночной проверки на четность (SPC). Они могут обеспечить производительность, очень близкую к пропускной способности канала (теоретический максимум), используя подход итеративного декодирования с мягким решением, при линейной временной сложности с точки зрения длины их блока. Практические реализации в значительной степени полагаются на параллельное декодирование составляющих кодов SPC.
Коды LDPC были впервые представлены Робертом Г. Галлагером в его докторской диссертации в 1960 году, но из-за вычислительных усилий при реализации кодировщика и декодера и введения кодов Рида-Соломона они в основном игнорировались до 1990-х годов.
Коды LDPC теперь используются во многих последних стандартах высокоскоростной связи, таких как DVB-S2 (цифровое видеовещание — спутниковое — второе поколение), WiMAX ( стандарт IEEE 802.16e для микроволновой связи), высокоскоростная беспроводная локальная сеть ( IEEE 802.11n). ), 10GBase-T Ethernet (802.3an) и G.hn/G.9960 (стандарт ITU-T для сетей по линиям электропередач, телефонным линиям и коаксиальному кабелю). Другие коды LDPC стандартизированы для стандартов беспроводной связи в рамках 3GPP MBMS (см. Исходные коды ).
Турбо коды
Турбокодирование — это итеративная схема мягкого декодирования, которая объединяет два или более относительно простых сверточных кода и перемежитель для создания блочного кода, который может работать с точностью до доли децибела от предела Шеннона . Предваряя коды LDPC с точки зрения практического применения, теперь они обеспечивают аналогичную производительность.
Одним из первых коммерческих приложений турбо-кодирования была технология цифровой сотовой связи CDMA2000 1x (TIA IS-2000), разработанная Qualcomm и продаваемая Verizon Wireless , Sprint и другими операторами связи. Он также используется для развития CDMA2000 1x специально для доступа в Интернет, 1xEV-DO (TIA IS-856). Как и 1x, EV-DO был разработан Qualcomm и продается Verizon Wireless , Sprint и другими операторами (маркетинговое название Verizon для 1xEV-DO — широкополосный доступ , потребительские и бизнес-маркетинговые названия Sprint для 1xEV-DO — Power Vision и Mobile. Широкополосный соответственно).
Локальное декодирование и тестирование кодов
Иногда необходимо декодировать только отдельные биты сообщения или проверить, является ли данный сигнал кодовым словом, и сделать это, не глядя на весь сигнал. Это может иметь смысл в настройке потоковой передачи, где кодовые слова слишком велики, чтобы их можно было классически декодировать достаточно быстро, и где на данный момент интересны только несколько битов сообщения. Также такие коды стали важным инструментом в теории сложности вычислений , например, для разработки вероятностно проверяемых доказательств .
Локально декодируемые коды — это коды с исправлением ошибок, для которых отдельные биты сообщения могут быть вероятностно восстановлены, если смотреть только на небольшое (скажем, постоянное) количество позиций кодового слова, даже после того, как кодовое слово было искажено в некоторой постоянной доле позиций. Локально тестируемые коды — это коды с исправлением ошибок, для которых можно вероятностно проверить, близок ли сигнал к кодовому слову, только посмотрев на небольшое количество позиций сигнала.
Чередование
«Перемежитель» перенаправляется сюда. Для оптоволоконного устройства см. Оптический перемежитель .
Краткая иллюстрация идеи чередования
Перемежение часто используется в системах цифровой связи и хранения для повышения производительности кодов прямого исправления ошибок. Многие каналы связи не лишены памяти: ошибки обычно возникают пакетами, а не независимо друг от друга. Если количество ошибок в кодовом слове превышает возможности кода исправления ошибок, ему не удается восстановить исходное кодовое слово. Чередование облегчает эту проблему, перетасовывая исходные символы по нескольким кодовым словам, тем самым создавая более равномерное распределение ошибок. Поэтому перемежение широко используется для исправления пакетных ошибок .
Анализ современных итеративных кодов, как турбо — коды и LDPC — коды , как правило , предполагает независимое распределение ошибок. Поэтому системы, использующие коды LDPC, обычно используют дополнительное перемежение символов в кодовом слове.
Для турбокодов перемежитель является неотъемлемым компонентом, и его правильная конструкция имеет решающее значение для хорошей производительности. Алгоритм итеративного декодирования работает лучше всего, когда в графе факторов , представляющем декодер , нет коротких циклов ; перемежитель выбран, чтобы избежать коротких циклов.
Конструкции перемежителя включают:
- прямоугольные (или однородные) перемежители (аналогично методу с использованием коэффициентов пропуска, описанному выше)
- сверточные перемежители
- случайные перемежители (где перемежитель — известная случайная перестановка)
- S-случайный перемежитель (где перемежитель — это известная случайная перестановка с ограничением, что никакие входные символы на расстоянии S не появляются на расстоянии S на выходе).
- бесконкурентный квадратичный многочлен с перестановками (QPP). Пример использования — стандарт мобильной связи 3GPP Long Term Evolution .
В системах связи с множеством несущих перемежение по несущим может использоваться для обеспечения частотного разнесения , например, для уменьшения частотно-избирательного замирания или узкополосных помех.
Пример
Передача без чередования :
Error-free message: aaaabbbbccccddddeeeeffffgggg Transmission with a burst error: aaaabbbbccc____deeeeffffgggg
Здесь каждая группа одинаковых букв представляет собой 4-битное однобитовое кодовое слово с исправлением ошибок. Кодовое слово cccc изменяется в один бит и может быть исправлено, но кодовое слово dddd изменяется в трех битах, поэтому либо оно не может быть декодировано вообще, либо может быть декодировано неправильно .
С чередованием :
Error-free code words: aaaabbbbccccddddeeeeffffgggg Interleaved: abcdefgabcdefgabcdefgabcdefg Transmission with a burst error: abcdefgabcd____bcdefgabcdefg Received code words after deinterleaving: aa_abbbbccccdddde_eef_ffg_gg
В каждом из кодовых слов «aaaa», «eeee», «ffff» и «gggg» изменяется только один бит, поэтому однобитовый код с исправлением ошибок все декодирует правильно.
Передача без чередования :
Original transmitted sentence: ThisIsAnExampleOfInterleaving Received sentence with a burst error: ThisIs______pleOfInterleaving
Термин «пример» в большинстве случаев оказывается непонятным и трудным для исправления.
С чередованием :
Transmitted sentence: ThisIsAnExampleOfInterleaving... Error-free transmission: TIEpfeaghsxlIrv.iAaenli.snmOten. Received sentence with a burst error: TIEpfe______Irv.iAaenli.snmOten. Received sentence after deinterleaving: T_isI_AnE_amp_eOfInterle_vin_...
Ни одно слово не потеряно полностью, а недостающие буквы можно восстановить с минимальными догадками.
Недостатки чередования
Использование методов чередования увеличивает общую задержку. Это связано с тем, что перед декодированием пакетов должен быть принят весь чередующийся блок. Также перемежители скрывают структуру ошибок; без перемежителя более совершенные алгоритмы декодирования могут использовать структуру ошибок и обеспечивать более надежную связь, чем более простой декодер, объединенный с перемежителем. Пример такого алгоритма основан на структурах нейронной сети .
Программное обеспечение для кодов исправления ошибок
Моделирование поведения кодов исправления ошибок (ECC) в программном обеспечении — обычная практика для разработки, проверки и улучшения ECC. Предстоящий стандарт беспроводной связи 5G поднимает новый диапазон приложений для программных ECC: облачные сети радиодоступа (C-RAN) в контексте программно-определяемого радио (SDR) . Идея состоит в том, чтобы напрямую использовать программные ECC в коммуникациях. Например, в 5G программные ECC могут быть расположены в облаке, а антенны подключены к этим вычислительным ресурсам: таким образом повышается гибкость сети связи и, в конечном итоге, повышается энергоэффективность системы.
В этом контексте существует различное доступное программное обеспечение с открытым исходным кодом, перечисленное ниже (не является исчерпывающим).
- AFF3CT (A Fast Forward Error Correction Toolbox): полная коммуникационная цепочка на C ++ (многие поддерживаемые коды, такие как Turbo, LDPC, полярные коды и т. Д.), Очень быстрая и специализированная на канальном кодировании (может использоваться как программа для моделирования или как библиотека для SDR).
- IT ++ : библиотека классов и функций C ++ для линейной алгебры, численной оптимизации, обработки сигналов, связи и статистики.
- OpenAir : реализация (на языке C) спецификаций 3GPP, касающихся Evolved Packet Core Networks.
Список кодов исправления ошибок
| Расстояние | Код |
|---|---|
| 2 (обнаружение одиночной ошибки) | Паритет |
| 3 (исправление одиночных ошибок) | Тройное модульное резервирование |
| 3 (исправление одиночных ошибок) | идеальный Хэмминга, такой как Хэмминга (7,4) |
| 4 ( ВТОРОЕ ) | Расширенный Хэмминга |
| 5 (исправление двойной ошибки) | |
| 6 (исправление двойной ошибки / обнаружение тройной ошибки) | |
| 7 (исправление трех ошибок) | совершенный двоичный код Голея |
| 8 (ТЕКФЕД) | расширенный двоичный код Голея |
- Коды AN
- Код BCH , который может быть разработан для исправления произвольного количества ошибок в каждом блоке кода.
- Код Бергера
- Код постоянного веса
- Сверточный код
- Коды расширителей
- Групповые коды
- Коды Голея , из которых двоичный код Голея представляет практический интерес.
- Код Гоппа , используемый в криптосистеме Мак-Элиса
- Код Адамара
- Код Хагельбаргера
- Код Хэмминга
- Код на основе латинского квадрата для небелого шума (преобладающий, например, в широкополосной связи по линиям электропередач)
- Лексикографический код
- Линейное сетевое кодирование , тип кода с исправлением стирания в сетях вместо двухточечных ссылок
- Длинный код
- Код проверки на четность с низкой плотностью , также известный как код Галлагера , как архетип для кодов разреженных графов
- Код LT , который является почти оптимальным кодом бесскоростной коррекции стирания (код Фонтана)
- m из n кодов
- Онлайн-код , почти оптимальный код бесскоростной коррекции стирания
- Полярный код (теория кодирования)
- Код Raptor , почти оптимальный код бесскоростной коррекции стирания
- Исправление ошибок Рида – Соломона
- Код Рида – Мюллера
- Повторно-накопительный код
- Коды повторения , такие как тройное модульное резервирование
- Спинальный код, бесскоростной нелинейный код, основанный на псевдослучайных хэш-функциях
- Код Торнадо , почти оптимальный код коррекции стирания и предшественник кодов Фонтана
- Турбо код
- Код Уолша-Адамара
-
Циклические проверки избыточности (CRC) могут исправлять 1-битные ошибки для сообщений длиной не более бит для оптимальных порождающих полиномов степени , см. Математика циклических проверок избыточности # Битовые фильтры
Смотрите также
- Скорость кода
- Коды стирания
- Декодер мягкого решения
- Пакетный код исправления ошибок
- Обнаружение и исправление ошибок
- Коды исправления ошибок с обратной связью
использованная литература
дальнейшее чтение
- МакВильямс, Флоренс Джессим ; Слоан, Нил Джеймс Александр (2007) [1977]. Написано в AT&T Shannon Labs, Флорхэм-Парк, Нью-Джерси, США. Теория кодов, исправляющих ошибки . Математическая библиотека Северной Голландии. 16 (цифровой отпечаток 12-го оттиска, 1-е изд.). Амстердам / Лондон / Нью-Йорк / Токио: Северная Голландия / Elsevier BV . ISBN 978-0-444-85193-2. LCCN 76-41296 . (xxii + 762 + 6 страниц)
- Кларк младший, Джордж К.; Каин, Дж. Бибб (1981). Кодирование с коррекцией ошибок для цифровой связи . Нью-Йорк, США: Plenum Press . ISBN 0-306-40615-2.
- Арази, Бенджамин (1987). Swetman, Herb (ред.). Здравый подход к теории кодов, исправляющих ошибки . Серия MIT Press в компьютерных системах. 10 (1-е изд.). Кембридж, Массачусетс, США / Лондон, Великобритания: Массачусетский технологический институт . ISBN 0-262-01098-4. LCCN 87-21889 . (x + 2 + 208 + 4 страницы)
- Плетеный, Стивен Б. (1995). Системы контроля ошибок для цифровой связи и хранения . Энглвуд Клиффс, Нью-Джерси, США: Прентис-Холл . ISBN 0-13-200809-2.
- Уилсон, Стивен Г. (1996). Цифровая модуляция и кодирование . Энглвуд Клиффс, Нью-Джерси, США: Прентис-Холл . ISBN 0-13-210071-1.
- «Код коррекции ошибок в флеш-памяти NAND с одноуровневой ячейкой» 2007-02-16
- «Код исправления ошибок во флеш-памяти NAND» 2004-11-29
- Наблюдения за ошибками, исправлениями и доверием зависимых систем , Джеймс Гамильтон, 26 февраля 2012 г.
- Сферические упаковки, решетки и группы, Дж. Х. Конвей, Нил Джеймс Александр Слоан, Springer Science & Business Media , 2013-03-09 — Математика — 682 страницы.
внешние ссылки
- Морелос-Сарагоса, Роберт (2004). «Страница корректирующих кодов (ECC)» . Проверено 5 марта 2006 года .
- lpdec: библиотека для декодирования LP и связанных вещей (Python)
Контроль четности и коды коррекции ошибок (ECC).
Ошибки при хранении информации в памяти неизбежны. Они обычно классифицируются как отказы и нерегулярные ошибки (сбои). Если нормально функционирующая микросхема вследствие, например, физического повреждения начинает работать неправильно, то все происходящее и называется постоянным отказом. Чтобы устранить этот тип отказа, обычно требуется заменить некоторую часть аппаратных средств памяти, например неисправную микросхему памяти.
Другой, более коварный тип отказа — нерегулярная ошибка (сбой). Это непостоянный отказ, который не происходит при повторении условий функционирования или через регулярные интервалы.
Приблизительно 20 лет назад сотрудники Intel установили, что причиной сбоев являются альфа-частицы. Поскольку альфа-частицы не могут проникнуть даже через тонкий лист бумаги, выяснилось, что их источником служит вещество, используемое в полупроводниках. При исследовании были обнаружены частицы тория и урана в пластмассовых и керамических корпусах микросхем, применявшихся в те годы. Изменив технологический процесс, производители памяти избавились от этих примесей.
В настоящее время производители памяти почти полностью устранили источники альфачастиц. И многие стали думать, что проверка четности не нужна вовсе. Например, сбои в памяти емкостью 16 Мбайт из-за альфа-частиц случаются в среднем только один раз за 16 лет! Однако сбои памяти происходят значительно чаще.
Сегодня самая главная причина нерегулярных ошибок — космические лучи. Поскольку они имеют очень большую проникающую способность, от них практически нельзя защититься с помощью экранирования.
Эксперимент, проверяющий степень влияния космических лучей на появление ошибок в работе микросхем, показал, что соотношение “сигнал–ошибка” (signal-to-error ratio — SER) для некоторых модулей DRAM составило 5950 единиц интенсивности отказов (failure units — FU) на миллиард часов наработки для каждой микросхемы. Измерения проводились в условиях, приближенных к реальной жизни, с учетом длительности в несколько миллионов машиночасов. В среднестатистическом компьютере это означало бы появление программной ошибки памяти примерно каждые шесть месяцев. В серверных системах или мощных рабочих станциях с большим объемом установленной оперативной памяти подобная статистика указывает на одну ошибку (или даже более) в работе памяти каждый месяц! Когда тестовая система с теми же модулями DIMM была размещена в надежном убежище на глубине более 15 метров каменной породы, что полностью устраняет влияние космических лучей, программные ошибки в работе памяти вообще не были зафиксированы. Эксперимент продемонстрировал не только опасность влияния космических лучей, но и доказал, насколько эффективно устранять влияние альфалучей и радиоактивных примесей в оболочках модулей памяти.
К сожалению, производители ПК не признали это причиной погрешностей памяти; случайную природу сбоя намного легче оправдать разрядом электростатического электричества, большими выбросами мощности или неустойчивой работой программного обеспечения (например, использованием новой версии операционной системы или большой прикладной программы). Исследования показали, что для систем ECC доля программных ошибок в 30 раз больше, чем аппаратных. Это неудивительно, учитывая вредное влияние космических лучей. Количество ошибок зависит от числа установленных модулей памяти и их объема. Программные ошибки могут случаться и раз в месяц, и несколько раз в неделю, и даже чаще!
Хотя космические лучи и радиация являются причиной большинства программных ошибок памяти, существуют и другие факторы:
1. Скачки в энергопотреблении или шум на линии. Причиной может быть неисправный блок питания или настенная розетка.
2. Использование неверного типа или параметра быстродействия памяти. Тип памяти
должен поддерживаться конкретным набором микросхем и обладать определенной
этим набором скоростью доступа.
3. Электромагнитные помехи. Возникают при расположении радиопередатчиков рядом с
компьютером, что иногда приводит к генерированию паразитных электрических сигна-
лов в монтажных соединениях и схемах компьютера. Имейте в виду, что беспроводные
сети, мыши и клавиатуры увеличивают риск появления электромагнитных помех.
4. Статические разряды. Вызывают моментальные скачки в энергоснабжении, что может
повлиять на целостность данных.
5. Ошибки синхронизации. Не поступившие своевременно данные могут стать причиной
появления программных ошибок. Зачастую причина заключается в неверных парамет-
рах BIOS, оперативной памяти, быстродействие которой ниже, чем требуется систе-
мой, “разогнанных” процессорах и прочих системных компонентах.
Большинство описанных проблем не приводят к прекращению работы микросхем памяти (хотя некачественное энергоснабжение или статическое электричество могут физически повредить микросхемы), однако могут повлиять на хранимые данные.
Игнорирование сбоев, конечно, не лучший способ борьбы с ними. К сожалению, именно этот способ сегодня выбрали многие производители компьютеров. Лучше было бы повысить отказоустойчивость систем. Для этого необходимы механизмы определения и, возможно, исправления ошибок в памяти ПК. В основном для повышения отказоустойчивости в современных компьютерах применяются следующие методы:
— контроль четности;
— коды коррекции ошибок (ECC).
Системы без контроля четности вообще не обеспечивают отказоустойчивости данных. Единственная причина, по которой они используются, — их минимальная базовая стоимость. При этом, в отличие от других технологий (ECC и контроль четности), не требуется дополнительная оперативная память.
Байт данных с контролем четности включает в себя 9, а не 8 бит, поэтому стоимость памяти с контролем четности выше примерно на 12,5%. Кроме того, контроллеры памяти, не требующие логических мостов для подсчета данных четности или ECC, обладают упрощенной внутренней архитектурой. Портативные системы, для которых вопрос минимального энергопотребления особенно важен, выигрывают от уменьшенного энергопотребления памяти благодаря использованию меньшего количества микросхем DRAM. И наконец, шина данных памяти без контроля четности имеет меньшую разрядность, что выражается в сокращении количества буферов данных. Статистическая вероятность возникновения ошибок памяти в современных настольных компьютерах составляет примерно одну ошибку в несколько месяцев. При этом количество ошибок зависит от объема и типа используемой памяти. Подобный уровень ошибок может быть приемлемым для обычных компьютеров, не используемых для работы с важными приложениями. В этом случае цена играет основную роль, а дополнительная стоимость модулей памяти с поддержкой контроля четности и кода ECC себя не оправдывает.
Применение не отказоустойчивых к ошибкам компьютеров рискованно и предполагает отсутствие ошибок памяти при эксплуатации систем. При этом также учитывается, что совокупная стоимость потерь, вызванная ошибками в работе памяти, будет меньше, чем затраты на приобретение дополнительных аппаратных устройств для определения таковых ошибок.
Тем не менее ошибки памяти вполне могут стать причиной серьезных проблем: например, представьте себе указание неверного значения суммы в банковском чеке. Ошибки в работе оперативной памяти серверных систем зачастую приводят к “зависанию” последних и отключению всех клиентских компьютеров, соединенных с серверами по локальной сети. Наконец, отследить причину возникновения проблем в компьютерах, не поддерживающих контроль четности или код ECC, крайне сложно. Последние технологии по крайней мере однозначно укажут на оперативную память как на источник проблемы, тем самым экономя время и усилия системных администраторов.
Контроль четности
Это один из стандартов, введенных IBM, в соответствии с которым информация в банках памяти хранится фрагментами по девять битов, причем восемь из них (составляющих один байт) предназначены собственно для данных, а девятый является битом четности (parity). Использование девятого бита позволяет схемам управления памятью на аппаратном уровне контролировать целостность каждого байта данных. Если обнаруживается ошибка, работа компьютера останавливается и на экран выводится сообщение о неисправности.
Технология контроля четности не позволяет исправлять системные ошибки, однако дает возможность их обнаружить пользователю компьютера, что имеет следующие преимущества:
— контроль четности оберегает от последствий проведения неверных вычислений на базе некорректных данных;
— контроль четности точно указывает на источник возникновения ошибок, помогая разобраться с проблемой и улучшая степень эксплутационной надежности компьютера.
Для реализации поддержки памяти с контролем четности или без него не требуется особых усилий. В частности, внедрить поддержку контроля четности для системной платы не составит никакого труда. Основная стоимость внедрения относится к цене самих модулей памяти с контролем четности. Если покупатели нуждаются в контроле четности для работы с определенными приложениями, поставщики компьютеров могут без проблем предложить соответствующие системы.
Компания Intel и прочие производители наборов микросхем системной логики внедрили поддержку контроля четности и кода ECC в большинстве своих продуктов (особенно в наборах микросхем, ориентированных на рынок высокопроизводительных серверов). В то же время наборы микросхем низшей ценовой категории, как правило, не поддерживают эти технологии. Пользователям, требовательным к надежности выполняемых приложений, следует обращать особое внимание на поддержку контроля четности и ECC.
Код коррекции ошибок
Коды коррекции ошибок (Error Correcting Code — ECC) позволяют не только обнаружить ошибку, но и исправить ее в одном разряде. Поэтому компьютер, в котором используются подобные коды, в случае ошибки в одном разряде может работать без прерывания, причем данные не будут искажены. Коды коррекции ошибок в большинстве ПК позволяют только обнаруживать, но не исправлять ошибки в двух разрядах. Но приблизительно 98% сбоев памяти вызвано именно ошибкой в одном разряде, т.е. она успешно исправляется с помощью данного типа кодов. Данный тип ECC получил название SEC)DED (single-bit error-correction double-bit error detection — одноразрядная коррекция, двухразрядное обнаружение ошибок). В кодах коррекции ошибок этого типа для каждых 32 бит требуется дополнительно семь контрольных разрядов при 4-байтовой и восемь — при 8-байтовой организации (64-разрядные процессоры Athlon/Pentium). Реализация кода коррекции ошибок при 4-байтовой организации, очевидно, дороже реализации проверки нечетности или четности, но при 8-байтовой организации стоимость реализации кода коррекции ошибок не превышает стоимости реализации проверки четности.
Для использования кодов коррекции ошибок необходим контроллер памяти, вычисляющий контрольные разряды при операции записи в память. При чтении из памяти такой контроллер сравнивает прочитанные и вычисленные значения контрольных разрядов и при необходимости исправляет испорченный бит (или биты). Стоимость дополнительных логических схем для реализации кода коррекции ошибок в контроллере памяти не очень высока, но это может значительно снизить быстродействие памяти при операциях записи. Это происходит потому, что при операциях записи и чтения необходимо ждать, когда завершится вычисление контрольных разрядов. При записи части слова вначале следует прочитать полное слово, затем перезаписать изменяемые байты и только после этого — новые вычисленные контрольные разряды.
В большинстве случаев сбой памяти происходит в одном разряде, и потому такие ошибки успешно исправляются кодом коррекции ошибок. Использование отказоустойчивой памяти обеспечивает высокую надежность компьютера. Память с кодом ECC предназначена для серверов, рабочих станций или приложений, для которых последствия потенциальных ошибок памяти менее желательны, чем дополнительные затраты на приобретение добавочных модулей памяти и вычислительные затраты на коррекцию ошибок. Если данные имеют особое значение и компьютеры применяются для решения важных задач, без памяти ECC не обойтись. По сути, ни один уважающий себя системный инженер не будет использовать сервер, даже самый неприхотливый, без памяти ECC.
Пользователи имеют выбор между системами без контроля четности, с контролем четности и с ECC, т.е. между желательным уровнем отказоустойчивости компьютера и степенью ценности используемых данных.