Эквивалентный радиус рассеивания ошибок измерений в икс дин - Oshibki.top

Для
приближенного учета рефракции вводят
понятие эквивалентного радиуса Земли
а_э,
справедливое при линейном изменении ε
с
высотой.
В действительности в тропосфере в
среднем ε убывает с высотой по
экспоненциальному закону. Но для
сравнительно тонких слоев, к которым
можно отнести приземный слой, участвующий
в переносе энергии на трассах РРЛ, это
упрощение допустимо.

Под величиной
а_э
понимают
такое значение радиуса Земли, при котором
траектории радиоволн можно считать
прямолинейными, причем

а_э
= а
/
(1 + аg
/
2), (2.16)

где а
=
6370 км — геометрический, радиус Земли.
При g=0:
а_э
= а,
т. е. рефракция отсутствует. На практике
часто применяют понятие коэффициента
рефракции

K_э
=
а_э/а.

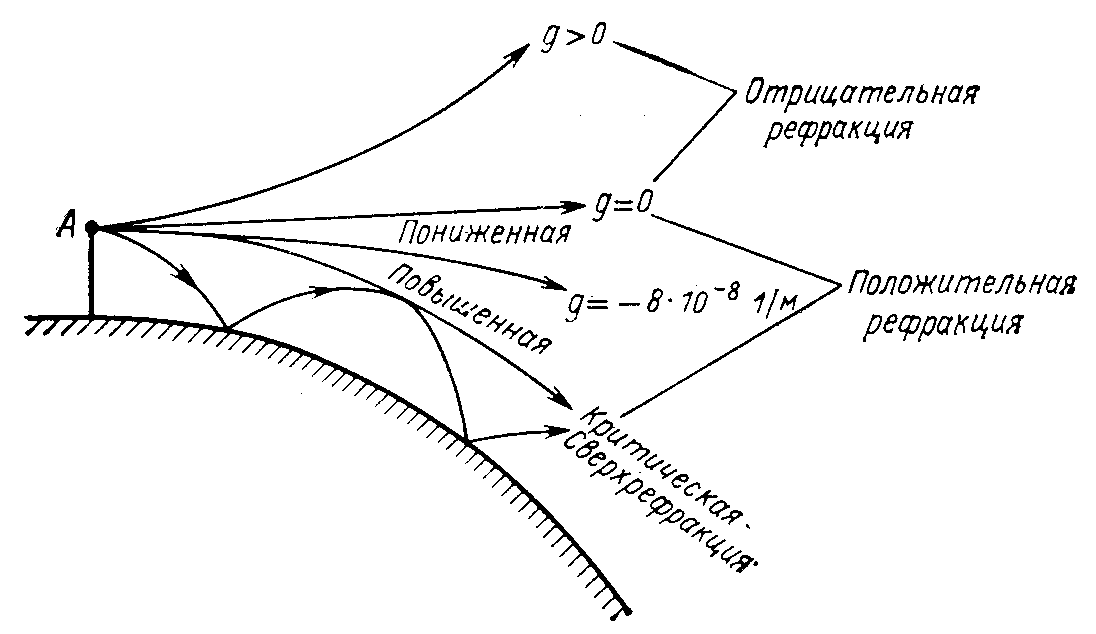
2.7. Виды рефракции

В
зависимости от значений g
и
а_э
различают
следующие виды рефракции радиоволн в
тропосфере (рис. 2.5).

Отрицательная
рефракция
или
субрефракция,
которая
наблюдается при g>0,
а_э<a,
K_э<1.
Субрефракция появляется при возрастании
влажности воздуха с высотой, причем
наиболее часто осенью или весной во
время утренних приземных туманов. Она
нередко носит местный характер и
отмечается на трассе РРЛ или ее участке,
где имеются низины, и застаивается
холодный воздух.

Положительная
рефракция,
которая
наблюдается при g<0,
а_э>а,
K_э>1.

Рис.
2.5.
Виды рефракции в тропосфере

Частные случаи
положительной рефракции:

1.
Стандартная рефракция при g
= –8∙10^-8
м^–1;
а_э
= 8500 км; K_э
= 4/3. Это наиболее распространенный
случай рефракции, обусловленный средним
состоянием тропосферы. Рефракция,
близкая к стандартной, наблюдается чаще
в дневные часы.

2.
Повышенная рефракция при g
< –8∙10^-8
м^–1;
а_э>
8500 км. Наиболее часто отмечается в
вечерние, ночные и утренние часы летних
месяцев, а иногда в эти же часы весной
или осенью. Причиной возникновения
являются температурные инверсии
(увеличение температуры воздуха с
высотой) и резкое уменьшение влажности
с высотой, связанные с нагреванием и
охлаждением земной поверхности
испарением с почвы, сменой теплых и
холодных воздушных масс и т.д.

3.
Критическая рефракция при g_к
= –2/а
= –31,4∙10^-8
м^–1;
а_э
= ∞, т. е. траектория волны концентрична
земной поверхности. Условия возникновения
те же, что для повышенной рефракции.

4
Сверхрефракция при g
< –31,4∙10^-8
м^–1,
а_э
принимает отрицательные значения.
В этом случае волны преломляются к
поверхности земли, отражаются от нее,
снова преломляются и т.д. Распространение
радиоволн при сверхрефракции называют
волноводным, так как оно происходит в
пределах тропосферного волновода.
Волноводные условия распространения
возникают также при резких изломах
высотного профиля диэлектрической
проницаемости воздуха, вызывающих
сильные отражения радиоволн.

Волноводы могут
появляться в приземном (приводном) и в
приподнятом слоях воздуха. При этом они
обнаруживаются как по всей трассе, так
и на отдельных ее участках. Волноводные
условия распространения возникают
главным образом над теплыми морями,
реже — над сушей, в районах с ровной
подстилающей поверхностью. В южных
морских районах в летние месяцы
тропосферные волноводы могут
наблюдаться до 30-50% времени, в сухопутных
— до 10 %.

Несмотря
на значительное увеличение дальности
связи при волноводном распространении
(сотни километров), это явление не может
быть использовано
для
практических целей из-за малой вероятности
появления волноводов. Его следует
рассматривать как источник дополнительных
замираний или помех на интервалах
РРЛ, работающих на одинаковых или близких
частотах.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Эквивалентный радиус из антенны проводника определяется следующим образом:

$r_ {e} = exp left {{1 over L ^ {2}} oint _ { ell} oint _ { ell} ln vert { boldsymbol {x}} - { boldsymbol {y}} vert ; dx ; dy right }$

где обозначает дирижер окружность , длина окружности, и являются векторами фиксирующих точек вдоль окружности, а также и дифференциалы сегменты вдоль нее. Эквивалентный радиус позволяет использовать аналитические формулы или расчетные или экспериментальные данные, полученные для антенн, построенных из небольших проводников с однородным круглым поперечным сечением, которые можно применять при анализе антенн, построенных из небольших проводников с однородными некруглыми поперечными сечениями. Здесь «малый» означает, что наибольший размер поперечного сечения намного меньше длины волны .

Формулы

В следующей таблице перечислены эквивалентные радиусы для различных поперечных сечений проводников, полученные при условии, что 1) все размеры намного меньше , 2) для поперечных сечений, состоящих из нескольких проводников, расстояния между проводниками намного больше, чем любой отдельный размер проводника. . Формулы для квадратного и треугольного сечений следуют из численной оценки двойного интеграла. Все остальные формулы точны.

Поперечное сечение	Описание	Эквивалентный радиус
	Два одинаковых круглых проводника
	Два круглых проводника с разным радиусом	$exp left {{r_ {1} ^ {2} ln r_ {1} + r_ {2} ^ {2} ln r_ {2} + 2r_ {1} r_ {2} ln S over (г_ {1} + г_ {2}) ^ {2}} right }$
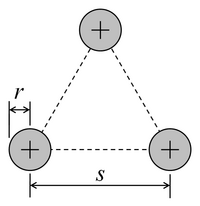
	Идентичные круглые проводники, расположенные в треугольнике	$left (rs ^ {2} right) ^ {{1/3}}$
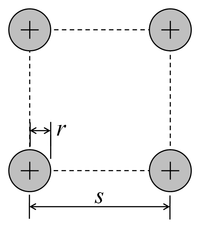
	Идентичные круглые проводники, расположенные в квадрате	$left ({ sqrt {2}} , rs ^ {3} right) ^ {{1/4}}$
	Идентичные круглые проводники, расположенные в пятиугольнике	$left (2.62 , rs ^ {4} right) ^ {{1/5}}$
	Идентичные круглые проводники, расположенные в шестиугольнике	$left (6 , rs ^ {5} right) ^ {{1/6}}$
	Идентичные круглые проводники, равномерно расположенные по кругу	${ displaystyle left (NrR ^ {N-1} right) ^ {1 / N}}$
	Плоский бесконечно тонкий проводник	$displaystyle {We ^ {{- 3/2}} приблизительно 0,22 , Вт}$
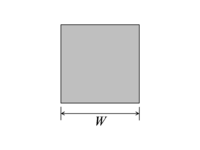
	Квадратный проводник
	Равносторонний треугольник проводник

Вывод

Эквивалентный радиус получается путем приравнивания среднего магнитного векторного потенциала на поверхности проводника произвольного поперечного сечения к потенциалу на поверхности цилиндра.

Предположим, что размеры поперечного сечения проводника малы по сравнению с длиной волны, ток течет только в осевом направлении вдоль проводника, распределение тока медленно изменяется по длине проводника, а ток примерно равномерно распределяется по его окружности (из-за скин-эффекта ). Кроме того, только ток в окрестности любой точки на проводе значительно влияет на потенциал в этой точке. Зависимость от времени игнорируется, так как она может быть включена путем умножения распределения тока на изменяющуюся во времени синусоиду. Эти условия подразумевают, что существует квазистатическое состояние и что геометрия, по сути, представляет собой один из бесконечно длинного проводника с постоянной плотностью поверхностного тока (ток на площадь), тем самым сводя трехмерную задачу к двумерной. Также подразумевается, что вектор магнитного потенциала параллелен оси проводника.

Сначала рассмотрим потенциал в фиксированной точке на окружности произвольного поперечного сечения. С окружностью, разделенной на дифференциальные сегменты , распределение тока может быть аппроксимировано размещением вертикальной линии тока внутри каждого сегмента, каждый с линейной плотностью (ток на длину). Хорошо известно, что потенциал такого линейного тока равен , где — постоянная проницаемости. Потенциал при равен сумме потенциалов для всех полосок, которая равна
${ displaystyle scriptstyle {- ( mu _ {0} Qdx / 2 pi) ln vert { boldsymbol {x}} - { boldsymbol {y}} vert}}$ ${ displaystyle scriptstyle { mu _ {0}}}$

${ displaystyle A ({ boldsymbol {y}}) = - { mu _ {0} Q over 2 pi} oint _ { ell} ln vert { boldsymbol {x}} - { полужирный символ {y}} vert ; dx.}$

Тогда средний потенциал равен

${ displaystyle { bar {A}} = {1 over L} oint _ { ell} A ({ boldsymbol {y}}) ; dy , = - { mu _ {0} Q более 2 pi L} oint _ { ell} oint _ { ell} ln vert { boldsymbol {x}} - { boldsymbol {y}} vert ; dx ; dy.}$

Теперь рассмотрим случай цилиндра с той же линейной плотностью тока, что и проводник произвольного сечения. Также хорошо известно, что потенциал в любой точке на его поверхности, который также равен ее среднему потенциалу, равен

${ displaystyle A_ {c} = - { mu _ {0} QL over 2 pi} ln left (r_ {e} right).}$

Приравнивание и урожайность
${ displaystyle scriptstyle {A_ {c}}}$

$ln left (r_ {e} right) = {1 over L ^ {2}} oint _ { ell} oint _ { ell} ln vert { boldsymbol {x}} - { boldsymbol {y}} vert ; dx ; dy.$

Возведение в степень с обеих сторон приводит к формуле эквивалентного радиуса.

Формула эквивалентного радиуса дает согласованные результаты. Если размеры поперечного сечения проводника масштабируются на коэффициент , эквивалентный радиус масштабируется на . Кроме того, эквивалентный радиус цилиндрического проводника равен радиусу проводника.

Рекомендации

Источник

ЭКВИВАЛЕНТНЫЙ РАДИУС ТЕЛА [c.172]

Величина (эквивалентный радиус) находится из условия равенства объемов рассматриваемого и эквивалентного тел. [c.172]

Тела первого класса. Приравняв объем рассматриваемого и эквивалентного тел, найдем эквивалентный радиус для тел первого класса (стенки) [c.172]

Тела второго класса. Аналогичным образом находим эквивалентный радиус для тел второго класса (цилиндры и призмы) [c.173]

Здесь для тел первО ГО класса (станки) i=l, для тел второго класса г== /2 и для тел третьего класса = /з величина Xq есть эквивалентный радиус рассматриваемого тела. [c.175]

Нужно, однако, помнить, что введение эквивалентного радиуса и эквивалентного давления чисто условно, так как природа сил взаимодействия между лучистой энергией и телом несколько отлична от природы сил взаимодействия двух твердых тел в процессе соприкосновения. [c.113]

Приближение, связанное с предположением о малости вторичного течения, позволяет свести решение пространственной задачи к решению набора двумерных задач около тела с некоторым эквивалентным радиусом. Обычно в этом случае используется система координат, связанная с линиями тока внешнего течения. Вдоль линий тока задача решается путем использования теории пограничного слоя для двумерных течений. Профили скорости задаются в параметрическом виде [c.149]

В системе координат, связанной с линиями тока внешнего течения, часто используют осесимметрическую аналогию. Уравнения трехмерного пограничного слоя сводятся к виду, напоминающему осесимметрический случай. Вдоль каждой линии тока решается двумерная задача, как около тела с некоторым эквивалентным радиусом. В этом случае для неизвестных управляющих функций получается система обыкновенных дифференциальных уравнений. Решение в первом приближении получается в квадратурах. В случае локально-автомодельного приближения относительно неизвестных управляющих функций получается алгебраическая система уравнений. [c.153]

Мы определили выражения для эквивалентного радиуса области контакта с = (аЬ) > , максимального контактного давления Ро и сближения тел б через эквивалентный радиус Ее — = (Я (см. выражения (4.30) — (4.32)). Сравнение с соот- [c.114]

В нагруженном состоянии отношение полуосей равно а/Ь 3.18 по данным рис. 4.4 и а/Ь л 3.25 по выражению (4.33). Из рис. 4.4 находим также Fl 2 0.95 и 1.08. Теперь эквивалентный радиус области контакта с = аЬ) сближение тел б и максимальное контактное давление ро можно определить из выражений (4.30) — (4.32) соответственно. [c.115]

Сведение проблемы к эквивалентной задаче для одного тела. Рассмотрим консервативную систему, состоящую из двух точек с массами гп и т . Единственными силами, действующими на эти точки, мы будем считать силы, обусловленные потенциалом взаимодействия V, относительно которого мы будем предполагать, что он является функцией вектора Г — Г2, относительной скорости Г1 — Г2 и производных более высокого порядка от fi — Г2. Рассматриваемая система имеет шесть степеней свободы и, следовательно, характеризуется шестью независимыми обобщенными координатами. В качестве таких координат мы выберем три составляющих радиуса-вектора R, идущего в центр масс системы, и три составляющих вектора г = Г2 — Тогда лагранжиан этой системы будет иметь вид [c.72]

Ниже представлены результаты численных расчетов для следующих двадцати вариантов (табл. 8-1), объединенных в четыре группы. Переход от одного варианта к другому в каждой группе соответствует уменьшению коэффициента теплообмена вдвое. Это эквивалентно согласно теории теплообмена в ламинарном пограничном слое изменению радиуса кривизны тела R в группе более чем в 250 раз. [c.211]

Лучшее согласование экспериментальных данных с теоретическими дает метод эквивалентной задачи теории теплопроводности [3], если, следуя эксперименту, для каждого сечения потока задавать начальное распределение температуры для эквивалентной задачи в виде кольца постоянной температуры на бесконечной плоскости таким образом, чтобы его площадь оставалась равной площади сечения потока на срезе сопла, а средний радиус был равен среднему радиусу кольцевой струи в рассматриваемом сечении. Последний определяется из эксперимента как радиус окружности максимальных значений плотности потока импульса или избыточного теплосодержания. При таком расчете получается плавное изменение всех параметров вдоль оси потока, начиная от его среза. Заметим, что метод линеаризации уравнений движения, предложенный Г. Рейхардтом, был также, применен к расчету потока с градиентами статического давления (основной участок следа за плохо обтекаемым телом) [2]. [c.198]

Результаты, представленные на рис. 2.4,а, показывают, что зависимости нагрузки Р от расстояния D являются немонотонными и имеют точку минимума. На величину этого минимума наиболее сильно оказывает влияние параметр ст, с ростом которого абсолютные значения минимальных нагрузок возрастают. Увеличение параметра а, связанное либо с увеличением поверхностного натяжения, либо с уменьшением эквивалентного модуля упругости взаимодействующих тел, приводит к росту абсолютного значения ро давления в жидкости (см. рис. 2.4,5) и радиуса 6 области занятой жидкостью (см. рис. 2.4,е). При увеличении объёма жидкости в мениске (увеличение параметра v) наблюдаются увеличение радиуса 6 и уменьшение давления Ро жидкости в мениске, особенно в случае, когда сохраняется контакт поверхностей. На основании полученных результатов [c.93]

Займемся теперь определением момента инерции эквивалентного тела. Интеграл в формуле (54) нам придется брать только по радиусу ОА в направлении от А к О, так как на дуге АС имеем = 0. Вследствие того что на радиусе ОА функция F равна Ф, [c.240]

Мы ниже всюду будем считать, что вне некоторой сферы конечного радиуса i/(r) = 0, так что эквивалентное тело занимает конечный объем. По-видимому, аппарат может быть обобщен и на потенциалы, асимптотически стремящиеся к нулю при г- оо. [c.68]

Эти смещения будут вызываться системой сил, приложенных к внутренней стороне полусферы малого радиуса г, описанной из начала координат. Эта система сил статически эквивалентна одной равнодействующей силе Р, приложенной в начале и направленной по положительной оси г вся же остальная граница упругого тела будет свободна от каких бы то ни было приложенных сил. [c.157]

Это решение удовлетворяет уравнениям равновесия (14) и условиям на поверхности (3) во всех точках тела, кроме точки приложения силы, в которой напряжения и перемещения становятся бесконечно большими. Затруднения, возникающие в этом решении, обладающем особой точкой, преодолеваются при помощи принципа Сен-Венана. Предполагается, что у начала координат материал вырезан полусферической поверхностью малого радиуса и что сосредоточенная сила Р заменена статически эквивалентными усилиями, распределёнными по этой поверхности. Это условие приводит к уравнению [c.121]

НИИ тока имеют малую геодезическую кривизну. При значениях отношения скорости поперечного течения в пограничном слое к полной местной скорости, равных / 7 0,Зч-0,4, можнс) использовать принцип независимости поперечного течения от продольного. В предположении о малости вторичного течения получаем уравнения движения, аналогичные уравнениям пограничного слоя около осесимметрического тела, из которых находится продольная скорость, и отдельного уравнения для поперечной скорости, которое дает возможность определить эту величину. Параметры трехмер- ного пограничного слоя можно рассчитать, пользуясь этой аналогией, если известен эквивалентный радиус тела который определяется не только геометрией тела, но и параметрами внешнего потока. Для расчета метрического коэффициента используют поле скоростей идеального невязкого потока или распределение давления на поверхности (см. гл. V). Воспользуемся методом последовательных приближений (см. [22]). [c.161]

Для конкретных форм излучающих тел это уравнение можно проинтегрировать. Однако простое решение для бипол получено лишь для газообразного тела полусферической формы [79]. Для расчета излучения тел сложной формы Хоттель предложил ввести полусферу эквивалентного радиуса, излучающую так, что для всех значений [c.231]

Отметим, что величины и д д зависят от расстояния г о. Это связано с тем, что в данном случае мы имеем дело с телом, длина к которого настолько велика, что точка излучения-приема находится в ближней зоне, определяемой неравенством г о При этом на длине отрезка Н укладываются несколько зон Френеля. Эффективно участвует в формировании процесса отражения лишь первая зона, а остальные компенсируют друг друга. При увеличении расстояния до цилиндра размер первой зоны увеличивается и в процесс образования отраженной волны вовлекается все бшьшая часть цилиндра. Этот процесс происходит до тех пор, пока выполняется приведенное нфавенство. Для тел, размеры которых малы по сравнению с расстоянием до объекта (точнее, если Го > >й /Х), поперечник рассеяния и эквивалентный радиус не зависят от расстояния. [c.198]

Для решения задачи воспользуемся известным из вузовских курсов физики результатом, а именно на любое точечное тело массой т, находящееся внутри однородной гравитирующей сферы радиусом R (рис. 6), действуют лишь часгицы, расположенные в сфере радиусом г, где г — расстояние от центра сферы до пробного тела массой т. Действие этих частиц эквивалентно тому, что вся масса сферы радиусом г сосредоточена в ее центре [42]. При этом на пробное тело т действует сила притяжения [c.59]

При построении аналитических моделей, описывающих удар, следует иметь в виду, что использование концепции эквивалентного анизотропного материала является спорным, если требуется определить напряжения в окрестности области контакта. Если тело из композиционного материала заменяется другим телом с выпуклой поверхностью, то при убывании давления площадь контакта стремится к нулю, и при малых силах размеры области контакта оказываются соизмеримыми с размерами волокон или толщиной слоев. По мере того как область контакта захватывает отдельные волокна, следует ожидать периодических изменений диаграммы деформирования. Этим можно объяснить волнообразный характер кривой, определяющей деформирование бороалю-миния с содержанием волокон 50% (рис. 25). Периодические пологие участки соответствуют радиусам площадки контакта, отличающимся на величину, равную расстоянию между волокнами ( -0,1 мм). Необходимы дальнейшие экспериментальные исследования в этом направлении. [c.320]

Для газовых тел, имеющих форму шара, бесконечного цилиндра, плоского слоя, dv,dF = dv,F и, следовательно, av,dF = av,F- Поэтому для определения пропускагель-ной или поглощательной способности такого газового тела по отношению к полному излучению поверхности ограждения F можно ограничиться определением dv,dF и av,dF для какого-нибудь элемента dF поверхности f. Газовое тело, с точки зрения его пропускательной или поглощательной способности по отношению к полному излучению элемента dF поверхности ограждения, может быть заменено эквивалентным полусферическим газовым телом радиуса R=Saii имеющим такие же пропускатель-ную и поглощательную способности по отношению к полному излучению этого же элемента поверхности dF, помещенному в центре основания полусферы (рис. 15-7). 248 [c.248]

Различие закономерностей лучистого теплообмена, теплопроводности и конвекции, участвующих в переносе тепла в экранной изоляции, сильно осложняет решение задачи даже в тех случаях, когда все три процесса протекают независимо друг от друга. После введения К. Хенки понятия эквивалентного коэффициента теплопроводности воздуха появилась возможность производить расчеты теплопередачи через воздушные прослойки, пользуясь простыми формулами теплопередачи через твердые тела. Этот эквивалентный коэффициент теплопроводности, объединяющий все три вида теплопередачи в одну расчетную величину, зависит от толщины воздушной прослойки, радиуса ее кривизны, характера ограничивающих ее поверхностей и т. д. [c.11]

Во-вторых, понятие о радиусе корреляции в [102] не только ошибочно трактуется, но и неправильно используется. Можно было бы повторить все выкладки, предшествующие получению выражения (3.76), рассматривая не распространение возмущения по фрактальному кластеру скелета дисперсного тела, а эквивалентную задачу [52] о вытеснении жидкости из насыщенного норового пространства, также образующего фрактальный кластер. В результате мы бы получили точно такое же выражение. [c.90]

Предположим, что характерный размер макротрещины (радиус, длина и т.п.) велик по сравнению с искомой длиной 2Lq поперечных цилиндрических трещин сдвига, образующихся при пересечении нитей макротрещиной. Будем считать на основании этого допущения, что отличное от нуля распределение касательного напряжения Тгг на продолжении трещин сдвига вдоль боковых поверхностей нитей целиком лежит в области действия асимптотики фронта макротрещины. Следовательно, вытаскивающая сила, действующая на образованную нить на фронте трещины, может быть найдена из усредненной асимптотики напряжения Oz (для эквивалентного орто-тропного тела) вблизи фронта трещины при л = О (см. рис. 37). Используя известную асимптотику на фронте трещины в анизотропном теле, можно найти [1] [c.87]

Физическую причину различия предельных значений и С/ легко понять, учитывая, что это различие связано с коэффициентом Пуассона, который определяет сокращение поперечных размеров стержня при его удлинении. В случае тонкого стержня изменение его поперечных размеров при продольных деформациях не встречает сопротивления со стороны внешней среды, что эквивалентно меньшей эффективной жесткости по сравнению с безграничным телом при 0. В свою очередь, наличие поперечных пульсаций при распространении продольных волн в тонком стержне означает зависимость его поперечных размеров, т. е. площади 5, от координаты д , что не учитывалось при выводе уравнения (Х.74). Учет этого обстоятельства, выполненный Рэлеем (11 для круглого стержня радиусом Н, приводит к убыванию скорости с увеличением частоты при / < А. Физическая причина этого явления состоит в том, что возбуждение радиальных колебаний при продольных деформациях стержня приводит к большей кинетической энергии колеблющихся частиц по сравнению с чисто продольными колебаниями, что эквивалентно большей колеблющейся массе, т. е. меньшей эффективной жесткости для продольных волн. Когда длина волны Л становится соизмеримой с диаметром стержня, поперечный эф4 ект вызывает резонансные радиальные колебания. В резонансной области наблюдается аномальная дисперсия скорость продольных волн падает до нуля, а затем при дальнейшем увеличении частоты быстро возвращается из бесконечности, устремляясь к новому, высокочастотному предельному значению с (оо) = с,, определяемому формулой (Х.76). Общая картина геометрической дисперсии качественно изображена на рис. 69, который хорошо согласуется с экспериментальными данными [12]. Вся область существенной дисперсии на этой картине располагается в небольшом диапазоне частот, соответствующем изменению длины волны Л на (30 40) 0 относительно радиуса стержня. Однако, как показывает опыт, при точных измерениях скорости распространения ультразвуковых волн в стержневидных образцах геометрическая дисперсия ощущается даже тогда, когда поперечные размеры стержня превышают длину ультразвуковой волны в десятки и сотни раз [78]. [c.235]

Так как момент инерции куба есть то момент инерции эквивалентного те.аа составляет, только 0,1565 момента инерции эюидкой массы. Самому эквивалентному телу в этом случае можно дать форму шарика, радиус которого равен 0,2554 . [c.214]

Задача Ге.1ьнгольца о колебаниях около неподвижной оси шара, наполненного трущеюся жидкостью. Для первого примера рассмотрим задачу Гельмгольца о колебании около неподвижной оси тела, содерисащего в своей шаровой полости радиуса а трущуюся жидкость и находящегося под действием пары, момент которой пропорционален угловому перемещению тела, считая от положения его равновесия. Примем в формуле (5) ось Ох за ось вращения тела и определим А, присоединив к твердому телу эквивалентное тело, которое в нашем с.пучае будет материальною точкою, равною по массе жидкости и помещенною в центре шара. [c.281]

Н. Л, Крашенинникова (1955) рассмотрела задачу о расширении в покоящемся газе поршня с радиусом В, зависящим от времени по степенному закону В f + . Решение этой задачи автомодель-но, если пренебречь начальным давлением газа. Крашенинникова провела исследование задачи для нескольких комбинаций тг и V (V = 1, 2, 3 для течений с плоскими, цилиндрическими и сферическими волнами) и установила, что решение с ударной волной, отделяющей покоящийся газ от области возмущенного поршнем движения, существует не для всех комбинаций этих величин. Л. Г. Велеско, Г. Л. Гродзовский и Н, Л. Крашенинникова (1956) провели систематические расчеты автомодельных течений, возникающих при расширении цилиндрического поршня для значений ге от О до —0,35. Этим течениям эквивалентны симметричные течения около тел вращения степенной формы при числе Маха М = оо. [c.186]

Здесь е — элементарный заряд, 2 — порядковый номер ядра, Лд, радиус ядра в основном и возбужденном состояниях (точнее радиус эквивалентной равномерно заряженной сферы). Изомерные сдвиги подробно изучались для соединений железа и олова (рисунки Н, 8). Анализ результатов приводит к заключению, что радиус ядра Ге в возбужденном состоянии с энергией 14,4 кэе примерно на 0,1% меньше радиуса основного состояния. Для 8и 1 радиус возбужденного состояния с энергией 24 кэе примерно на 0,01% больше радиуса основного состояния. Исследование изомерных сдвигов дает также сведения о плотности -элек-тронов на ядре, важные для химии и физики твердого тела. [c.185]

Последнее решено приближенно методом ортогональных многочленов (I, 4, 2°). Как частный случай в этой же работе рассмотрена осесимметричная задача Герца с учетом поверхностной структуры контактирз -мых тел, что эквивалентно решению уравнения (2.29) при /г=0, и, в частности, вдавливание штампа в виде параболоида вращения в упругое комбинированное основание. Для последней задачи приведена таблица, облегчающая нахождение радиуса площадки контакта. [c.294]

Источник

Изобретение относится к защите подземных сооружений от коррозии и может быть использовано при определении дефектов в изоляционном покрытии подземных сооружений, например подземных трубопроводов. Все измерения производятся при включенной катодной защите. Измеряют напряжение между двумя электродами сравнения, потенциал «подземное сооружение-земля» с омической составляющей и поляризационный потенциал «подземное сооружение-земля». Дополнительно синхронно измеряют омическую составляющую потенциала «подземное сооружение-земля», сравнивают измеренное значение омической составляющей потенциала «подземное сооружение-земля» с разностью между потенциалом «подземное сооружение-земля» с омической составляющей и поляризационным потенциалом «подземное сооружение-земля», выбирают значение омической составляющей потенциала «подземное сооружение-земля», имеющее минимальное отклонение от сравниваемых величин, после чего определяют размеры радиуса эквивалентного дефекта в изоляционном покрытии подземного сооружения. Обеспечивает повышение точности определения эквивалентного радиуса выявленного дефекта в изоляционном покрытии подземного сооружения, например трубопровода. 2 с.п. ф-лы, 2 ил.

Изобретение относится к области защиты подземных сооружений от коррозии и может быть использовано при определении наличия и характера дефектов в изоляционном покрытии подземных сооружений, например подземных трубопроводов.

Для оценки новизны и изобретательского уровня первого из двух заявленных объектов изобретения рассмотрим ряд известных технических средств аналогичного назначения.

Известны способы определения дефектов в изоляционном покрытии трубопровода, основанные на измерении параметров электрического поля, заданного высокочастотным генератором при помощи приемника с направленной антенной (см. Руководство по эксплуатации средств противокоррозионной защиты подземных трубопроводов. М.: Мингазпром, ВНИИГАЗ, 1986, стр. 39-62).

Эти способы позволяют определить наличие дефекта в изоляционном покрытии подземного сооружения, но не позволяют определить его геометрические размеры, что является весьма важной информацией для определения характера аварийной ситуации, ее возможного развития и методов ее устранения.

Наиболее близким к заявленному способу является известный способ определения дефектов в изоляционном покрытии подземных сооружений, заключающийся в том, что измеряют напряжение между двумя электродами сравнения, потенциал «подземное сооружение-земля» с омической составляющей и поляризационный потенциал «подземное сооружение-земля» (см. В. Бекман. Катодная защита. — М: Металлургия, 1992, стр. 122, рис. 81).

Теоретическая основа данного способа состоит в том, что потенциал «подземное сооружение-земля» состоит из трех составляющих U_ein=U_aus+U_ir, где V_ein — потенциал «подземное сооружение-земля» с омической составляющей, В; U_aus — поляризационный потенциал «подземное сооружение-земля», В; U_ir — омическая составляющая потенциала «подземное сооружение-земля», В.

Определение эквивалентного радиуса дефекта в изоляционном покрытии подземного сооружения производится по формуле Ro = 1,74U/(Uein-Uaus), где R₀ — эквивалентный радиус дефекта в изоляционном покрытии, м; U — разность потенциала между двумя медно-сульфатными электродами сравнения, В.

По наибольшему количеству сходных признаков и достигаемому при использовании результату данное техническое решение выбрано в качестве прототипа заявленного способа.

Серьезной технической проблемой при реализации данного способа является невозможность синхронного измерения требуемых для расчета эквивалентного радиуса дефекта величин U, U_ein и U_aus, так как U_ein измеряется при включенной катодной защите подземного сооружения, а U_aus — при отключенной катодной защите, в момент, когда U не измеряется. Другим недостатком этого способа является невозможность проверки точности измерений U_ein и U_aus.

Для оценки новизны и изобретательского уровня второго заявленного объекта изобретения рассмотрим известные технические средства аналогичного назначения.

Наиболее близким к заявленному устройству по своей технической сущности является устройство, содержащее измерительные каналы, входы одного из которых соединены с двумя электродами сравнения, а входы другого соединены с электродом сравнения и контрольным проводником от подземного трубопровода (см. В.Бекман. Катодная защита. — М.: Металлургия, 992, стр. 122, рис. 81).

По наибольшему количеству сходных признаков и достигаемому при использовании результату данное техническое решение выбрано в качестве прототипа заявленного устройства.

Недостатками прототипа, не позволяющими достичь поставленной нами цели, является низкая точность определения эквивалентного радиуса дефекта в изоляционном покрытии трубопровода, обусловленная вышеуказанными недостатками реализуемого способа измерений.

Задачей изобретения является повышение точности определения эквивалентного радиуса дефекта в изоляционном покрытии подземного сооружения.

Сущность первого самостоятельного объекта заявляемого изобретения выражается в следующей совокупности существенных признаков, достаточной для достижения указанного выше технического результата.

Согласно изобретению способ определения наличия и эквивалентного радиуса дефекта в изоляционном покрытии подземного сооружения, заключающийся в том, что измеряют напряжение между двумя электродами сравнения, потенциал «подземное сооружение-земля» с омической составляющей и поляризационный потенциал «подземное сооружение-земля», характеризуется тем, что дополнительно синхронно измеряют омическую составляющую потенциала «подземное сооружение-земля», сравнивают измеренное значение омической составляющей потенциала «подземное сооружение-земля» с разностью между потенциалом «подземное сооружение-земля» с омической составляющей и поляризационным потенциалом «подземное сооружение-земля», выбирают значение омической составляющей потенциала «подземное сооружение-земля», имеющее минимальное отклонение от сравниваемых величин, после чего на основе окончательно выбранного значения омической составляющей потенциала «подземное сооружение-земля» определяют размеры радиуса эквивалентного дефекта в изоляционном покрытии подземного сооружения.

В этом заключается совокупность существенных признаков первого самостоятельного объекта заявленного изобретения, обеспечивающая получение технического результата во всех случаях, на которые распространяется испрашиваемый объем правовой охраны.

Сущность второго самостоятельного объекта заявляемого изобретения выражается в следующей совокупности существенных признаков, достаточной для достижения указанного выше технического результата.

Согласно изобретению устройство для определения наличия и эквивалентного радиуса дефекта в изоляционном покрытии подземного сооружения, содержащее измерительные каналы для синхронного измерения электрических параметров, входы одного из которых соединены с двумя электродами сравнения, а входы другого соединены с электродом сравнения и контрольным проводником от подземного сооружения, характеризуется тем, что каждый измерительный канал снабжен интегратором, ключом, двумя синхронными детекторами, генератором тактовых импульсов, сумматором, двумя преобразователями напряжение — частота, двумя элементами оптической развязки, при этом устройство дополнительно снабжено датчиком потенциала, выходным устройством для контроля и передачи информации, включающим коммутатор, измерительный прибор, запоминающее устройство и разъем для соединения устройства с внешним компьютером, при этом входы интегратора, ключа и первого синхронного детектора первого канала соединены с первым электродом сравнения, вход второго синхронного детектора первого канала соединен со вторым электродом сравнения, причем другие входы синхронных детекторов в каждом канале соединены с выходом генератора тактовых импульсов, другой выход которого соединен со входом ключа, а выходы синхронных детекторов соединены со входами сумматора, выход которого соединен со входом первого преобразователя напряжение-частота, один вход сумматора соединен с входом второго преобразователя напряжение-частота, выходы которых соединены с элементами оптической развязки, кроме того первый вход интегратора второго канала соединен с подземным сооружением, второй вход интегратора второго канала соединен с выходом ключа, датчиком потенциала и входом первого синхронного детектора второго канала, вход второго синхронного детектора второго канала соединен со вторым электродом сравнения, а вход первого синхронного детектора третьего канала соединен с подземным сооружением, вход второго синхронного детектора третьего канала соединен со вторым электродом сравнения, один из входов и выход сумматоров всех измерительных каналов соединены со входами коммутатора выходного устройства, выход которого соединен с измерительным прибором, выходы элементов оптической развязки измерительных каналов соединены с входами запоминающего устройства, выход которого снабжен разъемом для связи с внешним компьютером.

Заявленное техническое решение является новым, так как характеризуется наличием новой совокупности признаков, отсутствующей во всех известных нам объектах техники аналогичного назначения.

Непосредственный технический результат, который может быть получен при реализации заявленной совокупности признаков, заключается в том, что все измерения проводятся при включенной катодной защите подземного сооружения, в момент, когда напряжение между датчиком потенциала и подземным сооружением равно нулю, что позволяет более точно измерить составляющие потенциала «подземное сооружение-земля» и максимально точно определить эквивалентный радиус выявленного дефекта.

Получение упомянутого технического результата обеспечивает появление у объекта изобретения в целом ряда новых полезных свойств, а именно повышение точности определения эквивалентного радиуса выявленного дефекта в изоляционном покрытии подземного сооружения.

Указанное позволяет признать заявленное техническое решение соответствующим критерию «изобретательский уровень».

Сущность изобретения поясняется чертежом, где на фиг. 1 представлена блок-схема заявленного устройства, на фиг. 2 представлены диаграммы, поясняющие характер синхронно измеряемых устройством напряжений.

Устройство 1 содержит измерительные каналы 2, 3, 4 для синхронного измерения электрических параметров, электроды сравнения Э1, Э2, датчик потенциала D, контрольный проводник от размещенного в земле 3 подземного сооружения, например трубопровода T, каждый канал 2, 3, 4 содержит интегратор 5, ключ 6, два синхронных детектора 7, 8, генератор тактовых импульсов 9, сумматор 10, два преобразователя напряжение-частота 11, 12, два элемента оптической развязки 13, 14, выходное устройство для контроля и передачи информации 15, содержащее коммутатор 16, измерительный прибор 17, запоминающее устройство 18, и разъем 19 для соединения устройства с внешним компьютером. Входы интегратора 5, ключа 6, синхронного детектора 7 первого канала 2 соединены с первым электродом сравнения Э1, другие входы синхронных детекторов 7, 8 в каждом канале соединены с выходом генератора тактовых импульсов 9, другой выход которого соединен с входом ключа 6, а выходы синхронных детекторов 7, 8 соединены с входами сумматора 10, выход которого соединен с входом первого преобразователя напряжение-частота 11, один вход сумматора 10 соединен с входом второго преобразователя напряжение-частота 12, выходы которых соединены с элементами оптической развязки 13, 14. Первый вход интегратора 5 второго канала 3 соединен с подземным сооружением T, второй вход интегратора 5 второго канала 3 соединен с выходом ключа 6, датчиком потенциала D и входом первого синхронного детектора 7 второго канала 3, вход второго синхронного детектора 8 второго канала 3 соединен со вторым электродом сравнения Э2, а вход первого синхронного детектора 7 третьего канала 4 соединен с подземным сооружением T, вход второго синхронного детектора 8 третьего канала 4 соединен со вторым электродом сравнения Э2, один из входов и выход сумматоров 10 всех измерительных каналов соединены со входами коммутатора 16 выходного устройства 15, выход которого соединен с измерительным прибором 17, выходы элементов оптической развязки 13, 14 всех измерительных каналов соединены с входами запоминающего устройства 18, выход которого снабжен разъемом 19 для связи с внешним компьютером.

Устройство, реализующее заявленный способ, работает следующим образом. Все измерения производятся при включенной катодной защите, при измерениях каналом 2 устройства 1 потенциала U между электродами сравнения Э1, Э2, напряжение от них поступает на входы синхронных детекторов 7, 8, с выхода которых сигналы поступают на вход сумматора 10, с выхода которого напряжение U поступает на вход преобразователя напряжение-частота, с выхода которого сигнал поступает на вход элемента оптической развязки 13, с выхода которого сигнал поступает на входы запоминающего устройства 18.

При измерениях каналом 3 устройства 1 поляризационного потенциала «подземное сооружение-земля» U_aus и омической составляющей «потенциала подземное сооружение-земля» U_ir, напряжение от датчика потенциала D поступает на вход синхронного детектора 7 и инвертирующий вход интегратора 5, на неинвертирующий вход которого поступает напряжение от трубопровода T, в результате на выходе интегратора 5 устанавливается такое напряжение, при котором напряжение между датчиком потенциала D и трубопроводом T равно нулю. При этом датчик потенциала D под действием тока катодной защиты поляризуется, генератор тактовых импульсов 9 управляет работой ключа 6 и работой двух синхронных детекторов 7, 8, при этом, когда ключ 6 закрыт, синхронные детекторы 7, 8 открыты, в это время происходит измерение напряжения между датчиком потенциала D и электродом сравнения Э2, напряжение с выхода синхронных детекторов 7, 8 поступает на входы сумматора 10, на один из входов поступает напряжение, равное омической составляющей потенциала «подземное сооружение-земля» U_ir, а на выход — поляризационный потенциал «подземное сооружение-земля» U_aus. Эти напряжения поступают на входы преобразователей напряжение-частота 11, 12, с выхода которых сигналы поступают на входы элементов оптической развязки 13, 14, с выхода которых сигналы поступают на входы запоминающего устройства 18.

При измерениях каналом 4 устройства 1 потенциала «подземное сооружение-земля» с омической составляющей U_ein, напряжение от электрода сравнения Э2 поступает на вход синхронного детектора 7, напряжение от трубопровода T поступает на вход синхронного детектора 8, с выходов синхронных детекторов 7, 8 напряжение поступает на вход сумматора 10, с выхода которого поступает на вход преобразователя напряжение-частота, с выхода которого сигнал поступает на вход элемента оптической развязки 13, с выхода которого сигнал поступает на вход запоминающего устройства 18.

Диаграммы, поясняющие изменение синхронно измеряемых устройством напряжений, показывают, что U_ir = U_ein-U_aus. В этом случае омическая составляющая потенциала «подземное сооружение-земля» U_ir контролируется по формуле U_ir = U_ein-U_aus, а расчет эквивалентного радиуса дефекта в изоляционном покрытии трубопровода производится по формуле R₀ = 1,74 U/(U_ein-U_aus).

Все измеренные величины контролируются при помощи коммутатора 16 выходного устройства 15 и измерительным прибором 17. Расчет эквивалентного радиуса дефекта в изоляционном покрытии производится при помощи внешнего компьютера, присоединенного к разъему 19.

Возможность промышленного применения заявленного технического решения подтверждается успешными испытаниями опытного образца заявленного устройства.

Использование заявленного решения по сравнению со всеми известными средствами аналогичного назначения обеспечивает существенное повышение точности определения эквивалентного радиуса выявленного дефекта в изоляционном покрытии подземного сооружения.

Формула изобретения

1. Способ определения наличия и геометрических размеров дефектов в изоляционном покрытии подземных сооружений, заключающийся в том, что измеряют напряжение между двумя электродами сравнения, потенциал «подземное сооружение-земля» с омической составляющей и поляризационный потенциал «подземное сооружение-земля», отличающийся тем, что дополнительно синхронно измеряют омическую составляющую потенциала «подземное сооружение-земля», сравнивают измеренное значение омической составляющей потенциала «подземное сооружение-земля» с разностью между потенциалом «подземное сооружение-земля» с омической составляющей и поляризационным потенциалом «подземное сооружение-земля», выбирают значение омической составляющей потенциала «подземное сооружение-земля», имеющее минимальное отклонение от сравниваемых величин, после чего на основе окончательно выбранного значения омической составляющей потенциала «подземное сооружение-земля» определяют размеры радиуса эквивалентного дефекта в изоляционном покрытии подземного сооружения.

2. Устройство для определения наличия и геометрических размеров дефектов в изоляционном покрытии подземных сооружений, содержащее измерительные каналы для синхронного измерения электрических параметров, входы одного из которых соединены с двумя электродами сравнения, а входы другого соединены с электродом сравнения и контрольным проводником от подземного сооружения, отличающееся тем, что каждый измерительный канал снабжен интегратором, ключом, двумя синхронными детекторами, генератором тактовых импульсов, сумматором, двумя преобразователями напряжение — частота, двумя элементами оптической развязки, при этом устройство дополнительно снабжено датчиком потенциала, выходным устройством для контроля и передачи информации, включающим коммутатор, измерительный прибор, запоминающее устройство и разъем для соединения устройства с внешним компьютером, при этом входы интегратора, ключа и первого синхронного детектора первого канала соединены с первым электродом сравнения, вход второго синхронного детектора первого канала соединен со вторым электродом сравнения, причем другие входы синхронных детекторов в каждом канале соединены с выходом генератора тактовых импульсов, другой выход которого соединен со входом ключа, а выходы синхронных детекторов соединены со входами сумматора, выход которого соединен со входом первого преобразователя напряжение — частота, один вход сумматора соединен с входом второго преобразователя напряжение — частота, выходы которых соединены с элементами оптической развязки, кроме того, первый вход интегратора второго канала соединен с подземным сооружением, второй вход интегратора второго канала соединен с выходом ключа, датчиком потенциала и входом первого синхронного детектора второго канала, вход второго синхронного детектора второго канала соединен со вторым электродом сравнения, а вход первого синхронного детектора третьего канала соединен с подземным сооружением, вход второго синхронного детектора третьего канала соединен со вторым электродом сравнения, один из входов и выход сумматоров всех измерительных каналов соединены со входами коммутатора выходного устройства, выход которого соединен с измерительным прибором, выходы элементов оптической развязки измерительных каналов соединены с входами запоминающего устройства, выход которого снабжен разъемом для связи с внешним компьютером.

РИСУНКИ

Рисунок 1, Рисунок 2

Источник

2.7. Виды рефракции

Формулы

Вывод

Рекомендации

Возможно, вам также будет интересно: