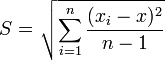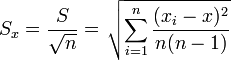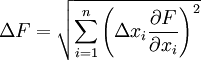Что такое относительная приборная ошибка

18

Ч
а с т ь I

ОБРАБОТКА РЕЗУЛЬТАТОВ
ИЗМЕРЕНИЙ

1.
КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ОШИБОК

Абсолютная
и относительная ошибки

Никакую
физическую величину невозможно измерить
абсолютно точно: как бы тщательно ни
был поставлен опыт, измеренное значение
величины х
будет
отличаться от ее истинного значения Х.
Разница между этими значениями
представляет собой абсолютную
ошибку (или
абсолютную
погрешность^*)
измерения  х :

 х
= х – Х.
(1)

Абсолютная погрешность
является размерной величиной: она
выражается в тех же единицах, что и сама
измеряемая величина (например, абсолютная
погрешность измерения длины выражается
в метрах, силы тока – в амперах и т.д.).
Как следует из выражения (1),  х
может быть как положительной, так и
отрицательной величиной.

Хотя
величина  х
показывает, насколько измеренное
значение отличается от истинного, одной
лишь абсолютной ошибкой нельзя полностью
характеризовать точность проделанного
измерения. Пусть, например, известно,
что абсолютная погрешность измерения
расстояния равна 1 м.
Если измерялось расстояние между
географическими пунктами (порядка
нескольких километров), то точность
такого измерения следует признать
весьма высокой; если же измерялись
размеры помещения (не превышающие
десятка метров), то измерение является
грубым. Для характеристики точности
существует понятие относительной
ошибки
(или относительной
погрешности)
Е,
представляющей собой отношение модуля
абсолютной ошибки к измеряемой величине:

.
(2)

Очевидно, что
относительная погрешность – величина
безразмерная, чаще всего ее выражают в
процентах.

При
определении ошибок измерений важно
иметь в виду следующее. Выражения (1) и
(2) содержат истинное значение измеряемой
величины Х,
которое точно знать невозможно: поэтому
значения  х
и Е
в принципе не могут быть рассчитаны
точно. Можно лишь оценить
эти значения, т.е. найти их приближенно
с той или иной степенью достоверности.
Поэтому все расчеты, связанные с
определением погрешностей, должны
носить приближенный (оценочный) характер.

Случайная
и приборная погрешности

Разнообразные ошибки,
возникающие при измерениях, можно
классифицировать как по их происхождению,
так и по характеру их проявления.

По происхождению
ошибки делятся на инструментальные и
методические.

Инструментальные
погрешности обусловлены несовершенством
применяемых измерительных приборов и
приспособлений. Эти погрешности могут
быть уменьшены за счет применения более
точных приборов. Так, размер детали
можно измерить линейкой или штанген-циркулем.
Очевидно, что во втором случае ошибка
измерения меньше, чем в первом.

Методические
погрешности возникают из-за того, что
реальные физические процессы всегда в
той или иной степени отличаются от их
теоретических моделей. Например, формула
для периода колебаний математического
маятника в точности верна лишь при
бесконечно малой амплитуде колебаний;
формула Стокса, определяющая силу трения
при движении шарика в вязкой жидкости,
справедлива только в случае идеально
сферической формы и т.д. Обнаружить и
учесть методическую погрешность можно
путем измерения той же величины совершенно
иным независимым методом.

По характеру проявления
ошибки бывают систематические и
случайные.

Систематическая
погрешность может быть обусловлена как
приборами, так и методикой измерения.
Она имеет две характерные особенности.
Во-первых, систематическая погрешность
всегда либо положительна, либо отрицательна
и не меняет своего знака от опыта к
опыту. Во-вторых, систематическую
погрешность нельзя уменьшить за счет
увеличения числа измерений. Например,
если при отсутствии внешних воздействий
стрелка измерительного прибора показывает
величину х₀ , отличную от
нуля, то во всех дальнейших измерениях
будет присутствовать систематическая
ошибка, равная х₀ .

Случайная
ошибка также может быть как инструментальной,
так и методической. Причину ее появления
установить трудно, а чаще всего –
невозможно (это могут быть различные
помехи, случайные толчки, вибрации,
неверно взятый отсчет по прибору и
т.д.). Случайная погрешность бывает и
положительной и отрицательной, причем
непредсказуемо изменяет свой знак от
опыта к опыту. Значение ее можно уменьшить
путем увеличения числа измерений.

Детальный
анализ погрешностей измерения представляет
собой сложную задачу, для решения которой
не существует единого рецепта. Поэтому
в каждом конкретном случае этот анализ
проводят по-разному. Однако, в первом
приближении, если исключена систематическая
ошибка, то остальные можно условно
свести к следующим двум видам: приборная
и случайная.

Приборной
погрешностью в дальнейшем будем
называть случайную ошибку, обусловленную
измерительными приборами и приспособлениями,
а случайной – ошибку, причина
появления которой неизвестна. Приборную
погрешность измерения величины х
будем обозначать как  х,
случайную – как _s x.

Оценка
случайной погрешности. Доверительный
интервал

Методика оценки
случайной погрешности основана на
положениях теории вероятностей и
математической статистики. Оценить
случайную ошибку можно только в том
случае, когда проведено неоднократное
измерение одной и той же величины.

Пусть
в результате проделанных измерений
получено п
значений величины х:
х₁ ,
х₂ ,
…, х_п .
Обозначим через

среднеарифметическое значение

.
(3)

В
теории вероятностей доказано, что при
увеличении числа измерений п
среднеарифметическое значение измеряемой
величины приближается к истинному:

При
небольшом числе измерений (п  10)
среднее значение может существенно
отличаться от истинного. Для того, чтобы
знать, насколько точно значение

характеризует измеряемую величину,
необходимо определить так называемый
доверительный интервал полученного
результата.

Поскольку
абсолютно точное измерение невозможно,
то вероятность правильности утверждения
«величина х
имеет значение, в точности равное
»
равна нулю. Вероятность же утверждения
«величина х
имеет какое-либо значение»
равна единице (100%). Таким образом,
вероятность правильности любого
промежуточного утверждения лежит в
пределах от 0 до 1. Цель измерения – найти
такой интервал, в котором с наперед
заданной вероятностью 
(0 <  < 1)
находится истинное значение измеряемой
величины. Этот интервал называется
доверительным
интервалом,
а неразрывно связанная с ним величина

–
доверительной вероятностью
(или коэффициентом
надежности).
За середину интервала принимается
среднее значение, рассчитанное по
формуле (3). Половина ширины доверительного
интервала представляет собой случайную
погрешность _s x
(рис. 1).

Рис.1

Очевидно,
что
ширина доверительного интервала (а
следовательно, и ошибка _s x)
зависит от того, насколько сильно
отличаются отдельные измерения величины
х_i
от среднего
значения
.
«Разброс» результатов измерений
относительно среднего характеризуется
среднеквадратичной
ошибкой  ,
которую находят по формуле

,
(4)

где
.

Ширина
искомого доверительного интервала
прямо пропорциональна среднеквадратичной
ошибке:

.
(5)

Коэффициент
пропорциональности t_n,
называется
коэффициентом
Стьюдента;
он зависит от числа опытов п
и доверительной вероятности .

На
рис. 1, а, б
наглядно
показано, что при прочих равных условиях
для увеличения вероятности попадания
истинного значения в доверительный
интервал необходимо увеличить ширину
последнего (вероятность «накрывания»
значения Х
более широким интервалом выше).
Следовательно, величина t_n,
должна быть тем больше, чем выше
доверительная вероятность
 .

С
увеличением количества опытов среднее
значение приближается к истинному;
поэтому при той же вероятности 
доверительный интервал можно взять
более узким (см. рис. 1, а,в).
Таким образом, с ростом п
коэффициент Сьюдента должен
уменьшаться. Таблица значений коэффи-циента
Стьюдента в зависимости от п
и 
дана в приложениях к настоящему пособию.

Следует
отметить, что доверительная вероятность
никак не связана с точностью результата
измерений. Величиной 
задаются
заранее, исходя из требований к их
надежности. В большинстве технических
экспериментов и в лабораторном практикуме
значение 
принимается
равным 0,95.

Расчет
случайной погрешности измерения величины
х проводится
в следующем порядке:

1) вычисляется
сумма измеренных значений, а затем –
среднее значение величины

по формуле (3);

2) для
каждого i-го
опыта рассчитываются разность между
измеренным и средним значениями
,
а также квадрат этой разности (отклонения)
( х_i)² ;

3) находится
сумма квадратов отклонений, а затем –
средне-квадратичная ошибка 
по формуле (4);

4) по
заданной доверительной вероятности 
и числу
проведенных опытов п
из таблицы на с. 149 приложений выбирается
соответствующее значение коэффициента
Стьюдента t_n,
и определяется случайная погрешность
_s x
по формуле (5).

Для
удобства расчетов и проверки промежуточных
результатов данные заносятся в таблицу,
три последних столбца которой заполняются
по образцу табл.1.

Таблица
1

В
каждом конкретном случае величина х
имеет определенный физический смысл и
соответствующие единицы измерения. Это
может быть, например, ускорение свободного
падения g
(м/с²),
коэффициент вязкости жидкости 
(Пас)
и т.д. Пропущенные столбцы табл. 1
могут содержать промежуточные измеряемые
величины, необходимые для расчета
соответствующих значений х.

Пример
1. Для
определения ускорения а
движения тела измерялось время t
прохождения им пути S
без начальной
скорости. Используя известное соотношение
,
получим расчетную формулу

.
(6)

Результаты
измерений пути S
и времени t
приведены во втором и третьем столбцах
табл. 2. Проведя вычисления по формуле
(6), заполним

четвертый
столбец значениями ускорения a_i
и найдем их сумму, которую запишем под
этим столбцом в ячейку « 
= ». Затем рассчитаем среднее значение

по формуле (3)

.

Таблица
2

Вычитая
из каждого значения a_i
среднее, найдем разности  a_i

и занесем их в пятый столбец таблицы.
Возводя эти разности в квадрат, заполним
последний столбец. Затем рассчитаем
сумму квадратов отклонений и запишем
ее во вторую ячейку « 
= ». По формуле (4) определим
среднеквадратичную погрешность:

.

Задавшись
величиной доверительной вероятности
 = 0,95,
для числа опытов п = 4
из таблицы в приложениях (с. 149) выбираем
значение коэффициента Стьюдента t_n,
 = 3,18; с помощью формулы (5) оценим
случайную погрешность измерения
ускорения

_s а
= 3,180,0437  0,139 (м/с²) .

Способы
определения приборных ошибок

Основными характеристиками
измерительных приборов являются предел
измерения и цена деления, а также –
главным образом для электро-измерительных
приборов – класс точности.

Предел
измерения П
– это максимальное значение величины,
которое может быть измерено с помощью
данной шкалы прибора. Если
предел измерения не указан отдельно,
то его определяют по оцифровке шкалы.
Так, если рис. 2
изображает шкалу миллиамперметра, то
его предел измерения равен 100 мА.

Р
ис.2

Цена
деления Ц –
значение измеряемой величины,
соответствующее самому малому делению
шкалы. Если шкала начинается с нуля, то

,

где
N
– общее количество делений (например,
на рис. 2
N = 50).
Если эта шкала принадлежит амперметру
с пределом измерения 5 А,
то цена деления равна 5/50 = 0,1 (А).
Если шкала принадлежит термометру и
проградуирована в С,
то цена деления Ц = 100/50 = 2 (С).
Многие электроизмерительные приборы
имеют несколько пределов измерения.
При переключении их с одного предела
на другой изменяется и цена деления
шкалы.

Класс
точности К
представляет собой отношение абсолютной
приборной погрешности к пределу измерения
шкалы, выраженное в процентах:

.
(7)

Значение класса
точности (без символа «%») указывается,
как правило, на электроизмерительных
приборах.

В зависимости от вида
измерительного устройства абсолютная
приборная погрешность определяется
одним из нижеперечисленных способов.

1. Погрешность
указана непосредственно на приборе.
Так, на микрометре есть надпись «0,01 мм».
Если с помощью этого прибора измеряется,
например, диаметр шарика D
(лабораторная работа 1.2), то погрешность
его измерения D = 0,01 мм.
Абсолютная ошибка указывается обычно
на жидкостных (ртутных, спиртовых)
термометрах, штангенциркулях и др.

2. На приборе указан
класс точности. Согласно определению
этой величины, из формулы (7) имеем

.
(8)

Например, для вольтметра
с классом точности 2,5 и пределом измерения
600 В абсолютная приборная ошибка
измерения напряжения

.

3. Если на приборе
не указаны ни абсолютная погрешность,
ни класс точности, то в зависимости от
характера работы прибора возможны два
способа определения величины  х:

а) указатель
значения измеряемой величины может
занимать только определенные (дискретные)
положения, соответствующие делениям
шкалы (например, электронные часы,
секундомеры, счетчики импульсов и т.п.).
Такие приборы являются приборами
дискретного действия, и их абсолютная
погрешность равна цене деления шкалы:
 х = Ц.
Так, при измерении промежутка времени
t секундомером с ценой
деления 0,2 с погрешность  t = 0,2 с;

б) указатель
значения измеряемой величины может
занимать любое положение на шкале
(линейки, рулетки, стрелочные весы,
термометры и т.п.). В этом случае абсолютная
приборная погрешность равна половине
цены деления:  х = Ц/2.
Точность снимаемых показаний прибора
не должна превышать его возможностей.
Например, при показанном на рис. 3
положении стрелки прибора следует
записать либо 62,5 либо 63,0 – в обоих
случаях ошибка не превысит половины
цены деления. Записи же типа 62,7 или 62,8
не имеют смысла.

Рис.3

4. Если какая-либо
величина не измеряется в данном оыте,
а была измерена независимо и известно
лишь ее значение, то она является заданным
параметром. Так, в работе 2.1 по
определению коэффициента вязкости
воздуха такими параметрами являются
размеры капилляра, в опыте Юнга по
интерференции света (работа 5.1) –
расстояние между щелями и т.д. Погрешность
заданного параметра принимается равной
половине единицы последнего разряда
числа, которым задано значение этого
параметра. Например, если радиус капилляра
r задан с точностью
до сотых долей миллиметра, то его
погрешность  r = 0,005 мм.

Погрешности
косвенных измерений

В большинстве физических
экспериментов искомая величина и
не измеряется непосредственно каким-либо
одним прибором, а рассчитывается на
основе измерения ряда промежуточных
величин x, y, z,…
Расчет проводится по определенной
формуле, которую в общем виде можно
записать как

и = и ( x, y, z,…).
(9)

В этом случае говорят,
что величина и представляет собой
результат косвенного измерения в
отличие от x, y, z,…,
являющихся результатами прямых
измерений. Например, в
работе 1.2 коэффициент вязкости жидкости

рассчитывается по формуле

,
(10)

где _ш
– плотность материала шарика; _ж
– плотность жидкости; g
– ускорение свободного падения; D
– диаметр шарика; t –
время его падения в жидкости; l
– расстояние между метками на сосуде.
В данном случае результатами прямых
измерений являются величины l,
D и t,
а коэффициент вязкости 
– результат косвенного
измерения. Величины _ш,
_ж
и g представляют
собой заданные параметры.

Абсолютная
погрешность косвенного измерения  и
зависит от погрешностей прямых измерений
 x,
 y,
 z…и
от вида функции (9). Как правило, величину
 и
можно оценить по формуле
вида

,
(11)

где
коэффициенты k_x ,
k_y ,
k_z ,…
определяются видом зависимостей величины
и от x,
y, z,…
Приведенная ниже табл. 3 позволяет
найти эти коэффициенты для наиболее
распространенных элементарных функций
(a, b, c, n
– заданные константы).

Таблица
3

На
практике зависимость (9) чаще всего имеет
вид степенной функции

,

показатели степеней
которой k,
m, n,…
– вещественные (положительные или
отрицательные, целые или дробные) числа;
С – постоянный коэффициент. В этом
случае абсолютная приборная погрешность
 и
оценивается по формуле

,
(12)

где

– среднее значение величины и;

– относительные приборные погрешности
прямых измерений величин x,
y, z,…
Для подстановки в формулу (12) выбираются
наиболее представительные, т.е.
близкие к средним значения x,
y, z,…

При расчетах по
формулам типа (12) необходимо помнить
следующее.

1. Измеряемые
величины и их абсолютные погрешности
(например, х и  х)
должны быть выражены в одних и тех же
единицах.

2. Расчеты не требуют
высокой точности вычислений и должны
иметь оценочный характер. Так, входящие
в подкоренное выражение и возводимые
в квадрат величины ( kE_x ,
 mE_y ,
 nE_z ,…)
обычно округляются с точностью до
двух значащих цифр (напомним, что ноль
является значащей цифрой только тогда,
когда перед ним слева есть хотя бы одна
цифра, отличная от нуля). Далее, если
одна из этих величин (например, | kE_x | ) по
модулю превышает наибольшую из остальных
( | mE_y | ,
 | nE_z | ,…)
более чем в три раза, то можно, не прибегая
к вычислениям по формуле (12), принять
абсолютную ошибку равной
.
Если же одна из них более чем в три раза
меньше наименьшей из остальных, то при
расчете по формуле (12) ею можно пренебречь.

Пример 2.
Пусть при определении ускорения тела
(см. пример 1) путь S
измерялся рулеткой с ценой деления
1 мм, а время t
– электронным секундомером. Тогда, в
соответствии с изложенными в п.3, а, б
(с. 13) правилами, погрешности прямых
измерений будут равны

 S = 0,5 мм = 0,0005 м;

 t = 0,01 с.

Расчетную формулу
(6) можно записать в виде степенной
функции

a( S, t ) = 2S ¹t ^– 2 ;

тогда на основании
(12) погрешность косвенного измерения
ускорения  а
определится выражением

.

В
качестве наиболее представительных
значений измеренных величин возьмем
(см. табл. 2) S  8 м;
t  3 с
и оценим по модулю относительные
приборные ошибки прямых измерений с
учетом их весовых коэффициентов:

;

.

Очевидно,
что в данном случае величиной E_S
можно пренебречь и принять погрешность
 а
равной

Пример 3.
Вернемся к определению коэффициента
вязкости жидкости (работа 1.2). Расчетную
формулу (10) можно представить в виде

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Погре́шность измере́ния — оценка отклонения величины измеренного значения величины от её истинного значения. Погрешность измерения является характеристикой (мерой) точности измерения.

Поскольку выяснить с абсолютной точностью истинное значение любой величины невозможно, то невозможно и указать величину отклонения измеренного значения от истинного. (Это отклонение принято называть ошибкой измерения. В ряде источников, например, в БСЭ, термины ошибка измерения и погрешность измерения используются как синонимы.) Возможно лишь оценить величину этого отклонения, например, при помощи статистических методов. При этом за истинное значение принимается среднестатистическое значение, полученное при статистической обработке результатов серии измерений. Это полученное значение не является точным, а лишь наиболее вероятным. Поэтому в измерениях необходимо указывать, какова их точность. Для этого вместе с полученным результатом указывается погрешность измерений. Например, запись T=2.8±0.1 c. означает, что истинное значение величины T лежит в интервале от 2.7 с. до 2.9 с. некоторой оговоренной вероятностью (см. доверительный интервал, доверительная вероятность, стандартная ошибка).

В 2006 году на международном уровне был принят новый документ, диктующий условия проведения измерений и установивший новые правила сличения государственных эталонов. Понятие «погрешность» стало устаревать, вместо него было введено понятие «неопределенность измерений».

Определение погрешности

В зависимости от характеристик измеряемой величины для определения погрешности измерений используют различные методы.

• Метод Корнфельда, заключается в выборе доверительного интервала в пределах от минимального до максимального результата измерений, и погрешность как половина разности между максимальным и минимальным результатом измерения:

• Средняя квадратическая погрешность:

• Средняя квадратическая погрешность среднего арифметического:

Классификация погрешностей

По форме представления

• Абсолютная погрешность — ΔX является оценкой абсолютной ошибки измерения. Величина этой погрешности зависит от способа её вычисления, который, в свою очередь, определяется распределением случайной величины X_meas. При этом равенство:

ΔX = | X_true − X_meas | ,

где X_true — истинное значение, а X_meas — измеренное значение, должно выполняться с некоторой вероятностью близкой к 1. Если случайная величина X_meas распределена по нормальному закону, то, обычно, за абсолютную погрешность принимают её среднеквадратичное отклонение. Абсолютная погрешность измеряется в тех же единицах измерения, что и сама величина.

• Относительная погрешность — отношение абсолютной погрешности к тому значению, которое принимается за истинное:

.

Относительная погрешность является безразмерной величиной, либо измеряется в процентах.

• Приведенная погрешность — относительная погрешность, выраженная отношением абсолютной погрешности средства измерений к условно принятому значению величины, постоянному во всем диапазоне измерений или в части диапазона. Вычисляется по формуле

,

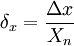
где X_n — нормирующее значение, которое зависит от типа шкалы измерительного прибора и определяется по его градуировке:

— если шкала прибора односторонняя, т.е. нижний предел измерений равен нулю, то X_n определяется равным верхнему пределу измерений;
— если шкала прибора двухсторонняя, то нормирующее значение равно ширине диапазона измерений прибора.

Приведенная погрешность — безразмерная величина (может измеряться в процентах).

По причине возникновения

• Инструментальные / приборные погрешности — погрешности, которые определяются погрешностями применяемых средств измерений и вызываются несовершенством принципа действия, неточностью градуировки шкалы, ненаглядностью прибора.
• Методические погрешности — погрешности, обусловленные несовершенством метода, а также упрощениями, положенными в основу методики.
• Субъективные / операторные / личные погрешности — погрешности, обусловленные степенью внимательности, сосредоточенности, подготовленности и другими качествами оператора.

В технике применяют приборы для измерения лишь с определенной заранее заданной точностью – основной погрешностью, допускаемой нормали в нормальных условиях эксплуатации для данного прибора.

Если прибор работает в условиях, отличных от нормальных, то возникает дополнительная погрешность, увеличивающая общую погрешность прибора. К дополнительным погрешностям относятся: температурная, вызванная отклонением температуры окружающей среды от нормальной, установочная, обусловленная отклонением положения прибора от нормального рабочего положения, и т.п. За нормальную температуру окружающего воздуха принимают 20°С, за нормальное атмосферное давление 01,325 кПа.

Обобщенной характеристикой средств измерения является класс точности, определяемый предельными значениями допускаемых основной и дополнительной погрешностей, а также другими параметрами, влияющими на точность средств измерения; значение параметров установлено стандартами на отдельные виды средств измерений. Класс точности средств измерений характеризует их точностные свойства, но не является непосредственным показателем точности измерений, выполняемых с помощью этих средств, так как точность зависит также от метода измерений и условий их выполнения. Измерительным приборам, пределы допускаемой основной погрешности которых заданы в виде приведенных основных (относительных) погрешностей, присваивают классы точности, выбираемые из ряда следующих чисел: (1; 1,5; 2,0; 2,5; 3,0; 4,0; 5,0; 6,0)*10n, где n = 1; 0; -1; -2 и т.д.

По характеру проявления

• Случайная погрешность — погрешность, меняющаяся (по величине и по знаку) от измерения к измерению. Случайные погрешности могут быть связаны с несовершенством приборов (трение в механических приборах и т.п.), тряской в городских условиях, с несовершенством объекта измерений (например, при измерении диаметра тонкой проволоки, которая может иметь не совсем круглое сечение в результате несовершенства процесса изготовления), с особенностями самой измеряемой величины (например при измерении количества элементарных частиц, проходящих в минуту через счётчик Гейгера).
• Систематическая погрешность — погрешность, изменяющаяся во времени по определенному закону (частным случаем является постоянная погрешность, не изменяющаяся с течением времени). Систематические погрешности могут быть связаны с ошибками приборов (неправильная шкала, калибровка и т.п.), неучтёнными экспериментатором.
• Прогрессирующая (дрейфовая) погрешность — непредсказуемая погрешность, медленно меняющаяся во времени. Она представляет собой нестационарный случайный процесс.
• Грубая погрешность (промах) — погрешность, возникшая вследствие недосмотра экспериментатора или неисправности аппаратуры (например, если экспериментатор неправильно прочёл номер деления на шкале прибора, если произошло замыкание в электрической цепи).

По способу измерения

• Погрешность прямых измерений
• Погрешность косвенных измерений — погрешность вычисляемой (не измеряемой непосредственно) величины:

Если F = F(x₁,x₂…x_n), где x_i — непосредственно измеряемые независимые величины, имеющие погрешность Δx_i, тогда:

См. также

• Измерение физических величин
• Класс точности
• Метрология
• Система автоматизированного сбора данных со счетчиков по радиоканалу
• Методы электроаналитической химии

Литература

• Назаров Н. Г. Метрология. Основные понятия и математические модели. М.: Высшая школа, 2002. 348 с.

• Лабораторные занятия по физике. Учебное пособие/Гольдин Л. Л., Игошин Ф. Ф., Козел С. М. и др.; под ред. Гольдина Л. Л. — М.: Наука. Главная редакция физико-математичекой литературы, 1983. — 704 с.

Статья обновлена 10.07.2022

Что такое погрешность измерения

Любой расчет состоит из истинного и вычисляемого значения. При этом всегда должны учитываться значения ошибки или погрешности. Погрешность — это расхождение между истинным значением и вычисляемым. В маркетинге выделяют следующие виды погрешностей.

1. Математическая погрешность. Она описывается алгебраической формулой и бывает абсолютной, относительной и приведенной. Абсолютная погрешность измерения — это разница между вычисляемым и истинным значением. Относительная погрешность вычисляется в процентном соотношении истинного значения и полученного. Вычисление погрешности приведенной схоже с относительной, указывается она также в процентах, но дает разницу между нормирующей шкалой и полученными данными, то есть между эталонными и полученными значениями.
2. Оценочная погрешность. В маркетинге она бывает случайной и систематической. Случайная погрешность возникает из-за любых факторов, которые случайным образом влияют на измерение переменной в выборке. Систематическая погрешность вызывается факторами, которые систематически влияют на измерение переменной в выборке.

Математическая погрешность: формула для каждого типа

Если определение погрешности можно провести точным путем, она считается математической. Зачем нужно вычисление этого значения в маркетинге?

Погрешности возникают настолько часто, что популярной практикой в исследованиях является включение значения погрешности в окончательные результаты. Для этого используются формулы. Математическая погрешность — это значение, которое отражает разницу между выборкой и фактическим результатом. Если при расчетах учитывалась  погрешность, в тексте исследования указывается что-то вроде: «Абсолютная погрешность для этих данных составляет 3,25%». Погрешность можно вычислить с любыми цифрами: количество человек, участвующих в опросе, погрешность суммы, затраченной на маркетинговый бюджет, и так далее.

Формулы погрешностей вычисляются следующим образом.

Абсолютная погрешность измерений: формула

Формула дает разницу между измеренным и реальным значением.

Относительная погрешность: формула

Формула использует значение абсолютной погрешности и вычисляется в процентах по отношению к фактическому  значению.

Приведенная погрешность: формула

Формула также использует значение абсолютной погрешности. В чем измеряется приведенная погрешность? Тоже в процентах, но в качестве «эталона» используется не реальное значение, а единица измерения любой нормирующей шкалы. Например, для обычной линейки это значение равно 1 мм.

Классификация оценочной погрешности

Определение погрешности в оценках — это всегда методическая погрешность, то есть допустимое значение ошибки, основанное на методах проведения исследования. Погрешность метода вызывает два типа погрешностей — случайные и систематические. Таблица погрешностей в графической форме покажет все возможные типы.

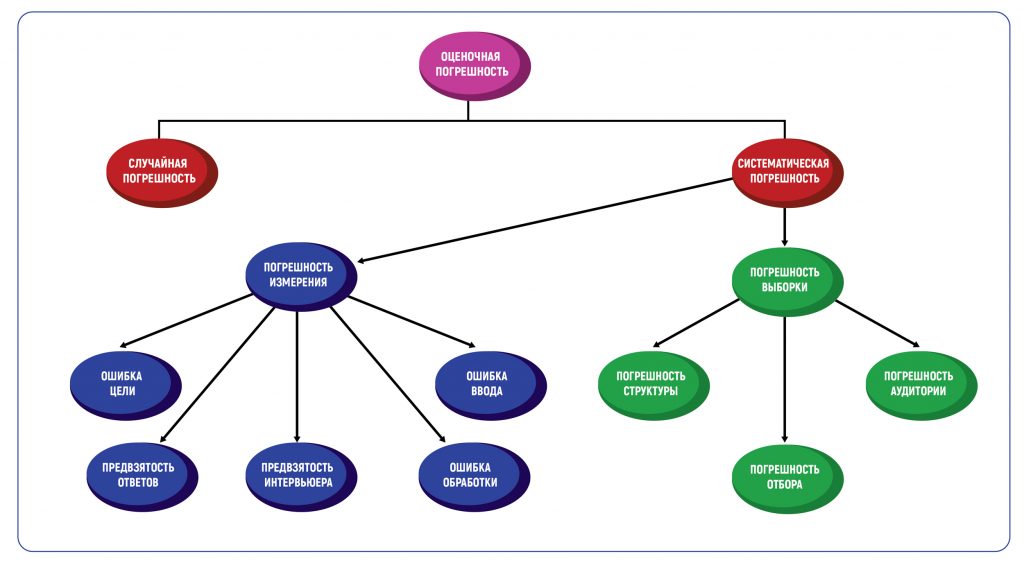
Что такое случайная погрешность

Случайная погрешность бывает статической и динамической. Динамическая погрешность возникает, когда мы имеем дело с меняющимися значениями — например, количество человек в выборке при маркетинговом исследовании. Статическая погрешность описывает ошибки при вычислении неизменных величин — вроде количества вопросов в вопроснике. Все они относятся к случайным погрешностям.

Типичный пример возникновения случайной погрешности — настроение участников маркетингового опроса. Как известно, эмоциональный настрой человека всегда влияет на его производительность. В ходе тестирования одни люди могут быть в хорошем расположении духа, а другие — в «миноре». Если настроение влияет на их ответы по заданному критерию выборки, это может искусственно завышать или занижать наблюдаемые оценки. Например, в случае с истинным значением 1 случайная погрешность может дать как -0,8, так и +0,5 к этому числу. Очень часто это случается при оценке времени ответа, например.

Случайная погрешность добавляет изменчивости данным, но не оказывает постоянного влияния на всю выборку. Вместо этого она произвольно изменяет измеряемые значения в диапазоне. В маркетинговой практике считается, что все случайные погрешности в распределении перекрывают друг друга и практически не влияют на конечный результат. Поэтому случайная погрешность считается «шумом» и в расчет не принимается. Эту погрешность нельзя устранить совсем, но можно уменьшить, просто увеличив размер выборки.

Что такое систематическая погрешность

Систематическая погрешность существует в результатах исследования, если эти результаты показывают устойчивую тенденцию к отклонению от истинных значений. Иными словами, если полученные цифры постоянно выше или ниже расчетных, речь идет о том, что в данных имеется систематическая погрешность.

В маркетинговых исследованиях есть два основных типа систематической погрешности: погрешность выборки и погрешность измерения. 

Погрешность выборки

Погрешность выборки возникает, когда выборка, используемая в исследовании, не репрезентативна для всей совокупности данных. Типы такой погрешности включают погрешность структуры, погрешность аудитории и погрешность отбора.

Погрешность структуры

Погрешность структуры возникает из-за использования неполной или неточной основы для выборки. Распространенным источником такой погрешности в рамках маркетинговых исследований является проведение какого-либо опроса по телефону на основе существующего телефонного справочника или базы данных абонентов. Многие данные там указаны неполно или неточно — например, если люди недавно переехали или изменили свой номер телефона. Также такие данные часто указывают неполную или неверную демографию.

Если в качестве основы для исследования взят телефонный справочник, оно подвержено погрешности структуры, так как не учитывает всех возможных респондентов.

Погрешность аудитории

Погрешность аудитории возникает, если исследователь не знает, как определить аудиторию для исследования. Пример — оценка результатов исследования, проведенного среди клиентов крупного банка. Доля ответов на анкету составила чуть менее 1%. Анализ профессий всех опрошенных показал, что процент пенсионеров среди них в 20 раз выше, чем в целом по городу. Если эта группа значительно различается по интересующим переменным, то результаты будут неверными из-за погрешности аудитории.

Погрешность отбора

Даже если маркетологи правильно определили структуру и аудиторию, они не застрахованы от погрешности отбора. Она возникает, когда процедуры отбора являются неполными, неправильными или не соблюдаются должным образом. Например, интервьюеры при полевом исследовании могут избегать людей, которые живут в муниципальных домах. Потому что, по их мнению, жители вряд ли согласятся пройти такой опрос. Если жители муниципальных домов отличаются от тех, кто проживает в домах бизнес-класса, в результаты опроса будет внесена погрешность отбора.

Как минимизировать погрешность выборки

• Знайте свою аудиторию.
  Знайте, кто покупает ваш продукт, использует его, работает с вами и так далее. Имея базовую социально-экономическую информацию, можно составить стабильную выборку целевой аудитории. Маркетинговые исследования часто касаются одной конкретной группы населения — например, пользователей Facebook или молодых мам.
• Разделите аудиторию на группы.
  Вместо случайной выборки разбейте аудиторию на группы в соответствии с их численностью в общей совокупности данных. Например, если люди с определенной демографией составляют 35% населения, убедитесь, что 35% респондентов исследования отвечают этому условию.
• Увеличьте размер выборки.
  Больший размер выборки приводит к более точному результату.

Погрешность измерения

Погрешность измерения представляет собой серьезную угрозу точности исследования. Она возникает, когда существует разница между искомой информацией — то есть истинным значением, и информацией, фактически полученной в процессе измерения. К таким погрешностям приводят различные недостатки процесса исследования. Погрешность измерения, в основном, вызывается человеческим фактором — например, формулировкой вопросника, ошибками ввода данных и необъективными выводами.

К погрешностям измерения приводят следующие виды ошибок.

Ошибка цели

Ошибка цели возникает, когда существует несоответствие между информацией, фактически необходимой для решения проблемы, и данными , которые собирает исследование. Например, компания Kellogg впустую потратила миллионы на разработку завтраков для снижения уровня холестерина. Реальный вопрос, который нужно было бы задать в исследовании, заключался в том, купят ли люди овсяные хлопья для решения своей проблемы. Ответ «Нет» обошелся бы компании дешевле.

Предвзятость ответов

Некоторые люди склонны отвечать на конкретный вопрос определенным образом. Тогда возникает предвзятость ответа. Предвзятость ответа может быть результатом умышленной фальсификации или неосознанного искажения фактов.

Умышленная фальсификация происходит, когда респонденты целенаправленно дают неверные ответы на вопросы. Есть много причин, по которым люди могут сознательно искажать информацию. Например, они хотят скрыть  или хотят казаться лучше, чем есть на самом деле.

Бессознательное искажение информации происходит, когда респондент пытается быть правдивым, но дает неточный ответ. Этот тип предвзятости может возникать из-за формата вопроса, его содержания или по другим причинам.

Предвзятость интервьюера

Интервьюер оказывает влияние на респондента — сознательно или бессознательно. Одежда, возраст, пол, выражение лица, язык тела или тон голоса могут повлиять на ответы некоторых или всех респондентов.

Ошибка обработки

Примеры включают наводящие вопросы или элементы дизайна анкеты, которые затрудняют запись ответов или приводят к ошибкам в них.

Ошибка ввода

Это ошибки, возникающие при вводе информации. Например, документ может быть отсканирован неправильно, и его данные по ошибке перенесутся неверно. Или люди, заполняющие опросы на смартфоне или ноутбуке, могут нажимать не те клавиши.

Виды проводимых маркетинговых исследований различны, поэтому универсальных рецептов не существует. Мы дадим несколько общих советов, используемых для минимизации систематических погрешностей разного типа.

Как минимизировать погрешность измерения

• Предварительно протестируйте.
  Погрешностей обработки и предвзятости можно избежать, если проводить предварительные тесты вопросника до начала основных интервью.
• Проводите выборку случайным образом.
  Чтобы устранить предвзятость, при выборке респондентов можно включать каждого четвертого человека из общего списка.
• Тренируйте команду интервьюеров и наблюдателей.
  Отбор и обучение тех, кто проводит исследования, должен быть тщательным. Особое внимание нужно уделять соблюдению инструкций в ходе каждого исследования.
• Всегда выполняйте проверку сделанных записей.
  Чтобы исключить ошибки ввода, все данные, вводимые для компьютерного анализа, должны быть перепроверены как минимум дважды.

Мир без ошибок  не может существовать. Но понимание факторов, влияющих на маркетинговые исследования и измеряемые погрешности, имеет важное значение для сбора качественных данных.