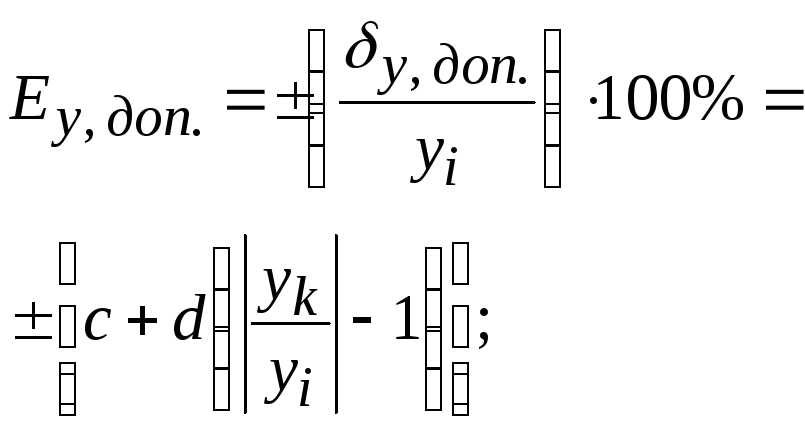Среднее квадратическое отклонение результата наблюдения Средняя квадратическая (квадратичная) погрешность (ошибка) единичного измерения. Среднеквадратичная погрешность (ошибка) стандарт измерений Параметр функции распределения результатов наблюдений, характеризующий их рассеивание и равный корню квадратному из дисперсии результата наблюдения (с положительным знаком) [c.95]
ОШИБКА ЕДИНИЧНОГО ИЗМЕРЕНИЯ
[c.66]
Затем находятся дисперсия и стандартная ошибка единичного наблюдения. Из числа наблюдений исключаются единичные наблюдения, у которых отклонение от среднего значения больше За. После этого проводится второе приближение, для чего определяется среднее арифметическое значение от оставшихся измерений и определяется новое значение стандартной ошибки единичного измерения и снова определяется величина предельной ошибки Зст.
[c.31]
Таким образом, в данном примере оказалось, что ошибка среднего арифметического в 5 раз меньше, чем ошибка единичных измерений, из которых складывается среднее арифметическое.
[c.33]
Среднее квадратическое значение ошибки единичного измерения углов а и i составляет 0а = 45″ и Стз = 60″.
[c.314]
Указание только одной величины ошибки единичного измерения 5 без соответствующей ей доверительной вероятности в значительной мере лишено смысла, так как при этом неясно, насколько надежны полученные данные [6].
[c.32]
Вероятная ошибка единичного измерения. ……..
[c.195]
Рассчитанная по (8) и (9) вероятная ошибка единичного измерения скорости звука по изобарам при температурах 825—1275° К и давлениях 0,358—5,303 атм изменяется от 0,32 до 0,34%. Среднеквадратичное отклонение экспериментальных данных по изобарам в указанном диапазоне температур и давлений не превышает 0,3%.
[c.116]
Определение нескольких экспериментальных точек кривой к=к Р ) позволяет свести к минимуму возможные ошибки при единичных измерениях. Полученные в опытах [38, 71] значения параметров 6 и V сопоставлялись с расчетом. В табл. 17 приведены результаты эксперимента. На основании эксперимента были рассчитаны значения к/г и и представлены на фиг. 23 в виде точек. Результаты расчета и эксперимента удовлетворительно совпадают.
[c.47]
Максимальная относительная флуктуационная ошибка ( Ар/р)фд единичного измерения плотности газа может быть вычислена по формуле
[c.282]
На рис. 4-2 представлены изменение во времени истинного значения исследуемого параметра х и случайная погрешность системы измерений этого параметра Ах. Таким образом, наблюдаемая при измерении величина содержит как ошибки собственно измерений, так и ошибки в определении исследуемого параметра, вызванные его отклонениями от равновесного состояния. Как видно из графика, единичный замер может совпасть как с максимальным отклонением исследуемого параметра, так и с максимальной величиной ошибки прибора. 4—1368 49
[c.49]
Случайная ошибка среднего арифметического ряда наблюдений в 1 /I/» п, раз меньше ошибки единичного наблюдения (измерения). Если принять ошибку единичного наблюдения за 1,0, то при четырех наблюдениях она снизится в 2 раза, при девяти — в 3 раза, при 16— в 4 раза и т. д. Таким образом, при очень большом числе наблюдений случайная ошибка среднего арифметического стремится к нулю. Само собой разумеется, что никакое увеличение числа наблюдений не спасает нас от систематических ошибок. Негативная сторона большого числа наблюдений состоит в том, что они вызывают удорожание опыта и рост его продолжительности.
[c.73]
Средняя абсолютная квадратичная ошибка единичного результата при п измерениях представляется зависимостью
[c.248]
По результатам измерений величин d и Л установлено среднее значение диаметра цилиндра (i p 9.12 мм, среднее значение высоты цилиндра Лдо = 16,22 мм, средние квадратические значения ошибок единичных измерений диаметра и высоты цилиндра = 0,008 мм, a i — 0,012 мм. Средние квадратические ошибки определения средних арифметических значений диаметра d и высоты h цилиндра [c.314]
Метод позволяет получать небольшую погрешность отсчета и определять ошибку всей шкалы. При единичном измерении ненадежность i=ih3 мк, а при серии— = > 1,5 мк. Проверка этим способом, в противоположность проверке по концевым мерам, может производиться при движении стержня в обоих направлениях.
[c.378]
Ошибка единичного основного шага /е— разность между его действительным и предписанным значениями. Это измерение безотносительно, т. е. независимо от эксцентрицитета основной окружности относительно оси вращения. Единичная ошибка окружного шага f — разность между действительным размером единичного окружного шага и его предписанным размером, измеренная по дуге делительной окружности с центром, лежащим на оси колеса.
[c.637]
Погрешности метода происходят вследствие ошибок или недостаточной разработанности метода измерений. Сюда же можно отнести неправомерную экстраполяцию свойства, полученного в результате единичного измерения, на весь измеряемый объект. Например, принимая решение о годности вала по единичному измерению, можно допустить ошибку, поскольку не учитываются такие погрещности формы, как отклонения от цилиндричности, круглости, профиля продольного сечения и др. Поэтому для исключения такого рода систематических погрешностей в методике измерений рекомендуется проведение измерений в нескольких местах деталей и взаимно-перпендикулярных направлениях.
[c.271]
Остановимся на указанном вопросе несколько подробнее. Допустим, что исследуется зависимость сопротивления от расхода. Так как расход и сопротивление измеряются разными приборами, имеющими каждый свои случайные ошибки, полученные величины не будут истинными. Можно, однако, полагать, что каждое единичное значение расхода Xi является истинным, а случайно, т. е. имеет ошибку, только сопротивление. Если бы сопротивление не зависело от расхода, подобное допущение не привело бы нас к ошибке, так как безразлично, к какому значению расхода отнесено данное сопротивление. Поскольку, однако, такая зависимость есть, ошибка измерения расхода х приведет к появлению дополнительной ошибки величины сопротивления
[c.89]
Осуществим первую оценку достоверности измерений. Уже указывалось, что единичное наблюдение признается промахом или грубой ошибкой, если его отклонение от среднего уровня больше За. В нашем случае
[c.95]
Средняя арифметическая и средняя квадратичная ошибки. При проведении экспериментов каждый единичный опыт следует повторить достаточное число раз, чтобы случайные ошибки результата были незначительными по сравнению с систематическими. При проведении п измерений единичного результата среднее арифметическое величин 1, 2, из,. .., 71 составит [c.247]
Публикации Купфера в высшей степени трудны для чтения не только потому, что они содержат многочисленные ошибки, часть из которых была замечена другими, и значительное количество неясных рассуждений ), но также потому, что он избрал путь представления упругости твердого тела в терминах одной постоянной, и эта постоянная введена исключительно неудобным способом. Использование постоянной, обозначенной через б, указывает на возвращение к состоянию знаний начала XIX века, так как ее значение зависело от формы поперечного сечения, а также в неявном виде от единицы измерения приложенной силы. Для продольного нагружения цилиндрического стержня постоянная б определялась как удлинение, вызываемое единичной силой, приложенной к круглому цилиндрическому образцу единичной длины с единичным радиусом, т. е. 6=1/(ir ). Для стержня квадратного поперечного сечения постоянная б определялась как удлинение, вызываемое единичной силой, приложенной к стержню единичной длины с единичными сторонами поперечного сечения. Для стержня прямоугольного поперечного сечения б=1/ . Для последнего вида стержней в некоторых случаях, но, к сожалению, не всегда, Купфер использовал символ б. Он представил некоторые из своих результатов в русских фунтах и русских дюймах ). В других случаях он выражал б в сантиметрах, приложенную нагрузку — в граммах, а в одном случае он использовал английские единицы измерения. Как косвенно признал даже сам Купфер в подстрочном
[c.392]
Единичная ошибка шага (шага делительной окружности) — разность между действительным и предписанным размерами единичного шага делительной окружности, измеренная по делительной окружности, с центром, совпадающим с осью колеса.
[c.311]
Яя шага Измеренное значе ие в мк Единичная ошибка шага в мк Суммарная ошибка в мк Приращение шага в мк
[c.642]
Используя данные о классе точности применявшихся приборов и отдельных узлов измерительной схемы, рассчитывали погрешность определения теплоемкости относительная ошибка единичного измерения оказалась равной 2%. Была вычислена также дисперсия многочисленных экспериментальных данных, полученных описанным методом. Найденная в результате статистической обработки погрешность, определяемая двухсигмовым интервалом, равна 5%. Такое различие вызвано тем, что в аналитическом расчете ошибки не
[c.73]
При измерении зубчатых колес пли делительных дисков для установки используется угловой рычаг, который устанавливается по профилю зуба и при повороте стола перед каждым измерением ставится в нулевое положение. При повороте теодолита отметки па нем и коллиматоре совмещаются. Затем отсчитывают углы. После этого поворачивают стол от зуба к зубу илн на определенное число шагов. Прн точных проверках рычажный прибор снова устанавливается на ноль и настривают коллиматор с теодолито.м. Разность между отсчетами по лимбу и предписанными значениями дает ошибку шага. Ненадежность единичного измерения примерно (0,01го+ ) мк, где г а — в мм.
[c.643]
Измерения пробного колеса должны производиться с наибольшей возможной точностью. Построение графика накоплен ной ошибки окрул<ного шага по результатам обработки измерений единичных шагов недопустимо необходимо непосредственное измерение накопленных ошибок, например при помощи теодолита.
[c.634]
О непосредственном измерении сум.марнон ошибки шага см. 63—[ 12]. Так как при суммировании единичных ошибок их ошибки также алгебраически сум.мируются, то целесообразно суммарную ошибку опре-
[c.642]
Погре́шность измере́ния — оценка отклонения величины измеренного значения величины от её истинного значения. Погрешность измерения является характеристикой (мерой) точности измерения.
Поскольку выяснить с абсолютной точностью истинное значение любой величины невозможно, то невозможно и указать величину отклонения измеренного значения от истинного. (Это отклонение принято называть ошибкой измерения. В ряде источников, например, в БСЭ, термины ошибка измерения и погрешность измерения используются как синонимы.) Возможно лишь оценить величину этого отклонения, например, при помощи статистических методов. При этом за истинное значение принимается среднестатистическое значение, полученное при статистической обработке результатов серии измерений. Это полученное значение не является точным, а лишь наиболее вероятным. Поэтому в измерениях необходимо указывать, какова их точность. Для этого вместе с полученным результатом указывается погрешность измерений. Например, запись T=2.8±0.1 c. означает, что истинное значение величины T лежит в интервале от 2.7 с. до 2.9 с. некоторой оговоренной вероятностью (см. доверительный интервал, доверительная вероятность, стандартная ошибка).
В 2006 году на международном уровне был принят новый документ, диктующий условия проведения измерений и установивший новые правила сличения государственных эталонов. Понятие «погрешность» стало устаревать, вместо него было введено понятие «неопределенность измерений».
Содержание
- 1 Определение погрешности
- 2 Классификация погрешностей
- 2.1 По форме представления
- 2.2 По причине возникновения
- 2.3 По характеру проявления
- 2.4 По способу измерения
- 3 См. также
- 4 Литература
Определение погрешности
В зависимости от характеристик измеряемой величины для определения погрешности измерений используют различные методы.
- Метод Корнфельда, заключается в выборе доверительного интервала в пределах от минимального до максимального результата измерений, и погрешность как половина разности между максимальным и минимальным результатом измерения:
- Средняя квадратическая погрешность:
- Средняя квадратическая погрешность среднего арифметического:
Классификация погрешностей
По форме представления
- Абсолютная погрешность — ΔX является оценкой абсолютной ошибки измерения. Величина этой погрешности зависит от способа её вычисления, который, в свою очередь, определяется распределением случайной величины Xmeas. При этом равенство:
ΔX = | Xtrue − Xmeas | ,
где Xtrue — истинное значение, а Xmeas — измеренное значение, должно выполняться с некоторой вероятностью близкой к 1. Если случайная величина Xmeas распределена по нормальному закону, то, обычно, за абсолютную погрешность принимают её среднеквадратичное отклонение. Абсолютная погрешность измеряется в тех же единицах измерения, что и сама величина.
- Относительная погрешность — отношение абсолютной погрешности к тому значению, которое принимается за истинное:

Относительная погрешность является безразмерной величиной, либо измеряется в процентах.
- Приведенная погрешность — относительная погрешность, выраженная отношением абсолютной погрешности средства измерений к условно принятому значению величины, постоянному во всем диапазоне измерений или в части диапазона. Вычисляется по формуле
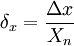
где Xn — нормирующее значение, которое зависит от типа шкалы измерительного прибора и определяется по его градуировке:
— если шкала прибора односторонняя, т.е. нижний предел измерений равен нулю, то Xn определяется равным верхнему пределу измерений;
— если шкала прибора двухсторонняя, то нормирующее значение равно ширине диапазона измерений прибора.
Приведенная погрешность — безразмерная величина (может измеряться в процентах).
По причине возникновения
- Инструментальные / приборные погрешности — погрешности, которые определяются погрешностями применяемых средств измерений и вызываются несовершенством принципа действия, неточностью градуировки шкалы, ненаглядностью прибора.
- Методические погрешности — погрешности, обусловленные несовершенством метода, а также упрощениями, положенными в основу методики.
- Субъективные / операторные / личные погрешности — погрешности, обусловленные степенью внимательности, сосредоточенности, подготовленности и другими качествами оператора.
В технике применяют приборы для измерения лишь с определенной заранее заданной точностью – основной погрешностью, допускаемой нормали в нормальных условиях эксплуатации для данного прибора.
Если прибор работает в условиях, отличных от нормальных, то возникает дополнительная погрешность, увеличивающая общую погрешность прибора. К дополнительным погрешностям относятся: температурная, вызванная отклонением температуры окружающей среды от нормальной, установочная, обусловленная отклонением положения прибора от нормального рабочего положения, и т.п. За нормальную температуру окружающего воздуха принимают 20°С, за нормальное атмосферное давление 01,325 кПа.
Обобщенной характеристикой средств измерения является класс точности, определяемый предельными значениями допускаемых основной и дополнительной погрешностей, а также другими параметрами, влияющими на точность средств измерения; значение параметров установлено стандартами на отдельные виды средств измерений. Класс точности средств измерений характеризует их точностные свойства, но не является непосредственным показателем точности измерений, выполняемых с помощью этих средств, так как точность зависит также от метода измерений и условий их выполнения. Измерительным приборам, пределы допускаемой основной погрешности которых заданы в виде приведенных основных (относительных) погрешностей, присваивают классы точности, выбираемые из ряда следующих чисел: (1; 1,5; 2,0; 2,5; 3,0; 4,0; 5,0; 6,0)*10n, где n = 1; 0; -1; -2 и т.д.
По характеру проявления
- Случайная погрешность — погрешность, меняющаяся (по величине и по знаку) от измерения к измерению. Случайные погрешности могут быть связаны с несовершенством приборов (трение в механических приборах и т.п.), тряской в городских условиях, с несовершенством объекта измерений (например, при измерении диаметра тонкой проволоки, которая может иметь не совсем круглое сечение в результате несовершенства процесса изготовления), с особенностями самой измеряемой величины (например при измерении количества элементарных частиц, проходящих в минуту через счётчик Гейгера).
- Систематическая погрешность — погрешность, изменяющаяся во времени по определенному закону (частным случаем является постоянная погрешность, не изменяющаяся с течением времени). Систематические погрешности могут быть связаны с ошибками приборов (неправильная шкала, калибровка и т.п.), неучтёнными экспериментатором.
- Прогрессирующая (дрейфовая) погрешность — непредсказуемая погрешность, медленно меняющаяся во времени. Она представляет собой нестационарный случайный процесс.
- Грубая погрешность (промах) — погрешность, возникшая вследствие недосмотра экспериментатора или неисправности аппаратуры (например, если экспериментатор неправильно прочёл номер деления на шкале прибора, если произошло замыкание в электрической цепи).
По способу измерения
- Погрешность прямых измерений
- Погрешность косвенных измерений — погрешность вычисляемой (не измеряемой непосредственно) величины:
Если F = F(x1,x2…xn), где xi — непосредственно измеряемые независимые величины, имеющие погрешность Δxi, тогда:
См. также
- Измерение физических величин
- Класс точности
- Метрология
- Система автоматизированного сбора данных со счетчиков по радиоканалу
- Методы электроаналитической химии
Литература
- Назаров Н. Г. Метрология. Основные понятия и математические модели. М.: Высшая школа, 2002. 348 с.
- Лабораторные занятия по физике. Учебное пособие/Гольдин Л. Л., Игошин Ф. Ф., Козел С. М. и др.; под ред. Гольдина Л. Л. — М.: Наука. Главная редакция физико-математичекой литературы, 1983. — 704 с.
Wikimedia Foundation.
2010.
1.1 Задачи теории ошибок
В
теории ошибок на основе теории вероятностей
с использованием методов математической
статистики решают следующие задачи:
-
Изучение
причин возникновения ошибок измерений,
их свойств и законов распределения их
вероятностей; -
Определение
наиболее надёжного значения искомой
величины из результатов её многократных
измерений; -
Оценка
точности непосредственно выполненных
результатов измерений и предвычисление
ожидаемой точности функций измеренных
величин; -
Установление
допусков, т.е. критериев, ограничивающих
использование результатов измерений
в заданных пределах точности.
1.2 Классификация ошибок измерений
Ошибки
измерений подразделяют на грубые,
систематические и случайные.
К
грубым
ошибкам относят ошибки, вызванные
промахами и просчётами наблюдателя,
неисправностями приборов, резким
ухудшением внешних условий и др. С целью
их обнаружения измерения выполняются
многократно (не менее двух раз). Результаты
измерений, содержащие грубые ошибки,
необходимо выявлять и исключать из
обработки.
К
систематическим
относят
ошибки, которые входят в результаты
измерений по тому или иному закону, как
функции источников возникновения
ошибок. В практике геодезических
измерений применяют следующие способы
уменьшения влияния систематических
ошибок:
-
Устанавливают
закон появления систематических ошибок,
после чего ошибки уменьшают введением
поправок в результаты измерений; -
Применяют
соответствующую методику измерений
для того, чтобы систематические ошибки
действовали не односторонне, а изменяли
знаки; -
Используют
определённую методику обработки
результатов измерений.
Случайные
ошибки являются наиболее ярким примером
случайной величины. Их закономерности
обнаруживаются только в массовом
проявлении. Случайные ошибки неизбежны
при измерениях и не могут быть исключены
из единичного измерения. Влияние их
можно лишь ослабить, повышая качество
и количество измерений, а также надлежащей
математической обработкой результатов
измерений. Причин возникновения случайных
ошибок измерений много: влияние внешних
условий, неточности изготовления и
юстировки приборов, неточности выполнения
операций наблюдателем и т.д. Очевидно,
что случайные ошибки являются результатом
суммирования большого числа независимых
элементарных ошибок. На основании
центральной предельной теоремы Ляпунова
можно считать, что случайные ошибки
измерений подчиняются нормальному
закону распределения.
В
дальнейшем условно примем, что в любых
измерениях грубые ошибки отсутствуют,
основная часть систематических ошибок
исключена из результатов, а остаточные
систематические ошибки ничтожно малы,
т.е. будем рассматривать только случайные
ошибки (,
гдехi —
результат измерений, Х —
истинное значение измеряемой величины.)
Очевидно, что
,
а.
1.3 Свойства случайных ошибок измерений
-
Случайные
ошибки по абсолютной величине с заданной
вероятностью
не должны
превышать определённого предела,
равного
(t —
коэффициент, для которого
,m —
средняя
квадратическая ошибка)); -
Положительные
и отрицательные случайные ошибки,
равные по абсолютной величине, одинаково
часто встречаются в ряде измерений; -
Среднее
арифметическое из значений случайных
ошибок при неограниченном увеличении
числа измерений имеет пределом нуль,
т.е.
|
|
Это
свойство называют свойством компенсации.
Отклонение
от нуля свидетельствует о наличии в
результатах измерений систематических
ошибок.
-
Малые
по абсолютной величине случайные ошибки
встречаются в ряде измерений чаще, чем
большие.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Погрешности измерений
Под погрешностью
измерения будем понимать совокупность
всех ошибок измерения.
Ошибки измерений
можно классифицировать на следующие
виды:
— абсолютные и
относительные,
— положительные и
отрицательные,
— постоянные и
пропорциональные,
— грубые,
— случайные и
систематические,
— прочие.
Абсолютная
ошибкаединичного результата
измерения (Аy)
определяется как разность следующих
величин:
Аy
= yi
— yист.
yi
-y,
где: yi– единичный результат измерения;yист.– истинный результат измерения;y– среднее арифметическое значение
результата измерения (далее среднее).
Постоянной
называется абсолютная ошибка,
которая не зависит от значения измеряемой
величины (y y
).
Ошибка пропорциональная,
если названная зависимость существует.
Характер ошибки измерения (постоянная
или пропорциональная) определяется
после проведения специальных исследований.
Относительная
ошибкаединичного результата
измерения (Вy)
рассчитывается как отношение следующих
величин:
.
Из этой формулы
следует, что величина относительной
ошибки зависит не только от величины
абсолютной ошибки, но и от значения
измеряемой величины. При неизменности
измеряемой величины (y)
относительную ошибку измерения можно
уменьшить только за счет снижения
величины абсолютной ошибки (Аy).
При постоянстве абсолютной ошибки
измерения для уменьшения относительной
ошибки измерения можно использовать
прием увеличения значения измеряемой
величины.
Знак ошибки
(положительный или отрицательный)
определяется разницей между единичным
и полученным (средним арифметическим)
результатом измерения:
yi-y> 0 (ошибка
положительная);
yi-y< 0 (ошибка
отрицательная).
Грубая ошибкаизмерения (промах) возникает при нарушении
методики измерения. Результат измерения,
содержащий грубую ошибку, обычно
значительно отличается по величине от
других результатов. Наличие грубых
ошибок измерения в выборке устанавливается
только методамиматематической
статистики (при числе повторений
измерения n>2).
С методами обнаружения грубых ошибок
познакомьтесь самостоятельно в [3-6].
К случайным
ошибкамотносят ошибки, которые не
имеют постоянной величины и знака. Такие
ошибки возникают под действием следующих
факторов: не известных исследователю;
известных, но нерегулируемых; постоянно
изменяющихся.
Случайные
ошибки можно оценить только после
проведения измерений.
Количественной
оценкой модуля величины случайной
ошибки измерения могут являться следующие
параметры: выборочная дисперсия
единичных значений и среднего значения;
выборочные абсолютные стандартные
отклонения единичных значений и среднего
значения; выборочные относительные
стандартные отклонения единичных
значений и среднего значения; генеральная
дисперсия единичных значений
),
соответственно, и др.
Случайные ошибки
измерения невозможно исключить, их
можно только уменьшить. Один из основных
способов уменьшения величины случайной
ошибки измерения – это увеличение числа
(объема выборки) единичных измерений
(увеличение величины n).
Объясняется это тем, что величина
случайных ошибок обратно пропорциональна
величинеn, например:
.
Систематические
ошибки– это ошибки с неизменными
величиной и знаком или изменяющиеся по
известному закону. Эти ошибки вызываются
постоянными факторами. Систематические
ошибки можно количественно оценивать,
уменьшать и даже исключать.
Систематические
ошибки классифицируют на ошибки I,IIиIIIтипов.
К систематическим
ошибкам I типаотносят ошибки известного происхождения,
которые могут быть до проведения
измерения оценены путем расчета. Эти
ошибки можно исключить, вводя их в
результат измерения в виде поправок.
Примером ошибки такого типа является
ошибка при титрометрическом определении
объемной концентрации раствора, если
титрант был приготовлен при одной
температуре, а измерение концентрации
проводилось при другой. Зная зависимость
плотности титранта от температуры,
можно до проведения измерения рассчитать
изменение объемной концентрации
титранта, связанное с изменением его
температуры, и эту разницу учесть в виде
поправки в результате измерения.
Систематическиеошибки II типа– это ошибки известного происхождения,
которые можно оценить только в ходе
эксперимента или в результате проведения
специальных исследований. К этому типу
ошибок относят инструментальные
(приборные), реактивные, эталонные и др.
ошибки. Познакомьтесь с особенностями
таких ошибок самостоятельно в [5].
Любой прибор при
его применении в процедуре измерения
вносит в результат измерения свои
приборные ошибки. При этом часть этих
ошибок случайная, а другая часть –
систематическая. Случайные ошибки
приборов отдельно не оценивают, их
оценивают в общей совокупности со всеми
другими случайными ошибками измерения.
Каждый экземпляр
любого прибора имеет свою персональную
систематическую ошибку. Для того чтобы
оценить эту ошибку, необходимо проводить
специальные исследования.
Наиболее надежный
способ оценки приборной систематической
ошибки IIтипа – это сверка
работы приборов по эталонам. Для мерной
посуды (пипетка, бюретка, цилиндры и
др.) проводят специальную процедуру –
калибровку.
На практике наиболее
часто требуется не оценить, а уменьшить
или исключить систематическую ошибку
IIтипа. Самыми распространенными
методами уменьшения систематических
ошибок являютсяметоды релятивизации
и рандомизации. Познакомьтесь с
этими методами самостоятельно в [5].
К ошибкам III
типаотносят ошибки неизвестного
происхождения. Эти ошибки можно обнаружить
только после устранения всех систематических
ошибокIиIIтипов.
К прочим ошибкамотнесем все другие виды ошибок, не
рассмотренные выше (допускаемые,
возможные предельные ошибки и др.).
Понятие возможных предельных ошибок
применяется в случаях использования
средств измерения и предполагает
максимально возможную по величине
инструментальную ошибку измерения
(реальное же значение ошибки может быть
меньше величины возможной предельной
ошибки).
При использовании
средств измерения можно рассчитать
возможную предельную абсолютную ()
или относительную ()
погрешность измерения. Так, например,
возможная предельная абсолютная
погрешность измерения находится как
сумма возможных предельных случайных
()
и неисключенных систематических ()
ошибок:
=
+
При выборках малого
объема (n20)
неизвестной генеральной совокупности,
подчиняющейся нормальному закону
распределения, случайные возможные
предельные ошибки измерений можно
оценить следующим образом:
=
=
,
где:
– доверительный интервал для
соответствующей вероятностиР;
–квантиль
распределения Стьюдента для вероятности
Ри выборки объемомn или при
числе степеней свободыf
= n – 1.
Абсолютная возможная
предельная погрешность измерения в
этом случае будет равна:
=
+
.
Если результаты
измерений не подчиняются нормальному
закону распределения, то оценка
погрешностей проводится по другим
формулам.
Определение
величины
зависит от наличия у средства
измерения класса точности. Если средство
измерения не имеет класса точности, тоза величину
можно принять минимальную цену
деления шкалы(или ее половину) средства
измерения [5]. Для средства измерения с
известным классом точности за величинуможно принять абсолютнуюдопускаемуюсистематическую ошибку средства
измерения ():
.
Величина
рассчитывается исходя из формул,
приведенных в табл. 2.
Для многих средств
измерения класс точности указывается
в виде чисел а10n, гдеаравно 1; 1,5; 2; 2,5; 4; 5; 6 иnравно 1; 0; -1; -2 и т.д., которые показывают
величину возможной предельной допускаемой
систематической ошибки (Еy,
доп.) и специальных знаков,
свидетельствующих о ее типе (относительная,
приведенная, постоянная, пропорциональная).
Если известны
составляющие абсолютной систематической
ошибки среднего арифметического
результата измерения (например, приборная
ошибка, ошибка метода и др.), то ее можно
оценить по формуле
,
где: m– число
составляющих систематическую ошибку
среднего результата измерения;
k– коэффициент,
определяемый вероятностьюРи числомm;
–абсолютная
систематическая ошибка отдельной
составляющей.
Отдельными
составляющими погрешности можно
пренебрегать при выполнении соответствующих
условий.
Таблица 2
Примеры обозначения
классов точности средств измерения
|
Обозначение точности |
Формула |
Характеристика |
|
|
в |
на |
||
|
1,5 |
1,5 |
|
Приведенная |
|
|
1 |
|
Приведенная |
|
|
0,5 |
|
Постоянная |
|
0,02/ 0,01 |
0,02/ 0,01 |
c |
Пропорциональная |
Систематическими
ошибками можно пренебрегать, если
выполняется неравенство
0,8.
В этом случае
принимают
.
Случайными ошибками
можно пренебречь при условии
8.
Для этого случая
.
Чтобы общая
погрешность измерения определялась
только систематическими ошибками,
увеличивают число повторных измерений.
Минимально необходимое для этого число
повторных измерений (nmin) можно
рассчитать только при известном значении
генеральной совокупности единичных
результатов по формуле

Оценка погрешностей
измерения зависит не только от условий
измерения, но и от типа измерения (прямое
или косвенное).
Деление измерений
на прямые и косвенные достаточно условно.
В дальнейшем под прямыми измерениямибудем понимать измерения значения
которых берут непосредственно из опытных
данных, например, считывают
со шкалы прибора (широко известный
пример прямого измерения –измерение
температуры термометром). Ккосвенным
измерениям будем относить
такие, результат которых получают на
основании известной зависимости между
искомой величиной и величинами,
определяемыми в результате прямых
измерений. При этомрезультаткосвенного измеренияполучают расчетным
путемкак значение функции,аргументами которой являются результаты
прямых измерений (x1,x2,
…,xj,.…,xk).
Необходимо знать,
что ошибки косвенных измерений всегда
больше, чем ошибки отдельных прямых
измерений.
Ошибки косвенных
измеренийоцениваются по
соответствующим законам накопления
ошибок (приk2).
Закон накопления
случайных ошибоккосвенных измерений
выглядит следующим образом:
.
Закон накопления
возможных предельных абсолютных
систематических ошибок косвенных
измерений представляется следующими
зависимостями:
;
.
Закон накопления
возможных предельных относительных
систематических ошибоккосвенных
измерений имеет следующий вид:
;
.
В случаях, когда
искомая величина (y) рассчитывается
как функция результатов нескольких
независимых прямых измерений вида,
закон накопления предельных относительных
систематических ошибок косвенных
измерений принимает более простой вид:
;
.
Ошибки и погрешности
измерений определяют их точность,
воспроизводимость и правильность.
Точностьтем
выше, чем меньше величина погрешности
измерения.
Воспроизводимостьрезультатов измерений улучшается при
уменьшении случайных ошибок измерений.
Правильность
результата измерений увеличивается
с уменьшением остаточных систематических
ошибок измерений.
Более
подробно с теорией ошибок измерений и
их особенностями познакомьтесь
самостоятельно [4,5]. Обращаю ваше внимание
на то, что современные формы представления
конечных результатов измерений
обязательно требуют приведения ошибок
или погрешностей измерения (вторичных
данных). При этом погрешности и ошибки
измерений должны представляться числами,
которые содержат не более двух
значащих цифр
[3].
Соседние файлы в папке Литература
- #
- #
- #
Погре́шность измере́ния — оценка отклонения величины измеренного значения величины от её истинного значения. Погрешность измерения является характеристикой (мерой) точности измерения.
Поскольку выяснить с абсолютной точностью истинное значение любой величины невозможно, то невозможно и указать величину отклонения измеренного значения от истинного. (Это отклонение принято называть ошибкой измерения. В ряде источников, например, в БСЭ, термины ошибка измерения и погрешность измерения используются как синонимы.) Возможно лишь оценить величину этого отклонения, например, при помощи статистических методов. При этом за истинное значение принимается среднестатистическое значение, полученное при статистической обработке результатов серии измерений. Это полученное значение не является точным, а лишь наиболее вероятным. Поэтому в измерениях необходимо указывать, какова их точность. Для этого вместе с полученным результатом указывается погрешность измерений. Например, запись T=2.8±0.1 c. означает, что истинное значение величины T лежит в интервале от 2.7 с. до 2.9 с. некоторой оговоренной вероятностью (см. доверительный интервал, доверительная вероятность, стандартная ошибка).
В 2006 году на международном уровне был принят новый документ, диктующий условия проведения измерений и установивший новые правила сличения государственных эталонов. Понятие «погрешность» стало устаревать, вместо него было введено понятие «неопределенность измерений».
Содержание
- 1 Определение погрешности
- 2 Классификация погрешностей
- 2.1 По форме представления
- 2.2 По причине возникновения
- 2.3 По характеру проявления
- 2.4 По способу измерения
- 3 См. также
- 4 Литература
Определение погрешности
В зависимости от характеристик измеряемой величины для определения погрешности измерений используют различные методы.
- Метод Корнфельда, заключается в выборе доверительного интервала в пределах от минимального до максимального результата измерений, и погрешность как половина разности между максимальным и минимальным результатом измерения:
- Средняя квадратическая погрешность:
- Средняя квадратическая погрешность среднего арифметического:
Классификация погрешностей
По форме представления
- Абсолютная погрешность — ΔX является оценкой абсолютной ошибки измерения. Величина этой погрешности зависит от способа её вычисления, который, в свою очередь, определяется распределением случайной величины Xmeas. При этом равенство:
ΔX = | Xtrue − Xmeas | ,
где Xtrue — истинное значение, а Xmeas — измеренное значение, должно выполняться с некоторой вероятностью близкой к 1. Если случайная величина Xmeas распределена по нормальному закону, то, обычно, за абсолютную погрешность принимают её среднеквадратичное отклонение. Абсолютная погрешность измеряется в тех же единицах измерения, что и сама величина.
- Относительная погрешность — отношение абсолютной погрешности к тому значению, которое принимается за истинное:

Относительная погрешность является безразмерной величиной, либо измеряется в процентах.
- Приведенная погрешность — относительная погрешность, выраженная отношением абсолютной погрешности средства измерений к условно принятому значению величины, постоянному во всем диапазоне измерений или в части диапазона. Вычисляется по формуле
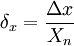
где Xn — нормирующее значение, которое зависит от типа шкалы измерительного прибора и определяется по его градуировке:
— если шкала прибора односторонняя, т.е. нижний предел измерений равен нулю, то Xn определяется равным верхнему пределу измерений;
— если шкала прибора двухсторонняя, то нормирующее значение равно ширине диапазона измерений прибора.
Приведенная погрешность — безразмерная величина (может измеряться в процентах).
По причине возникновения
- Инструментальные / приборные погрешности — погрешности, которые определяются погрешностями применяемых средств измерений и вызываются несовершенством принципа действия, неточностью градуировки шкалы, ненаглядностью прибора.
- Методические погрешности — погрешности, обусловленные несовершенством метода, а также упрощениями, положенными в основу методики.
- Субъективные / операторные / личные погрешности — погрешности, обусловленные степенью внимательности, сосредоточенности, подготовленности и другими качествами оператора.
В технике применяют приборы для измерения лишь с определенной заранее заданной точностью – основной погрешностью, допускаемой нормали в нормальных условиях эксплуатации для данного прибора.
Если прибор работает в условиях, отличных от нормальных, то возникает дополнительная погрешность, увеличивающая общую погрешность прибора. К дополнительным погрешностям относятся: температурная, вызванная отклонением температуры окружающей среды от нормальной, установочная, обусловленная отклонением положения прибора от нормального рабочего положения, и т.п. За нормальную температуру окружающего воздуха принимают 20°С, за нормальное атмосферное давление 01,325 кПа.
Обобщенной характеристикой средств измерения является класс точности, определяемый предельными значениями допускаемых основной и дополнительной погрешностей, а также другими параметрами, влияющими на точность средств измерения; значение параметров установлено стандартами на отдельные виды средств измерений. Класс точности средств измерений характеризует их точностные свойства, но не является непосредственным показателем точности измерений, выполняемых с помощью этих средств, так как точность зависит также от метода измерений и условий их выполнения. Измерительным приборам, пределы допускаемой основной погрешности которых заданы в виде приведенных основных (относительных) погрешностей, присваивают классы точности, выбираемые из ряда следующих чисел: (1; 1,5; 2,0; 2,5; 3,0; 4,0; 5,0; 6,0)*10n, где n = 1; 0; -1; -2 и т.д.
По характеру проявления
- Случайная погрешность — погрешность, меняющаяся (по величине и по знаку) от измерения к измерению. Случайные погрешности могут быть связаны с несовершенством приборов (трение в механических приборах и т.п.), тряской в городских условиях, с несовершенством объекта измерений (например, при измерении диаметра тонкой проволоки, которая может иметь не совсем круглое сечение в результате несовершенства процесса изготовления), с особенностями самой измеряемой величины (например при измерении количества элементарных частиц, проходящих в минуту через счётчик Гейгера).
- Систематическая погрешность — погрешность, изменяющаяся во времени по определенному закону (частным случаем является постоянная погрешность, не изменяющаяся с течением времени). Систематические погрешности могут быть связаны с ошибками приборов (неправильная шкала, калибровка и т.п.), неучтёнными экспериментатором.
- Прогрессирующая (дрейфовая) погрешность — непредсказуемая погрешность, медленно меняющаяся во времени. Она представляет собой нестационарный случайный процесс.
- Грубая погрешность (промах) — погрешность, возникшая вследствие недосмотра экспериментатора или неисправности аппаратуры (например, если экспериментатор неправильно прочёл номер деления на шкале прибора, если произошло замыкание в электрической цепи).
По способу измерения
- Погрешность прямых измерений
- Погрешность косвенных измерений — погрешность вычисляемой (не измеряемой непосредственно) величины:
Если F = F(x1,x2…xn), где xi — непосредственно измеряемые независимые величины, имеющие погрешность Δxi, тогда:
См. также
- Измерение физических величин
- Класс точности
- Метрология
- Система автоматизированного сбора данных со счетчиков по радиоканалу
- Методы электроаналитической химии
Литература
- Назаров Н. Г. Метрология. Основные понятия и математические модели. М.: Высшая школа, 2002. 348 с.
- Лабораторные занятия по физике. Учебное пособие/Гольдин Л. Л., Игошин Ф. Ф., Козел С. М. и др.; под ред. Гольдина Л. Л. — М.: Наука. Главная редакция физико-математичекой литературы, 1983. — 704 с.
Wikimedia Foundation.
2010.
На чтение 9 мин Просмотров 1.6к. Опубликовано 03.10.2021
Теория ошибок измерений изучает свойства ошибок и законы их распределения, методы обработки измерений с учетом их ошибок, а также способы вычисления числовых характеристик точности измерений. При многократных измерениях одной и той же величины результаты измерений получаются неодинаковыми. Этот очевидный факт говорит о том, что измерения сопровождаются разными по величине и по знаку ошибками. Задача теории ошибок – нахождение наиболее надежного значения измеренной величины, оценка точности результатов измерений и их функций и установление допусков, ограничивающих использование результатов обработки измерений.
По своей природе ошибки бывают грубые, систематические и случайные.
Грубые ошибки являются результатом промахов и просчетов. Их можно избежать при внимательном и аккуратном отношении к работе и организации надежного полевого контроля измерений. В теории ошибок грубые ошибки не изучаются.
Систематические ошибки имеют определенный источник, направление и величину. Если источник систематической ошибки обнаружен и изучен, то можно получить формулу влияния этой ошибки на результат измерения и затем ввести в него поправку; это исключит влияние систематической ошибки. Пока источник какой-либо систематической ошибки не найден, приходится считать ее случайной ошибкой, ухудшающей качество измерений.
Случайные ошибки измерений обусловлены точностью способа измерений (строгостью теории), точностью измерительного прибора, квалификацией исполнителя и влиянием внешних условий. Закономерности случайных ошибок проявляются в массе, то-есть, при большом количестве измерений; такие закономерности называют статистическими. Освободить результат единичного измерения от случайных ошибок невозможно; невозможно также предсказать случайную ошибку единичного измерения. Теория ошибок занимается в основном изучением случайных ошибок.
Случайная истинная ошибка измерения Δ – это разность между измеренным значением величины l и ее истинным значением X:
(1.25)
Свойства случайных ошибок. Случайные ошибки подчиняются некоторым закономерностям:
1. при данных условиях измерений абсолютные значения случайных ошибок не превосходят некоторого предела; если какая-либо ошибка выходит за этот предел, она считается грубой,
2. положительные и отрицательные случайные ошибки равновозможны,
3. среднее арифметическое случайных ошибок стремится к нулю при неограниченном возрастании числа измерений. Третье свойство случайных ошибок записывается так:
(1.26)
4. малые по абсолютной величине случайные ошибки встречаются чаще, чем большие.
Кроме того, во всей массе случайных ошибок не должно быть явных закономерностей ни по знаку, ни по величине. Если закономерность обнаруживается, значит здесь сказывается влияние какой-то систематической ошибки.
Средняя квадратическая ошибка одного измерения. Для оценки точности измерений можно применять разные критерии; в геодезии таким критерием является средняя квадратическая ошибка. Это понятие было введено Гауссом; он же разработал основные положения теории ошибок. Средняя квадратическая ошибка одного измерения обозначается буквой m и вычисляется по формуле Гаусса:
(1.27)
где: ;
n – количество измерений одной величины.
Средняя квадратическая ошибка очень чувствительна к большим по абсолютной величине ошибкам, так как каждая ошибка возводится в квадрат. В то же время она является устойчивым критерием для оценки точности даже при небольшом количество измерений; начиная с некоторого n дальнейшее увеличение числа измерений почти не изменяет значения m; доказано, что уже при n = 8 значение m получается достаточно надежным.
Предельная ошибка ряда измерений обозначается Δпред; она обычно принимается равной 3*m при теоретических исследованиях и 2*m или 2.5*m при практических измерениях. Считается, что из тысячи измерений только три ошибки могут достигать или немного превосходить значение Δпред = 3*m.
Отношение mx/X называется средней квадратической относительной ошибкой; для некоторых видов измерений относительная ошибка более наглядна, чем m. Относительная ошибка выражается дробью с числителем, равным 1, например, mx/X = 1/10 000.
Средняя квадратическая ошибка функции измеренных величин. Выведем формулу средней квадратической ошибки функции нескольких аргументов произвольного вида:
F = f( X, Y, Z … ), (1.28)
здесь: X, Y, Z … – истинные значения аргументов,
F – истинное значение функции.
В результате измерений получены измеренные значения аргументов lX, lY, lZ, при этом:

где ΔX, ΔY, ΔZ – случайные истинные ошибки измерения аргументов.
Функцию F можно выразить через измеренные значения аргуметов и их истинные ошибки:
Разложим функцию F в ряд Тейлора, ограничившись первой степенью малых приращений ΔX, ΔY, ΔZ:
(1.30)
Разность является случайной истинной ошибкой функции с противоположным знаком, поэтому:
(1.31)
Если выполнить n измерений аргументов X, Y, Z, то можно записать n уравнений вида (1.31). Возведем все эти уравнения в квадрат и сложим их; суммарное уравнение разделим на n и получим
В силу третьего свойства случайных ошибок члены, содержащие произведения случайных ошибок, будут незначительными по величине, и их можно не учитывать; таким образом,
(1.32)
Как частные случаи формулы (1.32) можно написать выражения для средней квадратической ошибки некоторых функций:
Если функция имеет вид произведения нескольких аргументов,
F = x * y * z,
то для нее можно записать выражение относительной ошибки функции:
(1.33)
которое в некоторых случаях оказывается более удобным, чем формула (1.32).
Принцип равных влияний. В геодезии часто приходится определять средние квадратические ошибки аргументов по заданной средней квадратической ошибке функции. Если аргумент всего один, то решение задачи не представляет трудности. Если число аргументов t больше одного, то возникает задача нахождения t неизвестных из одного уравнения, которую можно решить, применяя принцип равных влияний. Согласно этому принципу все слагаемые правой части формулы (1.32) или (1.33) считаются равными между собой.
Арифметическая середина. Пусть имеется n измерений одной величины X, то-есть,

Сложим эти равенства, суммарное уравнение разделим на n и получим:
(1.35)
Величина (1.36)
называется средним арифметическим или простой арифметической серединой. Запишем (1.35) в виде
по третьему свойству ошибок (1.26) можно написать:
что означает, что при неограниченном возрастании количества измерений простая арифметическая середина стремится к истинному значению измеряемой величины. При ограниченном количестве измерений арифметическая середина является наиболее надежным и достоверным значением измеряемой величины.
Запишем формулу (1.36) в виде
и подсчитаем среднюю квадратическую ошибку арифметической середины, которая обозначается буквой M. Согласно формуле (1.32) напишем:
или
Но ml1 = ml2 = … = mln= m по условию задачи, так как величина X измеряется при одних и тех же условиях. Тогда в квадратных скобках будет n * m2, одно n сократится и в итоге получим:
M2 = m2/n
или
(1.37)
то-есть, средняя квадратическая ошибка арифметической середины в корень из n раз меньше ошибки одного измерения.
Вычисление средней квадратической ошибки по уклонениям от арифметической середины. Формулу Гаусса (1.27) применяют лишь в теоретических выкладках и при исследованиях приборов и методов измерений, когда известно истинное значение измеряемой величины. На практике оно, как правило, неизвестно, и оценку точности выполняют по уклонениям от арифметической середины.
Пусть имеется ряд равноточных измерений величины X:
l1, l2 , …, ln .
Вычислим арифметическую середину X0 = [1]/n и образуем разности:

Сложим все разности и получим [l] – n * X0 = [V]. По определению арифметической середины n * X0 = [l], поэтому:
[V] = 0. (1.39)
Величины V называют вероятнейшими ошибками измерений; именно по их значениям и вычисляют на практике среднюю квадратическую ошибку одного измерения, используя для этого формулу Бесселя:
(1.40)
Приведем вывод этой формулы. Образуем разности случайных истинных ошибок измерений Δ и вероятнейших ошибок V:

Разность (X0 – X) равна истинной ошибке арифметической середины; обозначим ее Δ0 и перепишем уравнения (1.41):

Возведем все уравнения (1.42) в квадрат, сложим их и получим:
.
Второе слагаемое в правой части этого выражения равно нулю по свойству (1.39), следовательно,
.
Разделим это уравнение на n и учтя, что [Δ2]/n =m2, получим:
(1.43)
Заменим истинную ошибку арифметической середины Δ0 ее средней квадратической ошибкой ; такая замена практически не изменит правой части формулы (1.43). Итак,
,
откуда ;
после перенесения (n-1) в правую часть и извлечения квадратного корня получается формула Бесселя (1.40).
Для вычисления средней квадратической ошибки арифметической середины на основании (1.37) получается формула:
(1.44)
Веса измерений. Измерения бывают равноточные и неравноточные. Например, один и тот же угол можно измерить точным или техническим теодолитом, и результаты таких измерений будут неравноточными. Или один и тот же угол можно измерить разным количеством приемов; результаты тоже будут неравноточными. Понятно, что средние квадратические ошибки неравноточных измерений будут неодинаковы. Из опыта известно, что измерение, выполненное с большей точностью (с меньшей ошибкой), заслуживает большего доверия.
Вес измерения – это условное число, характеризующее надежность измерения, степень его доверия; вес обозначается буквой p. Значение веса измерения получают по формуле:
p = C/m2 (1.45)
где C – в общем случае произвольное положительное число.
При неравноточных измерениях одной величины наиболее надежное ее значение получают по формуле средневесовой арифметической середины:
(1.46)
или X0 = [l*p] / [p] .
Ошибку измерения, вес которого равен 1, называют средней квадратической ошибкой единицы веса; она обозначается буквой m. Из формулы (1.45) получаем
откуда (1.47)
то-есть, за число C принимают квадрат ошибки единицы веса.
Подсчитаем вес P средневесовой арифметической середины. По определению веса имеем:
(1.48)
Согласно (1.46) и (1.32) напишем:
Подставим сюда вместо mli2 их выражения через вес m2 = C/p , тогда:
Подставим это выражение в формулу (1.48) и получим,
P = [p], (1.49)
то-есть, вес средневесовой арифметической середины равен сумме весов отдельных измерений.
В случае равноточных измерений, когда веса всех измерений одинаковы и равны единице, формула (1.49) принимает вид:
P = n. (1.50)
При обработке больших групп измерений (при уравнивании геодезических построений по МНК) вычисляются значение ошибки единицы веса, веса измерений и других элементов после уравнивания, а ошибка любого уравненного элемента подсчитывается по формуле:
(1.51)
где pi – вес i-того элемента.


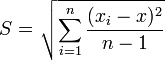
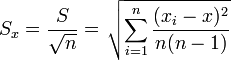
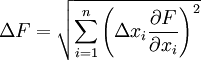
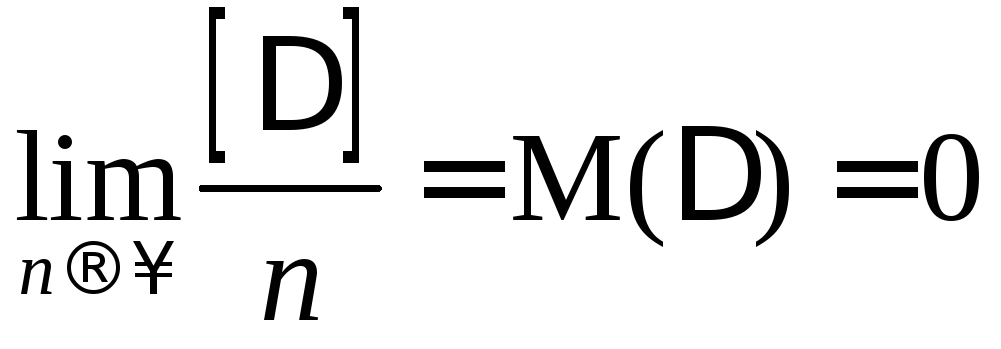

 1
1 0,5
0,5