Выборочная оценка всегда ошибочна. Так, стандартная ошибка средней показывает разброс средней. Для бинарной переменной (с двумя возможными значениями) средней арифметической является доля «успехов». В этой статье показано, как рассчитать дисперсию и стандартную ошибку доли.
Долю используют в качестве выборочной оценки вероятности. Обозначим долю как p*, а истинную вероятность как p . При бесконечно большом количестве наблюдений доля p* стремится к теоретической вероятности p. Этот факт известен со времен Якоба Бернулли.
Дисперсия и стандартная ошибка доли
Обратимся вначале к дисперсии биномиальной переменной. Если истинная вероятность p не известна, то используют ее оценку p*.
где B – сумма «успехов» в выборке;
n – количество наблюдений;
p* – оценка вероятности, т.е. доля «успехов».
Нас интересует дисперсия величины B/n. Согласно одному из свойств дисперсии, постоянный множитель выносится за скобки и возводится в квадрат.
Получаем формулу дисперсию доли:
Почти полная аналогия со средней арифметической. В числителе дисперсия самой переменной (1 или 0), внизу – объем выборки.
Стандартная ошибка доли – корень из дисперсии:
Стандартная ошибка доли при увеличении выборки ведет себя так же, как и стандартная ошибка средней: чем больше выборка, тем меньше ошибка, но при этом уменьшение постоянно замедляется.
Как известно, максимально возможная дисперсия переменной в схеме Бернулли достигается при p*=0,5. Она равна 0,5*(1-0,5)=0,25. Отсюда легко рассчитать максимальную стандартную ошибку доли, полученную по некоторой выборке.
Изобразим эту зависимость на диаграмме.
График имеет знакомую конфигурацию: ошибка уменьшается с замедлением. Так, при объеме выборки равной 100 наблюдениям стандартная ошибка (максимально возможная!) равна 0,05 (или 5 процентных пункта). При n=1000 стандартная ошибка доли составляет всего 0,0158 (или 1,58 процентных пункта). Повторюсь, что это максимум. Именно поэтому опросы общественно мнения редко превышают 1500-2000 человек (чтобы еще была возможность разбить данные на группы достаточно размера).
На практике довольно часто приходится анализировать бинарные данные. Это может быть анкетирование покупателей, контроль качества продукции и много чего еще. Поэтому доля, как оценка вероятности наступления интересующего события, – довольно распространенный показатель. Дисперсия и стандартная ошибка доли используется в расчете приблизительных доверительных интервалов вероятности и в проверке статистических гипотез.
Поделиться в социальных сетях:
Выборочная оценка всегда ошибочна. Так, стандартная ошибка средней показывает разброс средней. Для бинарной переменной (с двумя возможными значениями) средней арифметической является доля «успехов». В этой статье показано, как рассчитать дисперсию и стандартную ошибку доли.
Долю используют в качестве выборочной оценки вероятности. Обозначим долю как p*, а истинную вероятность как p . При бесконечно большом количестве наблюдений доля p* стремится к теоретической вероятности p. Этот факт известен со времен Якоба Бернулли.
Дисперсия и стандартная ошибка доли
Обратимся вначале к дисперсии биномиальной переменной. Если истинная вероятность p не известна, то используют ее оценку p*.
где B – сумма «успехов» в выборке;
n – количество наблюдений;
p* – оценка вероятности, т.е. доля «успехов».
Нас интересует дисперсия величины B/n. Согласно одному из свойств дисперсии, постоянный множитель выносится за скобки и возводится в квадрат.
Получаем формулу дисперсию доли:
Почти полная аналогия со средней арифметической. В числителе дисперсия самой переменной (1 или 0), внизу – объем выборки.
Стандартная ошибка доли – корень из дисперсии:
Стандартная ошибка доли при увеличении выборки ведет себя так же, как и стандартная ошибка средней: чем больше выборка, тем меньше ошибка, но при этом уменьшение постоянно замедляется.
Как известно, максимально возможная дисперсия переменной в схеме Бернулли достигается при p*=0,5. Она равна 0,5*(1-0,5)=0,25. Отсюда легко рассчитать максимальную стандартную ошибку доли, полученную по некоторой выборке.
Изобразим эту зависимость на диаграмме.
График имеет знакомую конфигурацию: ошибка уменьшается с замедлением. Так, при объеме выборки равной 100 наблюдениям стандартная ошибка (максимально возможная!) равна 0,05 (или 5 процентных пункта). При n=1000 стандартная ошибка доли составляет всего 0,0158 (или 1,58 процентных пункта). Повторюсь, что это максимум. Именно поэтому опросы общественно мнения редко превышают 1500-2000 человек (чтобы еще была возможность разбить данные на группы достаточно размера).
На практике довольно часто приходится анализировать бинарные данные. Это может быть анкетирование покупателей, контроль качества продукции и много чего еще. Поэтому доля, как оценка вероятности наступления интересующего события, – довольно распространенный показатель. Дисперсия и стандартная ошибка доли используется в расчете приблизительных доверительных интервалов вероятности и в проверке статистических гипотез.
Поделиться в социальных сетях:
Точность оценки долей
Если бы в наших руках были данные по
всем членам совокупности, то не было бы
никаких проблем связанных с точностью
оценок. Однако нам всегда приходится
довольствоваться ограниченной выборкой.
Поэтому возникает вопрос, насколько
точно доли в выборке соответствуют
долям в совокупности.
Рис. 5.4. А. Из совокупности марсиан, среди
которых 150 зеленых и 50 розовых, извлекли
случайную выборку из 10 особей. В выборку
попало 5 зеленых и 5 розовых марсиан, на
рисунке они помечены черным. Б. В таком
виде данные предстанут перед исследователем,
который не может наблюдать всю совокупность
и вынужден судить о ней по выборке.
Оценка доли розовых марсиан p = 5/10 = 0,5.
Как любая выборочная оценка, оценка
доли (обозначим ее p^) отражает
долю р в совокупности, но отклоняется
от нее в силу случайности. Рассмотрим
теперь не совокупность марсиан, а
совокупность всех значений p^ ,
вычисленных по выборкам объемом 10
каждая. (Из совокупности в 200 членов
можно получить более 106 таких
выборок). По аналогии со стандартной
ошибкой среднего найдем стандартную
ошибку доли. Для этого нужно
охарактеризовать разброс выборочных
оценок доли, то есть рассчитать стандартное
отклонение совокупности p^.
где σ p^ — стандартная ошибка
доли, σ — стандартное отклонение, n —
объем выборки.
Заменив в приведенной формуле истинное
значение доли ее оценкой p^ ,
получим оценку стандартной ошибки доли:
Из центральной предельной теоремы
вытекает, что при достаточно большом
объеме выборки выборочная оценка p^
приближенно подчиняется
нормальному распределению, имеющему
среднее р и стандартное отклонение σˆp
. Однако при значениях р, близких к 0 или
1, и при малом объеме выборки это не так.
При какой численности выборки можно
пользоваться приведенным способом
оценки? Математическая статистика
утверждает, что нормальное распределение
служит хорошим приближением, если np^
и n(1-p^)
превосходят 5. Напомним, что примерно
95% всех членов нормально распределенной
совокупности находятся в пределах двух
стандартных отклонений от среднего.
Поэтому если перечисленные условия
соблюдены, то с вероятностью 95% можно
утверждать, что истинное значение р
лежит в пределах np^
и n(1-p^).
Вернемся на минуту к сравнению операционной
летальности при галотановой и морфиновой
анестезии. Напомним, что при использовании
галотана летальность составила 13,1%
(численность группы — 61 больной), а при
использовании морфина —
14,9% (численность группы — 67 больных).
Стандартная ошибка доли для группы
Если учесть, что различие в летальности
составило лишь 2%, то маловероятно, чтобы
оно было обусловлено чем-нибудь, кроме
случайного характера выборки.
Перечислим те предпосылки, на которых
основан излагаемый подход. Мы изучаем
то, что в статистике принято называть
независимыми испытаниями Бернулли.
Эти испытания обладают следующими
свойствами.
• Каждое отдельное испытание имеет
ровно два возможных взаимно исключающих
исхода.
• Вероятность данного исхода одна и та
же в любом испытании.
• Все испытания независимы друг от
друга.
21
Соседние файлы в папке Старый материал
- #
- #
- #
- #
- #
- #
- #
Выборочная оценка всегда ошибочна. Так, стандартная ошибка средней показывает разброс средней. Для бинарной переменной (с двумя возможными значениями) средней арифметической является доля «успехов». В этой статье показано, как рассчитать дисперсию и стандартную ошибку доли.
Долю используют в качестве выборочной оценки вероятности. Обозначим долю как p*, а истинную вероятность как p . При бесконечно большом количестве наблюдений доля p* стремится к теоретической вероятности p. Этот факт известен со времен Якоба Бернулли.
Дисперсия и стандартная ошибка доли
Обратимся вначале к дисперсии биномиальной переменной. Если истинная вероятность p не известна, то используют ее оценку p*.
где B – сумма «успехов» в выборке;
n – количество наблюдений;
p* – оценка вероятности, т.е. доля «успехов».
Нас интересует дисперсия величины B/n. Согласно одному из свойств дисперсии, постоянный множитель выносится за скобки и возводится в квадрат.
Получаем формулу дисперсию доли:
Почти полная аналогия со средней арифметической. В числителе дисперсия самой переменной (1 или 0), внизу – объем выборки.
Стандартная ошибка доли – корень из дисперсии:
Стандартная ошибка доли при увеличении выборки ведет себя так же, как и стандартная ошибка средней: чем больше выборка, тем меньше ошибка, но при этом уменьшение постоянно замедляется.
Как известно, максимально возможная дисперсия переменной в схеме Бернулли достигается при p*=0,5. Она равна 0,5*(1-0,5)=0,25. Отсюда легко рассчитать максимальную стандартную ошибку доли, полученную по некоторой выборке.
Изобразим эту зависимость на диаграмме.
График имеет знакомую конфигурацию: ошибка уменьшается с замедлением. Так, при объеме выборки равной 100 наблюдениям стандартная ошибка (максимально возможная!) равна 0,05 (или 5 процентных пункта). При n=1000 стандартная ошибка доли составляет всего 0,0158 (или 1,58 процентных пункта). Повторюсь, что это максимум. Именно поэтому опросы общественно мнения редко превышают 1500-2000 человек (чтобы еще была возможность разбить данные на группы достаточно размера).
На практике довольно часто приходится анализировать бинарные данные. Это может быть анкетирование покупателей, контроль качества продукции и много чего еще. Поэтому доля, как оценка вероятности наступления интересующего события, – довольно распространенный показатель. Дисперсия и стандартная ошибка доли используется в расчете приблизительных доверительных интервалов вероятности и в проверке статистических гипотез.
Поделиться в социальных сетях:
Точность оценки долей
Если бы в наших руках были данные по
всем членам совокупности, то не было бы
никаких проблем связанных с точностью
оценок. Однако нам всегда приходится
довольствоваться ограниченной выборкой.
Поэтому возникает вопрос, насколько
точно доли в выборке соответствуют
долям в совокупности.
Рис. 5.4. А. Из совокупности марсиан, среди
которых 150 зеленых и 50 розовых, извлекли
случайную выборку из 10 особей. В выборку
попало 5 зеленых и 5 розовых марсиан, на
рисунке они помечены черным. Б. В таком
виде данные предстанут перед исследователем,
который не может наблюдать всю совокупность
и вынужден судить о ней по выборке.
Оценка доли розовых марсиан p = 5/10 = 0,5.
Как любая выборочная оценка, оценка
доли (обозначим ее p^) отражает
долю р в совокупности, но отклоняется
от нее в силу случайности. Рассмотрим
теперь не совокупность марсиан, а
совокупность всех значений p^ ,
вычисленных по выборкам объемом 10
каждая. (Из совокупности в 200 членов
можно получить более 106 таких
выборок). По аналогии со стандартной
ошибкой среднего найдем стандартную
ошибку доли. Для этого нужно
охарактеризовать разброс выборочных
оценок доли, то есть рассчитать стандартное
отклонение совокупности p^.
где σ p^ — стандартная ошибка
доли, σ — стандартное отклонение, n —
объем выборки.
Заменив в приведенной формуле истинное
значение доли ее оценкой p^ ,
получим оценку стандартной ошибки доли:
Из центральной предельной теоремы
вытекает, что при достаточно большом
объеме выборки выборочная оценка p^
приближенно подчиняется
нормальному распределению, имеющему
среднее р и стандартное отклонение σˆp
. Однако при значениях р, близких к 0 или
1, и при малом объеме выборки это не так.
При какой численности выборки можно
пользоваться приведенным способом
оценки? Математическая статистика
утверждает, что нормальное распределение
служит хорошим приближением, если np^
и n(1-p^)
превосходят 5. Напомним, что примерно
95% всех членов нормально распределенной
совокупности находятся в пределах двух
стандартных отклонений от среднего.
Поэтому если перечисленные условия
соблюдены, то с вероятностью 95% можно
утверждать, что истинное значение р
лежит в пределах np^
и n(1-p^).
Вернемся на минуту к сравнению операционной
летальности при галотановой и морфиновой
анестезии. Напомним, что при использовании
галотана летальность составила 13,1%
(численность группы — 61 больной), а при
использовании морфина —
14,9% (численность группы — 67 больных).
Стандартная ошибка доли для группы
Если учесть, что различие в летальности
составило лишь 2%, то маловероятно, чтобы
оно было обусловлено чем-нибудь, кроме
случайного характера выборки.
Перечислим те предпосылки, на которых
основан излагаемый подход. Мы изучаем
то, что в статистике принято называть
независимыми испытаниями Бернулли.
Эти испытания обладают следующими
свойствами.
• Каждое отдельное испытание имеет
ровно два возможных взаимно исключающих
исхода.
• Вероятность данного исхода одна и та
же в любом испытании.
• Все испытания независимы друг от
друга.
21
Соседние файлы в папке Старый материал
- #
- #
- #
- #
- #
- #
- #
Стандартная ошибка пропорции: формула и пример
17 авг. 2022 г.
читать 1 мин
Часто в статистике нас интересует оценка доли людей в популяции с определенной характеристикой.
Например, нас может заинтересовать оценка доли жителей определенного города, поддерживающих новый закон.
Вместо того, чтобы ходить и спрашивать каждого жителя, поддерживают ли они закон, мы вместо этого собираем простую случайную выборку и выясняем, сколько жителей в выборке поддерживают закон.
Затем мы рассчитали бы долю выборки (p̂) как:
Пример формулы пропорции:
р̂ = х / п
куда:
- x: количество лиц в выборке с определенной характеристикой.
- n: общее количество лиц в выборке.
Затем мы использовали бы эту пропорцию выборки для оценки доли населения. Например, если 47 из 300 жителей выборки поддержали новый закон, то выборочная доля будет рассчитана как 47/300 = 0,157 .
Это означает, что наша наилучшая оценка доли жителей в населении, поддержавших закон, будет равна 0,157 .
Однако нет никакой гарантии, что эта оценка будет точно соответствовать истинной доле населения, поэтому мы обычно также рассчитываем стандартную ошибку доли .
Это рассчитывается как:
Стандартная ошибка формулы пропорции:
Стандартная ошибка = √ p̂(1-p̂) / n
Например, если p̂ = 0,157 и n = 300, то мы рассчитали бы стандартную ошибку пропорции как:
Стандартная ошибка пропорции = √ 0,157 (1-0,157) / 300 = 0,021
Затем мы обычно используем эту стандартную ошибку для расчета доверительного интервала для истинной доли жителей, поддерживающих закон.
Это рассчитывается как:
Доверительный интервал для формулы доли населения:
Доверительный интервал = p̂ +/- z * √ p̂(1-p̂) / n
Глядя на эту формулу, легко увидеть, что чем больше стандартная ошибка пропорции, тем шире доверительный интервал .
Обратите внимание, что z в формуле — это z-значение, которое соответствует популярным вариантам выбора уровня достоверности:
| Уровень достоверности | z-значение | | — | — | | 0,90 | 1,645 | | 0,95 | 1,96 | | 0,99 | 2,58 |
Например, вот как рассчитать 95% доверительный интервал для истинной доли жителей города, поддерживающих новый закон:
- 95% ДИ = p̂ +/- z * √ p̂(1-p̂) / n
- 95% ДИ = 0,157 +/- 1,96 * √ 0,157 (1-0,157) / 300
- 95% ДИ = 0,157 +/- 1,96*(0,021)
- 95% ДИ = [0,10884, 0,19816]
Таким образом, с уверенностью 95% можно сказать, что истинная доля жителей города, поддерживающих новый закон, составляет от 10,884% до 19,816%.
Дополнительные ресурсы
Стандартная ошибка калькулятора пропорций
Доверительный интервал для калькулятора пропорций
Что такое доля населения?
Стандартная ошибка пропорции: формула и пример
17 авг. 2022 г.
читать 1 мин
Часто в статистике нас интересует оценка доли людей в популяции с определенной характеристикой.
Например, нас может заинтересовать оценка доли жителей определенного города, поддерживающих новый закон.
Вместо того, чтобы ходить и спрашивать каждого жителя, поддерживают ли они закон, мы вместо этого собираем простую случайную выборку и выясняем, сколько жителей в выборке поддерживают закон.
Затем мы рассчитали бы долю выборки (p̂) как:
Пример формулы пропорции:
р̂ = х / п
куда:
- x: количество лиц в выборке с определенной характеристикой.
- n: общее количество лиц в выборке.
Затем мы использовали бы эту пропорцию выборки для оценки доли населения. Например, если 47 из 300 жителей выборки поддержали новый закон, то выборочная доля будет рассчитана как 47/300 = 0,157 .
Это означает, что наша наилучшая оценка доли жителей в населении, поддержавших закон, будет равна 0,157 .
Однако нет никакой гарантии, что эта оценка будет точно соответствовать истинной доле населения, поэтому мы обычно также рассчитываем стандартную ошибку доли .
Это рассчитывается как:
Стандартная ошибка формулы пропорции:
Стандартная ошибка = √ p̂(1-p̂) / n
Например, если p̂ = 0,157 и n = 300, то мы рассчитали бы стандартную ошибку пропорции как:
Стандартная ошибка пропорции = √ 0,157 (1-0,157) / 300 = 0,021
Затем мы обычно используем эту стандартную ошибку для расчета доверительного интервала для истинной доли жителей, поддерживающих закон.
Это рассчитывается как:
Доверительный интервал для формулы доли населения:
Доверительный интервал = p̂ +/- z * √ p̂(1-p̂) / n
Глядя на эту формулу, легко увидеть, что чем больше стандартная ошибка пропорции, тем шире доверительный интервал .
Обратите внимание, что z в формуле — это z-значение, которое соответствует популярным вариантам выбора уровня достоверности:
| Уровень достоверности | z-значение | | — | — | | 0,90 | 1,645 | | 0,95 | 1,96 | | 0,99 | 2,58 |
Например, вот как рассчитать 95% доверительный интервал для истинной доли жителей города, поддерживающих новый закон:
- 95% ДИ = p̂ +/- z * √ p̂(1-p̂) / n
- 95% ДИ = 0,157 +/- 1,96 * √ 0,157 (1-0,157) / 300
- 95% ДИ = 0,157 +/- 1,96*(0,021)
- 95% ДИ = [0,10884, 0,19816]
Таким образом, с уверенностью 95% можно сказать, что истинная доля жителей города, поддерживающих новый закон, составляет от 10,884% до 19,816%.
Дополнительные ресурсы
Стандартная ошибка калькулятора пропорций
Доверительный интервал для калькулятора пропорций
Что такое доля населения?
Калькулятор для расчета достаточного объема выборки
Калькулятор ошибки выборки для доли признака
Калькулятор ошибки выборки для среднего значения
Калькулятор значимости различий долей
Калькулятор значимости различий средних
1. Формула (даже две)
Бытует заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть объем выборки маркетингового исследования. Это отчасти так, когда объем выборки сопоставим с размером генеральной совокупности. Например, при опросах организаций (B2B).
Если речь идет об исследовании жителей городов, то не важно, Москва это или Рязань – оптимальный объем выборки будет одинаков в обоих городах. Этот принцип следует из закона больших чисел и применим, только если выборка простая случайная.
На рис.1. пример выборки 15000 человек (!) при опросе в муниципальном районе. Возможно, от численности населения взяли 10%?
Размер выборки никогда не рассчитывается как процент от генеральной совокупности!
Рис.1. Размер выборки 15000 человек, как реальный пример некомпетентности (или хуже).
В таких случаях для расчета объема выборки используется следующая формула:

где
n – объем выборки,
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня,
p – доля респондентов с наличием исследуемого признака,
q = 1 – p – доля респондентов, у которых исследуемый признак отсутствует,
∆ – предельная ошибка выборки.
Доверительный уровень – это вероятность того, что реальная доля лежит в границах полученного доверительного интервала: выборочная доля (p) ± ошибка выборки (Δ). Доверительный уровень устанавливает сам исследователь в соответствии со своими требованиями к надежности полученных результатов. Чаще всего применяются доверительные уровни, равные 0,95 или 0,99. В маркетинговых исследованиях, как правило, выбирается доверительный уровень, равный 0,95. При этом уровне коэффициент Z равен 1,96.
Значения p и q чаще всего неизвестны до проведения исследования и принимаются за 0,5. При этом значении размер ошибки выборки максимален.
Допустимая предельная ошибка выборки выбирается исследователем в зависимости от целей исследования. Считается, что для принятия бизнес-решений ошибка выборки должна быть не больше 4%. Этому значению соответствует объем выборки 500-600 респондентов. Для важных стратегических решений целесообразно минимизировать ошибку выборки.
Рассмотрим кривую зависимости ошибки выборки от ее объема (Рис.2).

Рис.2. Зависимость ошибки выборки от ее объема при 95% доверительном уровне
Как видно из диаграммы, с ростом объема выборки значение ошибки уменьшается все медленнее. Так, при объеме выборки 1500 человек предельная ошибка выборки составит ±2,5%, а при объеме 2000 человек – ±2,2%. То есть, при определенном объеме выборки дальнейшее его увеличение не дает значительного выигрыша в ее точности.
Подходы к решению проблемы:
Случай 1. Генеральная совокупность значительно больше выборки:

Случай 2. Генеральная совокупность сопоставима с объемом выборки: (см. раздел исследований B2B)

где
n – объем выборки,
N – объем генеральной совокупности,
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня,
p – доля респондентов с наличием исследуемого признака,
q = 1 – p – доля респондентов, у которых исследуемый признак отсутствует, (значения p и q обычно принимаются за 0,5, поскольку точно неизвестны до проведения исследования)
∆ – предельная ошибка выборки.
Например,
рассчитаем ошибку выборки объемом 1000 человек при 95% доверительном уровне, если генеральная совокупность значительно больше объема выборки:
Ошибка выборки = 1,96 * КОРЕНЬ(0,5*0,5/1000) = 0,031 = ±3,1%
При расчете объема выборки следует также учитывать стоимость проведения исследования. Например, при цене за 1 анкету 200 рублей стоимость опроса 1000 человек составит 200 000 рублей, а опрос 1500 человек будет стоить 300 000 рублей. Увеличение затрат в полтора раза сократит ошибку выборки всего на 0,6%, что обычно неоправданно экономически.
2. Причины «раздувать» выборку
Анализ полученных данных обычно включает в себя и анализ подвыборок, объемы которых меньше основной выборки. Поэтому ошибка для выводов по подвыборкам больше, чем ошибка по выборке в целом. Если планируется анализ подгрупп / сегментов, объем выборки должен быть увеличен (в разумных пределах).
Рис.3 демонстрирует данную ситуацию. Если для исследования авиапассажиров используется выборка численностью 500 человек, то для выводов по выборке в целом ошибка составляет 4,4%, что вполне приемлемо для принятия бизнес-решений. Но при делении выборки на подгруппы в зависимости от цели поездки, выводы по каждой подгруппе уже недостаточно точны. Если мы захотим узнать какие-либо количественные характеристики группы пассажиров, совершающих бизнес-поездку и покупавших билет самостоятельно, ошибка полученных показателей будет достаточно велика. Даже увеличение выборки до 2000 человек не обеспечит приемлемой точности выводов по этой подвыборке.

Рис.3. Проектирование объема выборки с учетом необходимости анализа подвыборок
Другой пример – анализ подгрупп потребителей услуг торгово-развлекательного центра (Рис.4).

Рис.4. Потенциальный спрос на услуги торгово-развлекательного центра
При объеме выборки в 1000 человек выводы по каждой отдельной услуге (например, социально-демографический профиль, частота пользования, средний чек и др.) будут недостаточно точными для использования в бизнес планировании. Особенно это касается наименее популярных услуг (Таблица 1).
Таблица 1. Ошибка по подвыборкам потенциальных потребителей услуг торгово-развлекательного центра при выборке 1000 чел.

Чтобы ошибка в самой малочисленной подвыборке «Ночной клуб» составила меньше 5%, объем выборки исследования должен составлять около 4000 человек. Но это будет означать 4-кратное удорожание проекта. В таких случаях возможно компромиссное решение:
- увеличение выборки до 1800 человек, что даст достаточную точность для 6 самых популярных видов услуг (от кинотеатра до парка аттракционов);
- добор 200-300 пользователей менее популярных услуг с опросом по укороченной анкете (см. Таблицу 2).
Таблица 2. Разница в ошибке выборки по подвыборкам при разных объемах выборки.

При обсуждении с исследовательским агентством точности результатов планируемого исследования рекомендуется принимать во внимание бюджет, требования к точности результатов в целом по выборке и в разрезе подгрупп. Если бюджет не позволяет получить информацию с приемлемой ошибкой, лучше пока отложить проект (или поторговаться).
КАЛЬКУЛЯТОРЫ ДЛЯ РАСЧЕТА СТАТИСТИЧЕСКИХ ПОКАЗАТЕЛЕЙ И ОПРЕДЕЛЕНИЯ ЗНАЧИМОСТИ РАЗЛИЧИЙ:
КАЛЬКУЛЯТОР ДЛЯ РАСЧЕТА
ДОСТАТОЧНОГО ОБЪЁМА ВЫБОРКИ
Доверительный уровень:
Ошибка выборки (?):
%
Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)
РЕЗУЛЬТАТ
Один из важных вопросов, на которые нужно ответить при планировании исследования, — это оптимальный объем выборки. Слишком маленькая выборка не сможет обеспечить приемлемую точность результатов опроса, а слишком большая приведет к лишним расходам.
Онлайн-калькулятор объема выборки поможет рассчитать оптимальный размер выборки, исходя из максимально приемлемого для исследователя размера ошибки выборки.
Все дальнейшие формулы и расчеты относятся только к простой случайной выборке!
Формулы для других типов выборки отличаются.
Объем выборки рассчитывается по следующим формулам
1) если объем выборки значительно меньше генеральной совокупности:

2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня. Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень. Ему соответствует значение Z = 1,96.
N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели соков и нектаров, постоянно проживающие в Москве и Московской области). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).
p – доля респондентов с наличием исследуемого признака. Например, если 20% опрошенных заинтересованы в новом продукте, то p = 0,2.
q = 1 — p – доля респондентов, у которых исследуемый признак отсутствует. Значения p и q обычно принимаются за 0,5, поскольку точно неизвестны до проведения исследования. При этом значении размер ошибки выборки максимален. В данном калькуляторе значения p и q по умолчанию равны 0,5.
Δ– предельная ошибка выборки (для доли признака), приемлемая для исследователя. Считается, что для принятия бизнес-решений ошибка выборки не должна превышать 4%.
n – объем выборки. Объем выборки – это количество людей, которые опрашиваются в исследовании.
ПРИМЕР РАСЧЕТА ОБЪЕМА ВЫБОРКИ:
Допустим, мы хотим рассчитать объем выборки, предельная ошибка которой составит 4%. Мы принимаем доверительный уровень, равный 95%. Генеральная совокупность значительно больше выборки. Тогда объем выборки составит:
n = 1,96 * 1,96 * 0,5 * 0,5 / (0,04 * 0,04) = 600,25 ≈ 600 человек
Таким образом, если мы хотим получить результаты с предельной ошибкой 4%, нам нужно опросить 600 человек.
КАЛЬКУЛЯТОР ОШИБКИ ВЫБОРКИ ДЛЯ ДОЛИ ПРИЗНАКА
Доверительный уровень:
Объём выборки (n):
Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)
Доля признака (p):
%
РЕЗУЛЬТАТ
Зная объем выборки исследования, можно рассчитать значение ошибки выборки (или, другими словами, погрешность выборки).
Если бы в ходе исследования мы могли опросить абсолютно всех интересующих нас людей, мы могли бы быть на 100% уверены в полученном результате. Но ввиду экономической нецелесообразности сплошного опроса применяют выборочный подход, когда опрашивается только часть генеральной совокупности. Выборочный метод не гарантирует 100%-й точности измерения, но, тем не менее, вероятность ошибки может быть сведена к приемлемому минимуму.
Все дальнейшие формулы и расчеты относятся только к простой случайной выборке! Формулы для других типов выборки отличаются.
Ошибка выборки для доли признака рассчитывается по следующим формулам.
1) если объем выборки значительно меньше генеральной совокупности:
(в данной формуле не используется показатель объема генеральной совокупности N)
2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня. Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень. Ему соответствует значение Z = 1,96.
N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели шоколада, постоянно проживающие в Москве). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).
n – объем выборки. Объем выборки – это количество людей, которые опрашиваются в исследовании. Существует заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть и объем выборки маркетингового исследования. Это отчасти так, когда объем выборки сопоставим с объемом генеральной совокупности. Например, при опросах организаций (B2B). Если же речь идет об исследовании жителей городов, то не важно, Москва это или Рязань – оптимальный объем выборки будет одинаков в обоих городах. Этот принцип следует из закона больших чисел и применим, только если выборка простая случайная. ВАЖНО: если предполагается сравнивать какие-то группы внутри города, например, жителей разных районов, то выборку следует рассчитывать для каждой такой группы.
p – доля респондентов с наличием исследуемого признака. Например, если 20% опрошенных заинтересованы в новом продукте, то p = 0,2.
q = 1 — p – доля респондентов, у которых исследуемый признак отсутствует. Значения p и q обычно принимаются за 0,5, поскольку точно неизвестны до проведения исследования. При этом значении размер ошибки выборки максимален.
Δ– предельная ошибка выборки.
Таким образом, зная объем выборки исследования, мы можем заранее оценить показатель ее ошибки.
А получив значение p, мы можем рассчитать доверительный интервал для доли признака: (p — ∆; p + ∆)
ПРИМЕР РАСЧЕТА ОШИБКИ ВЫБОРКИ ДЛЯ ДОЛИ ПРИЗНАКА:
Например, в ходе исследования были опрошены 1000 человек (n=1000). 20% из них заинтересовались новым продуктом (p=0,2). Рассчитаем показатель ошибки выборки по формуле 1 (выберем доверительный уровень, равный 95%):
∆ = 1,96 * КОРЕНЬ (0,2*0,8/1000) = 0,0248 = ±2,48%
Рассчитаем доверительный интервал:
(p — ∆; p + ∆) = (20% — 2,48%; 20% + 2,48%) = (17,52%; 22,48%)
Таким образом, с вероятностью 95% мы можем быть уверены, что реальная доля заинтересованных в новом продукте (среди всей генеральной совокупности) находится в пределах полученного диапазона (17,52%; 22,48%).
Если бы мы выбрали доверительный уровень, равный 99%, то для тех же значений p и n ошибка выборки была бы больше, а доверительный интервал – шире. Это логично, поскольку, если мы хотим быть более уверены в том, что наш доверительный интервал «накроет» реальное значение признака, то интервал должен быть более широким.
КАЛЬКУЛЯТОР ОШИБКИ ВЫБОРКИ ДЛЯ СРЕДНЕГО ЗНАЧЕНИЯ
Доверительный уровень:
Объём выборки (n):
Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)
Среднее значение (x̄):
Стандартное отклонение (s):
РЕЗУЛЬТАТ
Зная объем выборки исследования, можно рассчитать значение ошибки выборки (или, другими словами, погрешность выборки).
Если бы в ходе исследования мы могли опросить абсолютно всех интересующих нас людей, мы могли бы быть на 100% уверены в полученном результате. Но ввиду экономической нецелесообразности сплошного опроса применяют выборочный подход, когда опрашивается только часть генеральной совокупности. Выборочный метод не гарантирует 100%-й точности измерения, но, тем не менее, вероятность ошибки может быть сведена к приемлемому минимуму.
Все дальнейшие формулы и расчеты относятся только к простой случайной выборке! Формулы для других типов выборки отличаются.
Ошибка выборки для среднего значения рассчитывается по следующим формулам.
1) если объем выборки значительно меньше генеральной совокупности:

(в данной формуле не используется показатель объема генеральной совокупности N)
2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня. Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень. Ему соответствует значение Z = 1,96
N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели мороженого, постоянно проживающие в Москве). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).
n – объем выборки. Объем выборки – это количество людей, которые опрашиваются в исследовании. Существует заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть и объем выборки маркетингового исследования. Это отчасти так, когда объем выборки сопоставим с объемом генеральной совокупности. Например, при опросах организаций (B2B). Если же речь идет об исследовании жителей городов, то не важно, Москва это или Рязань – оптимальный объем выборки будет одинаков в обоих городах. Этот принцип следует из закона больших чисел и применим, только если выборка простая случайная. ВАЖНО: если предполагается сравнивать какие-то группы внутри города, например, жителей разных районов, то выборку следует рассчитывать для каждой такой группы.
s — выборочное стандартное отклонение измеряемого показателя. В идеале на месте этого аргумента должно быть стандартное отклонение показателя в генеральной совокупности (σ), но так как обычно оно неизвестно, используется выборочное стандартное отклонение, рассчитываемое по следующей формуле:
где, x ̅ – среднее арифметическое показателя, xi– значение i-го показателя, n – объем выборки
Δ– предельная ошибка выборки.
Зная среднее значение показателя x ̅ и ошибку ∆, мы можем рассчитать доверительный интервал для среднего значения:(x ̅ — ∆; x ̅ + ∆)
ПРИМЕР РАСЧЕТА ОШИБКИ ВЫБОРКИ ДЛЯ СРЕДНЕГО ЗНАЧЕНИЯ:
Например, в ходе исследования были опрошены 1000 человек (n=1000). Каждого из них попросили указать их примерную среднюю сумму покупки (средний чек) в известной сети магазинов. Среднее арифметическое всех ответов составило 500 руб. (x ̅=500), а стандартное отклонение составило 120 руб. (s=120). Рассчитаем показатель ошибки выборки по формуле 1 (выберем доверительный уровень, равный 95%):
∆ = 1,96 * 120 / КОРЕНЬ (1000) = 7,44
Рассчитаем доверительный интервал:
(x ̅ — ∆; x ̅ + ∆) = (500 – 7,44; 500 + 7,44) = (492,56; 507,44)
Таким образом, с вероятностью 95% мы можем быть уверены, что значение среднего чека по всей генеральной совокупности находится в границах полученного диапазона: от 492,56 руб. до 507,44 руб.
КАЛЬКУЛЯТОР ЗНАЧИМОСТИ РАЗЛИЧИЙ ДОЛЕЙ
Доверительный уровень:
| Измерение 1 | Измерение 2 | |
| Доля признака (p): | % | % |
| Объём выборки (n): |
РЕЗУЛЬТАТ
Если в прошлогоднем исследовании вашу марку вспомнили 10% респондентов, а в исследовании текущего года – 15%, не спешите открывать шампанское, пока не воспользуетесь нашим онлайн-калькулятором для оценки статистической значимости различий.
Сравнивая два разных значения, полученные на двух независимых выборках, исследователь должен убедиться, что различия статистически значимы, прежде чем делать выводы.
Как известно, выборочные исследования не обеспечивают 100%-й точности измерения (для этого пришлось бы опрашивать всю целевую аудиторию поголовно, что слишком дорого). Тем не менее, благодаря методам математической статистики, мы можем оценить точность результатов любого количественного исследования и учесть ее в выводах.
В приведенном здесь калькуляторе используется двухвыборочный z-тест для долей. Для его применения должны соблюдаться следующие условия:
- Обе выборки – простые случайные
- Выборки независимы (между значениями двух выборок нет закономерной связи)
- Генеральные совокупности значительно больше выборок
- Произведения n*p и n*(1-p), где n=размер выборки а p=доля признака, – не меньше 5.
В калькуляторе используются следующие вводные данные:
Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень.
Доля признака (p) – доля респондентов с наличием исследуемого признака. Например, если 20% опрошенных заинтересованы в новом продукте, то p = 0,2.
Объем выборки (n) – это количество людей, которые опрашиваются в исследовании.
Результат расчетов – вывод о статистической значимости или незначимости различий двух измерений.
КАЛЬКУЛЯТОР ЗНАЧИМОСТИ РАЗЛИЧИЙ СРЕДНИХ
Доверительный уровень:
| Измерение 1 | Измерение 2 | |
| Среднее значение (x̄): | ||
| Стандартное отклонение (s): | ||
| Объём выборки (n): |
РЕЗУЛЬТАТ
Допустим, выборочный опрос посетителей двух разных ТРЦ показал, что средний чек в одном из них равен 1000 рублей, а в другом – 1200 рублей. Следует ли отсюда вывод, что суммы среднего чека в двух этих ТРЦ действительно отличаются?
Сравнивая два разных значения, полученные на двух независимых выборках, исследователь должен убедиться, что различия статистически значимы, прежде чем делать выводы.
Как известно, выборочные исследования не обеспечивают 100%-й точности измерения (для этого пришлось бы опрашивать всю целевую аудиторию поголовно, что слишком дорого). Тем не менее, благодаря методам математической статистики, мы можем оценить точность результатов любого количественного исследования и учесть ее в выводах.
В приведенном здесь калькуляторе используется двухвыборочный z-тест для средних значений. Для его применения должны соблюдаться следующие условия:
- Обе выборки – простые случайные
- Выборки независимы (между значениями двух выборок нет закономерной связи)
- Генеральные совокупности значительно больше выборок
- Распределения значений в выборках близки к нормальному распределению.
В калькуляторе используются следующие вводные данные:
Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень.
Среднее значение ( ̅x) – среднее арифметическое показателя.
Стандартное отклонение (s) – выборочное стандартное отклонение измеряемого показателя. В идеале на месте этого аргумента должно быть стандартное отклонение показателя в генеральной совокупности (σ), но так как обычно оно неизвестно, используется выборочное стандартное отклонение, рассчитываемое по следующей формуле:
где, x ̅ – среднее арифметическое показателя, xi– значение i-го показателя, n – объем выборки
Объем выборки (n) – это количество людей, которые опрашиваются в исследовании.
Результат расчетов – вывод о статистической значимости или незначимости различий двух измерений.
Вы можете подписаться на уведомления о новых материалах СканМаркет
Время на прочтение
15 мин
Количество просмотров 13K
предыдущие главы
20 Смещение и разброс: Два основных источника ошибок
замечание переводчика До изменения, данная глава называлась «Систематические и случайные: Два основных источника ошибок», т. е. я использовал термины «случайной ошибки» и «систематической ошибки» для перевода bias и variance. Однако, форумчанин робот@Phaker в комментарии справедливо заметил, что в области машинного обучения в русскоязычной терминологии для данных терминов закрепляются понятия «смещение» и «разброс». Я посмотрел работы К.В. Воронцова, который заслужено является одним из авторитетов в области машинного обучения в России и ресурсы профессионального сообщества, и согласился с замечанием робот@Phaker. Несмотря на то, что с моей точки зрения, между «смещением» (bias) и «разбросом» (variance) при обучении алгоритмов и «систематической ошибкой» и «случайной ошибкой» физического эксперимента существует глубокая содержательная аналогия, кроме того они одинаково выражаются математически, все же правильно использовать устоявшиеся в данной области термины. Поэтому я переработал перевод данной и последующих глав, заменив «Систематическую и Случайные ошибки» на «Смещение и Разброс» и буду придерживаться этого подхода в дальнейшем.
Предположим, ваша тренировочная, валидационная и тестовая выборки имеют одно и то же распределение. Тогда нужно брать больше данных для обучения, это только улучшит качество работы алгоритма, верно ли это?
Несмотря на то, что получение большего количества данных не может повредить работе, к сожалению, новые данные не всегда помогают настолько, насколько можно ожидать. В некоторых случаях работа по получению дополнительных данных может оказаться пустой тратой усилий. Как принять решение — в каких случаях добавлять данные, а когда не стоит об этом беспокоиться.
В машинном обучении присутствуют два главных источника ошибок: смещение и разброс (дисперсия). Понимание того, что они из себя представляют поможет вам решить — нужно ли добавлять еще данные, так же поможет выбрать тактику по улучшению качества работы классификатора.
Предположим, вы надеетесь построить кошачий распознователь, имеющий 5% ошибок. На текущий момент ошибка вашего классификатора на тренировочной выборке 15%, на валидационной выборке 16%. В таком случае добавление тренировочных данных вряд ли поможет существенно увеличить качество. Вы должны сконцентрироваться на других изменениях системы. В действительности, добавление большего количества примеров в вашу тренировочную выборку только усложнит для вашего алгоритма получение хорошего результата на этой выборке (почему так получается будет объяснено в следующих главах).
Если доля ваших ошибок на тренировочной выборке составляет 15% (что соответствует точности 85%), но вашей целью является доля ошибок в 5% (95% точность), тогда прежде всего нужно улучшить качество работы вашего алгоритма на тренировочной выборке. Качество работы алгоритма на валидационной / тестовой выборках обычно хуже, чем качество его работы на выборке для обучения (на тренировочной выборке). Нужно понимать, что те подходы, которые привели вас к точности, не превышающей 85% на примерах, с которыми ваш алгоритм знаком, не позволят получить точность в 95% на примерах, которые этот алгоритм даже не видел.
Предположим, как указано выше, доля ошибок вашего алгоритма составляет 16% (точность составляет 84%) на валидационной выборке. Мы должны разбить ошибку в 16% на два компонента:
- Первый, доля ошибок алгоритма на тренировочной выборке. В данном примере это 15%. Мы неофициально называть его смещением (bias).
- Второй, насколько хуже алгоритм работает на валидационной (или тестовой) выборке, чем на тренировочной. В нашем примере, на 1% хуже на валидационной выборке, чем на тренировочной. Будем так же неофициально считать его разбросом (variance) алгоритма.
замечание автора В статистике присутствует более точное определение для смещения и разброса (систематической и случайной ошибок), но нас это не должно тревожить. Грубо говоря, будем считать, что смещение — это ошибка вашего алгоритма на вашей тренировочной выборке, когда вы имеете очень большую тренировочную выборку. Разброс — это насколько хуже алгоритм работает на тестовой выборке по сравнению с тренировочной при тех же настройках параметров. Если использовать среднеквадратичную ошибку, то можно записать формулы, определяющие эти две величины и доказать, что общая ошибка равна сумме смещения и разброса (сумме случайных и систематических погрешностей). Но для наших целей улучшения алгоритмов в задачах машинного обучения, достаточно неформального определения смещения и разброса.
Некоторые изменения при обучении алгоритма влияют на первый компонент ошибки — на смещение ( bias ) и улучшают выполнение алгоритма на тренировочной выборке. Некоторые изменения влияют на второй компонент — на разброс ( variance ) и помогают лучше обобщить работу алгоритма на валидационную и тестовую выборки. Для выбора наиболее эффективных изменений, которые нужно внести в систему, крайне полезно понимать, как каждый из этих двух компонентов ошибки влияет на общую ошибку системы.
замечание автора: Так же есть некоторые подходы, которые одновременно уменьшают смещение и разброс, внося существенные изменения в архитектуру системы. Но их, как правило, сложнее найти и реализовать
Для выбора наиболее эффективных изменений, которые нужно внести в систему, крайне полезно понимать, как каждый из этих двух компонентов ошибки влияет на общую ошибку системы.
Развитие интуиции в понимании, какой вклад в ошибку вносит Смещение, а какой Разброс, поможет вам эффективно выбирать пути улучшения вашего алгоритма.
21 Примеры классификации ошибок
Рассмотрим нашу задачу по классификации кошек. Идеальный классификатор (например, человек) может достичь превосходного качества выполнения этой задачи.
Предположим, что качество работы нашего алгоритма следующее:
- Ошибка на тренировочной выборке = 1%
- Ошибка на валидационной выборке = 11%
Какая проблема у этого классификатора? Применив определения из предыдущей главы, мы оценим смещение в 1% и разброс в 10% (=11% — 1%). Таким образом, у нашего алгоритма большой разброс. Классификатор имеет очень низкую ошибку на тренировочной выборке, но не может обобщить результаты обучения на валидационную выборку. Другими словами, мы имеем дело с переобучением (overfitting).
Теперь рассмотрим такую ситуацию:
- Ошибка на тренировочной выборке = 15%
- Ошибка на валидационной выборке = 16%
Тогда мы оценим смещение в 15% и разброс в 1%. Этот классификатор плохо обучился на тренировочной выборке, при этом его ошибка на валидационной выборке чуть больше, чем на тренировочной. Таким образом этот классификатор имеет большое смещение, но маленький разброс. Можно сделать вывод, что этот алгоритм недообучился (underfitting).
Еще рассмотрим такое распределение ошибок:
- Ошибка на тренировочной выборке = 15%
- Ошибка на валидационной выборке = 30%
В этом случае смещение 15% и разброс тоже 15%. У данного классификатора высокие и смещение и разброс: он плохо работает на тренировочной выборке, имея высокое смещение, и его качество на валидационной выборке намного хуже, чем на тренировочной, т.е. разброс тоже велик. Данный случай трудно описать в терминах переобучения/недообучения, этот классификатор одновременно и переобучился и недообучился.
И наконец рассмотрим такую ситуацию:
- Ошибка на тренировочной выборке = 0.5%
- Ошибка на валидационной выборке = 1%
Это отлично работающий классификатор, у него низкие и смещение и разброс. Поздравим инженеров с достижением прекрасного результата!
22 Сравнение с оптимальной долей ошибок
В нашем примере по распознаванию кошек, идеальной долей ошибок является уровень, доступный «оптимальному» классификатору и этот уровень близок к 0%. Человек, рассматривающий картинку почти всегда способен распознать, присутствует ли на картинке кошка или нет и мы можем надеяться, что рано или поздно машина будет делать это так же хорошо.
Но есть и более сложные задачи. Например, представьте, что вы разрабатываете систему распознавания речи, и обнаружили, что 14% аудио записей имеют столько фонового шума или настолько неразборчивую речь, что даже человек не может разобрать, что там было сказано. В этом случае даже самая «оптимальная» система распознавания речи может иметь ошибку в районе 14%.
Допустим в приведенной задаче по распознаванию речи наш алгоритм достиг следующих результатов:
- Ошибка на тренировочной выборке = 15%
- Ошибка на валидационной выборке = 30%
Качество работы классификатора на тренировочной выборке уже близко к оптимальному, имеющему долю ошибок в 14%. Таким образом, в данном случае у нас не так много возможностей для уменьшения смещения (улучшения работы алгоритма на тренировочной выборке). Однако, не получается обобщить работу этого алгоритма на валидационную выборку, поэтому есть большое поле для деятельности по уменьшению разброса.
Этот случай похож на третий пример из предыдущей главы, в которой ошибка на тренировочной выборке так же равна 15% и ошибка на валидационной выборке 30%. Если оптимальная доля ошибки находится около 0%, тогда ошибка на тренировочной выборке в 15% дает большое пространство для работ по улучшению алгоритма. При таком предположении, усилия, направленные на уменьшение смещения в работе алгоритма могут быть весьма плодотворны. Но если оптимальная доля ошибок классификации не может быть ниже 14%, то аналогичная доля ошибок алгоритма на тренировочной выборке (т. е. в районе 14-15%) говорит о том, что возможности по уменьшению смещения практически исчерпаны.
Для задач, в которых оптимальная доля ошибок классификации существенно отличается от нуля, можно предложить более подробную структуризацию ошибок. Продолжим рассматривать приведенный выше пример с распознаванием речи, общая ошибка в 30% на валидационной выборке может быть разложена на следующие составные части (таким же образом можно анализировать ошибки на тестовой выборке):
- Оптимальное смещение (unavoidable bias): 14%. Представим, мы решили, что даже возможно наилучшая система распознавания речи в мире, будет иметь долю ошибки в 14%. Мы будем говорить об этом, как о «неустранимой» (unavoidable) части смещения обучающегося алгоритма.
- Устранимое смещение (Avoidable bias): 1%. Эта величина рассчитывается как разница между долей ошибок на тренировочной выборке и оптимальной долей ошибок.
замечание автора: Если данная величина получилась отрицательной, таким образом, ваш алгоритм на тренировочной выборке показывает меньшую ошибку, чем «оптимальная». Это означает, что вы переобучились на тренировочной выборке, ваш алгоритм запомнил примеры (и их классы) тренировочной выборки. В этом случае вы должны сосредоточиться на методах уменьшения разброса, а не на дальнейшем уменьшении смещения.
- Разброс (Variance): 15%. Разница между ошибками на тренировочной выборке и на валидационной выборке
Соотнеся это с нашими прежними определениями, смещение и устранимое смещение связаны следующим образом:
Смещение (bias) = Оптимальное смещение ( «unavoidable bias» ) + Устранимое смещение ( «avoidable bias» )
замечание автора: Эти определения выбраны для лучшего объяснения, как можно улучшить качество работы обучающегося алгоритма. Эти определения отличаются от формальных определений смещения и разброса, принятых в статистике. Технически то, что я определяю, как «Смещение» следовало бы назвать «ошибкой, которая заложена в структуре данных, (ее нельзя выявить и устранить)» и «Устранимое смещение» нужно определить, как «Смещение обучающегося алгоритма, которая превышает оптимальное смещение».
Устранимое смещение (avoidable bias) показывает, насколько хуже качество вашего алгоритма на тренировочной выборке, чем качество «оптимального классификатора».
Основная идея разброса (variance) остается прежней. В теории мы всегда можем уменьшить разброс практически до нуля, тренируясь на достаточно большой тренировочной выборке. Таким образом любой разброс является «устранимым» (avoidable) при наличие достаточно большой выборки, поэтому не может быть такого понятия, как «неустранимый разброс» (unavoidable variance).
Рассмотрим еще один пример, в котором оптимальная ошибка составляет 14% и мы имеем:
- Ошибка на тренировочной выборке = 15%
- Ошибка на валидационной выборке = 16%
В предыдущей главе классификатор с такими показателями мы оценивали, как классификатор с высоким смещением, в текущих условиях мы скажем, что «устранимое смещение» (avoidable bias) составляет 1%, и разброс составляет порядка 1%. Таким образом, алгоритм уже работает достаточно хорошо и почти нет резервов для улучшения качества его работы. Качество работы данного алгоритма всего на 2% ниже оптимального.
Из этих примеров понятно, что знание величины неустранимой ошибки полезно для принятия решения о дальнейших действиях. В статистике оптимальную долю ошибки называют так же ошибкой Байеса ( Bayes error rate ).
Как узнать размер оптимальной доли ошибки? Для задач, с которыми хорошо справляется человек, таких как распознавание изображений или расшифровка аудио клипов, можно попросить асессоров разметить данные, а потом измерить точность человеческой разметки на тренировочной выборке. Это даст оценку оптимальной доли ошибок. Если вы работаете над проблемой, с которой сложно справиться даже человеку (например, предсказать, какой фильм рекомендовать или какую рекламу показать пользователю), в этом случае довольно тяжело оценить оптимальную долю ошибок.
В разделе «Сравнение с человеческим уровнем качества» (Comparing to Human-Level Performance, главы с 33 по 35), я буду более подробно обсуждать процесс сравнения качества работы обучающегося алгоритма с уровнем качества, которого может достигнуть человек.
В последних главах, вы узнали, как оценивать устранимые / неустранимые смещение и разброс, анализируя долю ошибок классификатора на тренировочной и валидационной выборках. В следующей главе будет рассмотрено, как вы можете использовать выводы из такого анализа для принятия решения о том, сконцентрироваться на методах, уменьшающих смещение или на методах, которые уменьшают разброс. Подходы к борьбе со смещением сильно отличаются от подходов к уменьшению разброса, поэтому техники, которые вы должны применять в вашем проекте для улучшения качества, сильно зависят от того, что является проблемой на настоящий момент — большое смещение или большой разброс.
Читайте дальше!
23 Устранение смещения и разброса
Приведем простую формулу устранения смещения и разброса:
- Если у вас большое устранимое смещение (avoidable bias), увеличьте сложность вашей модели (например, увеличьте вашу нейронную сеть, добавив слоев или (и) нейронов)
- Если у вас большой разброс, добавьте примеров в вашу тренировочную выборку
Если у вас есть возможность увеличивать размер нейронной сети и безлимитно добавлять данные в тренировочную выборку, это поможет добиться хорошего результата для большого количества задач машинного обучения.
На практике увеличение размера модели в конечном счете вызовет вычислительные сложности, так как обучение очень больших моделей происходит медленно. Также вы можете исчерпать лимит доступных для обучения данных. (Даже во всем Интернете количество изображений с кошками конечно!)
Различные архитектуры моделей алгоритмов, например, различные архитектуры нейронных сетей, будут давать различные значения для смещения и разброса, применительно к вашей задаче. Вал недавних исследований в области глубинного обучения позволил создать большое количество инновационных архитектур моделей нейронных сетей. Таким образом, если вы используете нейронные сети, научная литература может быть прекрасным источником для вдохновения. Также имеется большое количество отличных реализаций алгоритмов в открытых источниках, например на GitHub. Однако, результаты попыток использовать новые архитектуры существенно менее предсказуемые, чем приведенная выше простая формула — увеличивайте размер модели и добавляйте данные.
Увеличение размера модели обычно уменьшает смещение, но оно же может вызвать увеличение разброса, также возрастает риск переобучения. Однако, проблема переобучения встает только тогда, когда вы не используете регуляризацию. Если включить хорошо спроектированный метод регуляризации в модель, обычно удается безопасно увеличить размер модели, не допустив переобучения.
Предположим, вы применяете глубокое обучение, используя L2 регуляризацию или dropout (Замечание переводчика: про Dropout можно почитать, например, здесь: https://habr.com/company/wunderfund/blog/330814/), используя параметры регуляризации, безупречно работающие на валидационной выборке. Если вы увеличите размер модели, обычно качество работы вашего алгоритма остается таким же или вырастает; его существенное снижение маловероятно. Единственная причина, из-за которой приходится отказываться от увеличения размера модели — большие вычислительные издержки.
24 Компромисс между смещением и разбросом
Вы могли слышать о «компромиссе между смещением и разбросом». Среди множества изменений, которые можно внести в обучающиеся алгоритмы, встречаются такие, которые уменьшают смещение и увеличивают разброс или наоборот. В таком случае говорят о «компромиссе» между смещением и разбросом.
Например, увеличение размерам модели — добавление нейронов и (или) слоев нейронной сети, или добавление входных признаков обычно уменьшают смещение, но могут увеличить разброс. Наоборот, добавление регуляризации часто увеличивает смещение, но уменьшает разброс.
На сегодняшний день у нас обычно есть доступ к большому количеству данных и вычислительных мощностей хватает для обучения больших нейронных сетей (для глубокого обучения). Таким образом, проблема компромисса не стоит так остро, и в нашем распоряжении есть много инструментов для уменьшения смещения, не навредив сильно значению разброса и наоборот.
Например, обычно вы можете увеличить размер нейронной сети и настроить регуляриацию таким образом, чтобы уменьшить смещение без заметного увеличения разброса. Добавление данных в тренировочную выборку, так же, как правило, уменьшает разброс, не влияя на смещение.
Если удачно подобрать архитектуру модели, хорошо соответствующую задаче, можно одновременно уменьшить и смещение и разброс. Но выбор такой архитектуры может оказаться сложной задачей.
В следующих нескольких главах, мы обсудим другие специфические техники, направленные на борьбу со смещением и разбросом.
25 Подходы к уменьшению устранимого смещения
Если ваш обучающийся алгоритм страдает большим устранимым смещением, вы можете попробовать следующие подходы:
- Увеличение размеров модели (такие, как количество нейронов и слоев): этот подход уменьшает смещение, таким образом у вас появляется возможность лучше подгонять алгоритм к тренировочной выборке. Если вы обнаружили, что при этом увеличивается разброс, используйте регуляризацию, которая обычно устраняет увеличение разброса.
- Модифицируйте входящие признаки, основываясь на идеях, пришедших при анализе ошибок. Предположим анализ ошибок побудил вас создать новые дополнительные признаки, которые помогают алгоритму избавиться от определенной категории ошибок (в следующих главах мы обсудим этот аспект). Эти новые признаки могут помочь как со смещением, так и с разбросом. В теории добавление новых признаков может увеличить разброс; но если такое случится, вы всегда можете использовать регуляризацию, которая, как правило, помогает справиться с увеличением разброса.
- Уменьшение или отказ от регуляризации (L2 регуляризация, L1 регуляризация, Dropout): этот подход уменьшает устранимое смещение, однако, приводит к росту разброса.
- Модификация архитектуры модели (например, архитектуры нейронной сети) чтобы она больше подходила для вашей задачи: Этот подход влияет как на разброс, так и на смещение
Один не очень полезный метод:
- Добавление данных в тренировочную выборку: Этот подход помогает уменьшать разброс, но обычно не оказывает существенного воздействия на смещение.
26 Анализ ошибок на тренировочной выборке
Только после хорошего качества алгоритма на тренировочной выборке, можно ожидать от него приемлемых результатов на валидационной/тестовой выборках.
В дополнение к методам, описанным ранее, применяемым к большому смещению, я иногда так же переношу анализ ошибок на данные тренировочной выборки, следуя тому же подходу, который использовался при анализе валидационной выборки глазного яблока. Это может помочь, если ваш алгоритм имеет высокое смещение, т. е. если алгоритм не смог хорошо обучиться на тренировочной выборке.
Например, предположим вы разрабатываете систему распознавания речи для какого-то приложения и собрали тренировочную выборку аудио клипов от волонтеров. Если ваша система не работает хорошо на тренировочной выборке, вы можете рассмотреть возможность прослушивания набора, состоящего из 100 примеров, на которых алгоритм отработал плохо для того, чтобы понять основные категории ошибок на тренировочной выборке. Аналогично анализу ошибок на валидационной выборке, вы можеет посчитать ошибки в разрезе категорий:
В этом примере вы могли бы понять, что ваш алгоритм испытывает особенные трудности с тренировочными примерами, имеющих много фонового шума. Таким образом вы можете сфокусироваться на методах, которые позволят ему лучше работать на тренировочных примерах с фоновым шумом.
Вы так же можете повторно проверить, насколько человек может разобрать такие аудио-клипы, дав ему послушать те же записи, что и обучающемуся алгоритму. Если в них настолько много фонового шума, что просто невозможно кому-либо понять, что там говорят, тогда может быть бессмысленно ожидать, что какой-либо алгоритм правильно распознает такое произношение. Мы обсудим в дальнейших главах пользу, которую приносит сравнение качества работы нашего алгоритма с уровнем качества, доступным человеку.
27 Подходы к уменьшению разброса
Если ваш алгоритм страдает от большого разброса, вы можете попробовать следующие подходы:
- Добавить больше данных в тренировочную выборку: Это наиболее простой и реализуемый путь к уменьшению разброса, он работает до тех пор, пока у вас есть возможность существенно увеличивать количество используемых данных и имеется достаточно вычислительных мощностей для их обработки.
- Добавить регуляризацию (L1 регуляризация, L2 регуляризация, dropout): этот подход уменьшает разброс, но увеличивает смещение.
- Добавить раннюю остановку (т. е. остановить градиентный спуск раньше, базируясь на значении ошибки на валидационной выборке): Эта техника уменьшает разброс, но увеличивает смещение. Ранняя остановка сильно напоминает метод регуляризации, поэтому некоторые авторы относят ее к регуляризации.
- Отбор признаков для уменьшения количества/типов входящих признаков: Этот подход может помочь с проблемой разброса, но также может увеличить смещение. Незначительное уменьшение количества признаков (скажем, с 1000 признаков до 900) вряд ли окажет большой эффект на смещение. Существенное уменьшение (скажем от 1000 признаков до 100 или 10 кратное уменьшение) более вероятно окажет существенный эффект, эффект будет увеличиваться до тех пор, пока вы не исключите слишком много полезных признаков. В современном глубинном обучении, когда данных много, происходит отход от тщательного отбора признаков, и сегодня мы скорее всего возьмем все признаки, которые у нас есть и будем на них обучать алгоритм, давая возможность алгоритму самому решить, какие из них использовать, базируясь на большом количестве обучающих примеров. Однако, если ваша тренировочная выборка маленькая, отбор признаков может оказаться очень полезным.
- Уменьшение размера (сложности) модели (такие как количество нейронов / слоев). Используйте с осторожностью! Этот подход может уменьшить разброс и одновременно, возможно, увеличит смещение. Однако, я бы не стал рекомендовать этот подход для уменьшения разброса. Добавление регуляризации обычно приводит к лучшему качеству классификации. Преимуществом уменьшения размера модели является уменьшение вашей потребности в вычислительных мощностях и таким образом ускоряется процесс тренировки моделей. Если увеличение скорости тренировки моделей будет полезным, тогда нужно рассмотреть вариант с уменьшением размера модели. Однако, если вашей задачей является только уменьшение разброса и вы не испытываете дефицита вычислительных мощностей, лучше рассмотреть возможности дополнительной регуляризации.
Здесь я привожу два дополнительных тактических приема, повторяя сказанное в предыдущих главах, применительно к уменьшению смещения:
- Модифицируйте входящие признаки, базируясь на понимании, полученном из анализа ошибок: Скажем, ваша анализ ошибок привел к идеи о том, что можно создать дополнительные признаки, которые помогут алгоритму избавиться от некоторых категорий ошибок. Эти новые признаки помогут уменьшить и разброс и смещение. Теоретически, добавление новых признаков может увеличить разброс; но если это случится, вы всегда можете воспользоваться регуляризацией, которая обычно нивелирует увеличение разброса.
- Модифицируйте архитектуру модели (например, архитектуру нейронной сети) делая ее более подходящей для вашей задачи: Этот подход может уменьшить и смещение и разброс.
продолжение
11.2. Оценка результатов выборочного наблюдения
11.2.1. Средняя и предельная ошибки выборки. Построение доверительных границ для средней и доли
Средняя ошибка выборки показывает, насколько отклоняется в среднем параметр выборочной совокупности от соответствующего параметра генеральной. Если рассчитать среднюю из ошибок всех возможных выборок определенного вида заданного объема (n), извлеченных из одной и той же генеральной совокупности, то получим их обобщающую характеристику — среднюю ошибку выборки (
В теории выборочного наблюдения выведены формулы для определения 
Например, если применяется повторная собственно случайная выборка, то 


При бесповторном собственно случайном отборе в формулы вносится поправка (1 — n/N):


Вероятность получения именно такой величины ошибки всегда равна 0,683. На практике же предпочитают получать данные с большей вероятностью, но это приводит к возрастанию величины ошибки выборки.
Предельная ошибка выборки (

Если ошибку выборки увеличить в два раза (t = 2), то получим гораздо большую вероятность того, что она не превысит определенного предела (в нашем случае — двойной средней ошибки) — 0,954. Если взять t = 3, то доверительная вероятность составит 0,997 — практически достоверность.
Уровень предельной ошибки выборки зависит от следующих факторов:
- степени вариации единиц генеральной совокупности;
- объема выборки;
- выбранных схем отбора (бесповторный отбор дает меньшую величину ошибки);
- уровня доверительной вероятности.
Если объем выборки больше 30, то значение t определяется по таблице нормального распределения, если меньше — по таблице распределения Стьюдента.
Приведем некоторые значения коэффициента доверия из таблицы нормального распределения.
| Значение доверительной вероятности P | 0,683 | 0,954 | 0,997 |
|---|---|---|---|
| Значение коэффициента доверия t | 1,0 | 2,0 | 3,0 |
Доверительный интервал для среднего значения признака и для доли в генеральной совокупности устанавливается следующим образом:
Итак, определение границ генеральной средней и доли состоит из следующих этапов:
Ошибки выборки при различных видах отбора
- Собственно случайная и механическая выборка. Средняя ошибка собственно случайной и механической выборки находятся по формулам, представленным в табл. 11.3.
 |
|
где |
Пример 11.2. Для изучения уровня фондоотдачи было проведено выборочное обследование 90 предприятий из 225 методом случайной повторной выборки, в результате которого получены данные, представленные в таблице.
| Уровень фондоотдачи, руб. | До 1,4 | 1,4-1,6 | 1,6-1,8 | 1,8-2,0 | 2,0-2,2 | 2,2 и выше | Итого |
|---|---|---|---|---|---|---|---|
| Количество предприятий | 13 | 15 | 17 | 15 | 16 | 14 | 90 |
В рассматриваемом примере имеем 40%-ную выборку (90 : 225 = 0,4, или 40%). Определим ее предельную ошибку и границы для среднего значения признака в генеральной совокупности по шагам алгоритма:
- По результатам выборочного обследования рассчитаем среднее значение и дисперсию в выборочной совокупности:
| Результаты наблюдения | Расчетные значения | |||
|---|---|---|---|---|
| уровень фондоотдачи, руб., xi | количество предприятий, fi | середина интервала, xixb4 | xixb4fi | xixb42fi |
| До 1,4 | 13 | 1,3 | 16,9 | 21,97 |
| 1,4-1,6 | 15 | 1,5 | 22,5 | 33,75 |
| 1,6-1,8 | 17 | 1,7 | 28,9 | 49,13 |
| 1,8-2,0 | 15 | 1,9 | 28,5 | 54,15 |
| 2,0-2,2 | 16 | 2,1 | 33,6 | 70,56 |
| 2,2 и выше | 14 | 2,3 | 32,2 | 74,06 |
| Итого | 90 | — | 162,6 | 303,62 |
Выборочная средняя
Выборочная дисперсия изучаемого признака
- Определяем среднюю ошибку повторной случайной выборки
- Зададим вероятность, на уровне которой будем говорить о величине предельной ошибки выборки. Чаще всего она принимается равной 0,999; 0,997; 0,954.
Для наших данных определим предельную ошибку выборки, например, с вероятностью 0,954. По таблице значений вероятности функции нормального распределения (см. выдержку из нее, приведенную в Приложении 1) находим величину коэффициента доверия t, соответствующего вероятности 0,954. При вероятности 0,954 коэффициент t равен 2.
- Предельная ошибка выборки с вероятностью 0,954 равна
- Найдем доверительные границы для среднего значения уровня фондоотдачи в генеральной совокупности
Таким образом, в 954 случаях из 1000 среднее значение фондоотдачи будет не выше 1,88 руб. и не ниже 1,74 руб.
Выше была использована повторная схема случайного отбора. Посмотрим, изменятся ли результаты обследования, если предположить, что отбор осуществлялся по схеме бесповторного отбора. В этом случае расчет средней ошибки проводится по формуле
Тогда при вероятности равной 0,954 величина предельной ошибки выборки составит:
Доверительные границы для среднего значения признака при бесповторном случайном отборе будут иметь следующие значения:
Сравнив результаты двух схем отбора, можно сделать вывод о том, что применение бесповторной случайной выборки дает более точные результаты по сравнению с применением повторного отбора при одной и той же доверительной вероятности. При этом, чем больше объем выборки, тем существеннее сужаются границы значений средней при переходе от одной схемы отбора к другой.
По данным примера определим, в каких границах находится доля предприятий с уровнем фондоотдачи, не превышающим значения 2,0 руб., в генеральной совокупности:
- рассчитаем выборочную долю.
Количество предприятий в выборке с уровнем фондоотдачи, не превышающим значения 2,0 руб., составляет 60 единиц. Тогда
m = 60, n = 90, w = m/n = 60 : 90 = 0,667;
- рассчитаем дисперсию доли в выборочной совокупности

- средняя ошибка выборки при использовании повторной схемы отбора составит
Если предположить, что была использована бесповторная схема отбора, то средняя ошибка выборки с учетом поправки на конечность совокупности составит
- зададим доверительную вероятность и определим предельную ошибку выборки.
При значении вероятности Р = 0,997 по таблице нормального распределения получаем значение для коэффициента доверия t = 3 (см. выдержку из нее, приведенную в Приложении 1):
- установим границы для генеральной доли с вероятностью 0,997:
Таким образом, с вероятностью 0,997 можно утверждать, что в генеральной совокупности доля предприятий с уровнем фондоотдачи, не превышающим значения 2,0 руб., не меньше, чем 54,7%, и не больше 78,7%.
- Типическая выборка. При типической выборке генеральная совокупность объектов разбита на k групп, тогда
N1 + N2 + … + Ni + … + Nk = N.
Объем извлекаемых из каждой типической группы единиц зависит от принятого способа отбора; их общее количество образует необходимый объем выборки
n1 + n2 + … + ni + … + nk = n.
Существуют следующие два способа организации отбора внутри типической группы: пропорциональной объему типических групп и пропорциональной степени колеблемости значений признака у единиц наблюдения в группах. Рассмотрим первый из них, как наиболее часто используемый.
Отбор, пропорциональный объему типических групп, предполагает, что в каждой из них будет отобрано следующее число единиц совокупности:
n = ni · Ni/N
где ni — количество извлекаемых единиц для выборки из i-й типической группы;
n — общий объем выборки;
Ni — количество единиц генеральной совокупности, составивших i-ю типическую группу;
N — общее количество единиц генеральной совокупности.
Отбор единиц внутри групп происходит в виде случайной или механической выборки.
Формулы для оценивания средней ошибки выборки для среднего и доли представлены в табл. 11.6.

|
Здесь 
Пример 11.3. В одном из московских вузов проведено выборочное обследование студентов с целью определения показателя средней посещаемости вузовской библиотеки одним студентом за семестр. Для этого была использована 5%-ная бесповторная типическая выборка, типические группы которой соответствуют номеру курса. При отборе, пропорциональном объему типических групп, получены следующие данные:
| Номер курса | Всего студентов, чел., Ni | Обследовано в результате выборочного наблюдения, чел., ni | Среднее число посещений библиотеки одним студентом за семестр, xi | Внутригрупповая выборочная дисперсия, 
|
|---|---|---|---|---|
| 1 | 650 | 33 | 11 | 6 |
| 2 | 610 | 31 | 8 | 15 |
| 3 | 580 | 29 | 5 | 18 |
| 4 | 360 | 18 | 6 | 24 |
| 5 | 350 | 17 | 10 | 12 |
| Итого | 2 550 | 128 | 8 | — |
Число студентов, которое необходимо обследовать на каждом курсе, рассчитаем следующим образом:
- общий объем выборочной совокупности:
n = 2550/130*5 =128 (чел.);
- количество единиц, отобранных из каждой типической группы:
аналогично для других групп:
n2 = 31 (чел.);
n3 = 29 (чел.);
n4 = 18 (чел.);
n5 = 17 (чел.).
Проведем необходимые расчеты.
- Выборочная средняя, исходя из значений средних типических групп, составит:
- Средняя из внутригрупповых дисперсий
- Средняя ошибка выборки:
С вероятностью 0,954 находим предельную ошибку выборки:
- Доверительные границы для среднего значения признака в генеральной совокупности:
Таким образом, с вероятностью 0,954 можно утверждать, что один студент за семестр посещает вузовскую библиотеку в среднем от семи до девяти раз.
- Малая выборка. В связи с небольшим объемом выборочной совокупности те формулы для определения ошибок выборки, которые использовались нами ранее при «больших» выборках, становятся неподходящими и требуют корректировки.
Среднюю ошибку малой выборки определяют по формуле
Предельная ошибка малой выборки:
Распределение значений выборочных средних всегда имеет нормальный закон распределения (или приближается к нему) при п > 100, независимо от характера распределения генеральной совокупности. Однако в случае малых выборок действует иной закон распределения — распределение Стьюдента. В этом случае коэффициент доверия находится по таблице t-распределения Стьюдента в зависимости от величины доверительной вероятности Р и объема выборки п. В Приложении 1 приводится фрагмент таблицы t-распределения Стьюдента, представленной в виде зависимости доверительной вероятности от объема выборки и коэффициента доверия t.
Пример 11.4. Предположим, что выборочное обследование восьми студентов академии показало, что на подготовку к контрольной работе по статистике они затратили следующее количество часов: 8,5; 8,0; 7,8; 9,0; 7,2; 6,2; 8,4; 6,6.
Оценим выборочные средние затраты времени и построим доверительный интервал для среднего значения признака в генеральной совокупности, приняв доверительную вероятность равной 0,95.
- Среднее значение признака в выборке равно
- Значение среднего квадратического отклонения составляет
- Средняя ошибка выборки:
- Значение коэффициента доверия t = 2,365 для п = 8 и Р = 0,95 .
- Предельная ошибка выборки:
- Доверительный интервал для среднего значения признака в генеральной совокупности:
То есть с вероятностью 0,95 можно утверждать, что затраты времени студента на подготовку к контрольной работе находятся в пределах от 6,9 до 8,5 ч.
11.2.2. Определение численности выборочной совокупности
Перед непосредственным проведением выборочного наблюдения всегда решается вопрос, сколько единиц исследуемой совокупности необходимо отобрать для обследования. Формулы для определения численности выборки выводят из формул предельных ошибок выборки в соответствии со следующими исходными положениями (табл. 11.7):
- вид предполагаемой выборки;
- способ отбора (повторный или бесповторный);
- выбор оцениваемого параметра (среднего значения признака или доли).
Кроме того, следует заранее определиться со значением доверительной вероятности, устраивающей потребителя информации, и с размером допустимой предельной ошибки выборки.
 |
Примечание: при использовании приведенных в таблице формул рекомендуется получаемую численность выборки округлять в большую сторону для обеспечения некоторого запаса в точности.
Пример 11.5. Рассчитаем, сколько из 507 промышленных предприятий следует проверить налоговой инспекции, чтобы с вероятностью 0,997 определить долю предприятий с нарушениями в уплате налогов. По данным прошлого аналогичного обследования величина среднего квадратического отклонения составила 0,15; размер ошибки выборки предполагается получить не выше, чем 0,05.
При использовании повторного случайного отбора следует проверить
При бесповторном случайном отборе потребуется проверить
Как видим, использование бесповторного отбора позволяет проводить обследование гораздо меньшего числа объектов.
Пример 11.6. Планируется провести обследование заработной платы на предприятиях отрасли методом случайного бесповторного отбора. Какова должна быть численность выборочной совокупности, если на момент обследования в отрасли число занятых составляло 100 000 чел.? Предельная ошибка выборки не должна превышать 100 руб. с вероятностью 0,954. По результатам предыдущих обследований заработной платы в отрасли известно, что среднее квадратическое отклонение составляет 500 руб.
Следовательно, для решения поставленной задачи необходимо включить в выборку не менее 100 человек.

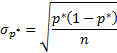
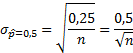
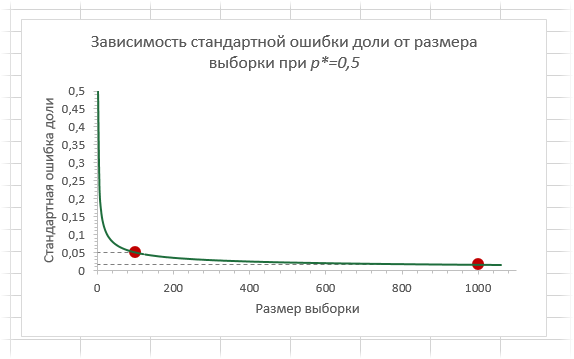






















 ) при использовании типического отбора, пропорционального объему типических групп
) при использовании типического отбора, пропорционального объему типических групп














