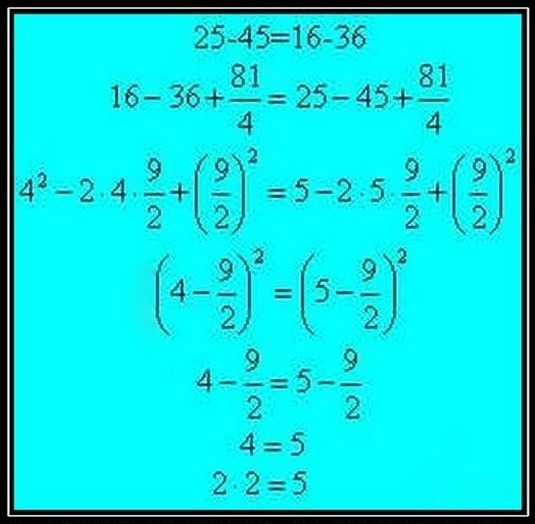-
-
February 9 2017, 08:56
- Философия
- Cancel
Использован фрагмент 
Знаете, что такое софизмы?
Согласно Большому энциклопедическому словарю софизм это мнимое доказательство, в котором обоснованность заключения кажущаяся, порождается чисто субъективным впечатлением, вызванным недостаточностью логического или семантического анализа.
Вот типичный пример математического софизма, в котором доказано, что «2*2=5″…
[Нажмите, чтобы прочитать доказательство]
Вы с этим согласны?
Логика подсказывает, что где то кроется ошибка.
Что поможет её найти? Знание основ математики.
[Нажмите, чтобы прочитать ответ]Ошибка кроется в 5 строке «доказательства» — неправильно опущены скобки.
Вариант попроще[Spoiler (click to open)]
И вообще:
Весёлая задача. Но разумеется она не доказывает что дважды два равно пять. Автор воспользовался известной формулой (A + B)^2 = A^2 + 2AB + B^2 Применил её для получения левой части из правой. И не смотря на опечаточку, забыл над цифрой пять поставить квадратик, получил правильный результат
(4 — 9/2)^2 = (5 — 9/2)^2.
Однако всем кто знаком с арифметикой известно что для любого положительного числа существуют два числа возведение в квадрат которых даёт данное число, квадрат иногда и меня приводил к подобной ошибке (Хотя возможно автор нашёл, а может и сам придумал эту задачку просто что-бы кто-то лишний раз немного подумал)
Например:
a^2 = 4 => a = -2 или a = +2
То есть когда мы берём корень избавляясь от чётной степени то получаем два возможных случая.
Например
(x + 5)^2 = 16 => x + 5 = 4 или x + 5 = -4
Так и в данном случае:
(4 — 9/2)^2 = (5 — 9/2)^2 => 4 — 9/2 = +(5 — 9/2) или 4 — 9/2 = -(5 — 9/2)
В первом случае: 4 — 9/2 = +(5 — 9/2) => 4=5 (Не верно)
Во втором случае: 4 — 9/2 = -(5 — 9/2) => 4 — 4 — 1/2 = -5 + 4 + 1/2 =>
4 — 4 = -5 + 4 +1 => 0=0 (Верно!!!)
Вот и вся история.
Важно так-же запомнить, (Сколько раз я наступал на эти грабли учась в школе)
Уравнение f^2(x) = g^2(x) приводит к двум уравнениям, если имеет смысл избавиться от квадратов: f(x) = +g(x) и f(x) = -g(x). Решения этих двух уравнений являются и решениями исходного уравнения f^2(x) = g^2(x).
И наоборот решения уравнения f^2(x) = g^2(x) являются решениями и не менее одного уравнения полученного после избавления от квадратов
Если имеет смысл возвести в квадрат уравнение f(x) = g(x) и дальше решать уравнение
f^2(x) = g^2(x). То решениями уравнеия f^2(x) = g^2(x) будут и решения уравнения
f(x) = -g(x). И могут появиться лишние корни.
Вот наверное и всё что можно сказать по данному вопросу. Ну и поблагодарить автора за интересную задачку.
Действительно есть случаи, когда дважды два равно пяти. Я могу привести два варианта, как и почему такое может быть. Один вариант тут уже указан: это вычисление с применением обычных математических приемов. Тут нет ничего сложного, и даже если вы учились давно, то вам не составит труда проследить вычисления и признать, что действительно этот пример показывает, что два на два — это пять. Я приведу то же вычисление, которое указано в вопросе, только в более удобном виде, с правильными скобками. Итак, как решить задачу, что дважды два равно пяти:
Поначалу я тоже усомнился, но потом дважды всё пересчитал и понял, что эти действия верны, и действительно в какой-то момент мы получаем, что 2х2 = 5. Те, кто очень хорошо помнит школьный курс математики, поймет, в чем тут соль:
Минусовое число нельзя вынести из-под скобок во второй степени. Такая ситуация, как здесь, считается не имеющей решения. То есть математики даже не пытаются объяснить, как так получается, они просто говорят: ну, раз это противоречит понятным нам правилам, то давайте просто это запретим!
Казалось бы, это — что-то вроде шутки, маленький пример. Но такой пример 2х2 = 5 показывает несостоятельность школьной системы образования: мало кто из учителей сможет достойно объяснить ученикам, почему такая ситуация невозможна, и сохранить свой авторитет. Именно об этом говорят многие заслуженные педагоги: проблема не в информации, не в задаче, а в том, способен ли преподаватель объяснить ученикам эту задачу.
Но если отвлечься от математики, то сама жизнь показывает нам, что дважды два равно пяти. Например, если четыре человека объединят свои усилия, будут работать в слаженной команде, то результат будет такой, словно работали не четверо, а все пять. Так математика легко перетекает в философию.
Описание презентации по отдельным слайдам:
-
1 слайд
Докажем, что
2 x 2 = 5 -
2 слайд
Доказательство :
Имеем верное числовое равенство
4:4=5:5.
Вынесем за скобки в каждой части его общий множитель. Получим:
4(1:1)=5(1:1).
Числа в скобках равны, поэтому
4=5,или
2 x 2 = 5. -
3 слайд
Найдите ошибку в следующих рассуждениях
Имеем верное числовое равенство
4:4=5:5.
Вынесем за скобки в каждой части его общий множитель. Получим:
4(1:1)=5(1:1).
Числа в скобках равны, поэтому
4=5,или
2 x 2 = 5. -
4 слайд
Найдите ошибку в следующих рассуждениях
Имеем верное числовое равенство
4:4=5:5.
Вынесем за скобки в каждой части его общий множитель. Получим:
4(1:1)=5(1:1).
Числа в скобках равны, поэтому
4=5,или
2 x 2 = 5. -
5 слайд
Ай, ай, ай…
Разве можно использовать распределительное свойство для деления?!
В этом софизме ошибка в вынесении за скобки общего множителя. 4(1:1)=5(1:1).
Распределительное свойство нельзя применять при делении!!! -
6 слайд
Еще одно доказатьльство
Нам как-то учительница математики сказала что 2*2=5 и обещала обяснить это на
факультативе. Мне на него не удалось попасть (из лени:)), да вскоре я забыл об этом.
Вспомнил вчера и залез в интернет.
Любителям математики посвещаеться.
2*2=5
Доказательство:
то есть 4=5
25 — 45 = 16 — 36
Далее прибавим (9/2)^2 ко обеим частям ур-ия:
25 — 45 + (9/2)^2 = 16 — 36 + (9/2)^2
5^2 — (2*5*9)/2 + (9/2)^2 = 4^2 — (2*4*9)/2 + (9/2)^2
(5-9/2)^2 = (4-9/2)^2, обе части положительны, можно извлечь квадратный корень
5 — 9/2 = 4 — 9/2
Далее прибавим 9/2 ко обеим частям ур-ия:
5 = 4 что и требовалось доказать
Следовательно 2*2 = 5
2+2=5
Доказательство:
Пyсть 2+2=5.
2*1 + 2*1 = 5*1
Распишем 1, как частное pавных чисел:
1 = (5-5)/(5-5)
Тогда:
2*(5-5)/(5-5) + 2*(5-5)/(5-5) = 5*(5-5)/(5-5)
Умножим левyю и пpавyю части на (5-5), тогда:
2*(5-5) + 2*(5-5) = 5*(5-5)
Отсюда:
0 + 0 = 0
Портал Проза.ру предоставляет авторам возможность свободной публикации своих литературных произведений в сети Интернет на основании пользовательского договора. Все авторские права на произведения принадлежат авторам и охраняются законом. Перепечатка произведений возможна только с согласия его автора, к которому вы можете обратиться на его авторской странице. Ответственность за тексты произведений авторы несут самостоятельно на основании правил публикации и законодательства Российской Федерации. Данные пользователей обрабатываются на основании Политики обработки персональных данных. Вы также можете посмотреть более подробную информацию о портале и связаться с администрацией.
Ежедневная аудитория портала Проза.ру – порядка 100 тысяч посетителей, которые в общей сумме просматривают более полумиллиона страниц по данным счетчика посещаемости, который расположен справа от этого текста. В каждой графе указано по две цифры: количество просмотров и количество посетителей.
© Все права принадлежат авторам, 2000-2022. Портал работает под эгидой Российского союза писателей. 18+
2+2=5 В чем тут подвох?
Во первых, 5-5=0, а всем известно, что на ноль делить нельзя.
А во-вторых, (5-5)/(5-5)=0/0. И разве это равно единице?)) Конечно же ни коем образом!
Это просто для отвода глаз написали, чтобы невнимательные люди не заметили подвоха.
Даже не вдумываясь в приведенное решение, достаточно просто обратить внимание на один и примеров в данном доказательстве, а именно на пример — 1 = (5-5)/(5-5).
Если участь что действия в скобках будут равны нулю, то подвох кроется в том, что на 0 делить нельзя.
Доказательств данного тождества существует множество, ниже я приведу одно из них. Но то, которое написал автор вопроса является ошибочным, поскольку одно из действий подразумевает деление на ноль, что в математике считается бессмысленным, поскольку результат не может быть определен.
Итак, попробуйте опровергнуть такой вариант:
Начнем с того, что:
То же самое: 16-36 = 25-45
Можно выразить следующим образом:
1 = (5-5)/(5-5) — это бред. Деление на ноль. Получается 1=0/0. Такого быть не может
Здравствуйте 2+2=4 и 2*2=4
Мне очень интересно вы посчитайте тогда пальцы 1. 2. 3. 4. 5. 6. 7. 8. 9. 10
10 пальцев на руках а если сложить 2 пальца и 2 пальца = 4 пальца а по вашей логике у меня должен вырасти 5тый палец вы что смеётесь ?
Вы не будьте дебилами науке американцы тупые они доказывали что пчела не может летать из за своего веса а муравей не может поднять больше своего веса в 10 раз так как его тела мало весит он не сможет понять что бы либо больше в 10 раз но он поднимает но есть загвоздка попробуйте поднять больше своего веса хотя бы в 5 раз вашего веса не хватит с физичикой теории так как вам придётся вытянуть руки в низ и поднимать в верх Но можно хитрый способ с физичиского бока так говоря взять рычаг и подтянуть в верх над телом и отпустить на руки вытянутые в верх под опорой ваших костей кто-торые могут выдержать вес машины при условии что предмет вы возьмете не с низу
а с верху при правельной стойке вы выдержите в 5 раз больше своего веса но значит 2+2=5 может и такое быть в жизни всё бывает !
Мы докажем, что 2+2=5, и 95% из вас даже не поймут, в чем подвох
Над этой математической головоломкой бьются лучшие умы мира. А сегодня и вы можете попробовать решить эту задачку. Если вас не пугают неожиданные логические цепочки, обязательно попробуйте решить этот пример!
Знаете ли вы, что 2+2 может быть равно 5? Не торопитесь возмущаться, даже если в школе у вас было «отлично» по математике! Мы не разрушаем основные арифметические постулаты, а лишь предлагаем с неожиданной точки зрения рассмотреть этот простейший пример.
Итак, каким образом при сложении двоек может получиться пятерка? За основу возьмем 0, который также равен 0:
А если из 20 вычесть 20, а из 25 – 25, то мы вновь получим два нуля. Таким образом, получим математически и логически правильное равенство:
20 — 20 = 25 — 25
Следом представим число 20 как 4×5, а 25 – как 5×5. Поэтому далее получаем такое равенство:
(4 x 5) — (4 x 5) = (5 x 5) — (5 x 5)
А на следующем математическом действии с одинаковыми множителями просто выносим 4 в первой половине и 5 во второй части равенства за скобки. Получаем:
4 x (5 — 5) = 5 x (5 — 5)
Поскольку и в правой, и в левой части равенства одинаковые множители (5 — 5), то по правилам математики мы можем их не учитывать, то есть просто сократить. И получим следующее:
И наконец-то долгожданный финал, если 4 представить как (2 + 2):
2 + 2 = 5
А удалось ли вам осмыслить этот математический алгоритм? Где же тут подвох? Делитесь в комментариях и отправьте ссылку своим друзьям, чтобы взорвать и их чувствительный мозг!