Логические ошибки, встречающиеся в силлогизмах
§ 52. Некоторые из логических ошибок неправильного вывода, особенно часто встречающиеся в практике мышления, заслуживают быть особо отмеченными.
Одни из наиболее
частых здесь ошибок состоит в том, что,
умозаключая по первой фигуре, делают
вывод при отрицательной меньшей посылке.
Пример:
Все студенты
обязаны держать экзамены.
Аспиранты – не
студенты.
Аспиранты не
обязаны держать экзамены.
Вывод
явно ошибочный. Отрицательным вывод
может быть лишь при условии, если больший
термин будет распределён в большей
посылке. Но в большей посылке он, как
сказуемое утвердительного суждения,
выражающего подчинение понятия S
понятию Р, не распределен. Поэтому вывод
здесь логически невозможен.
Но
если он логически невозможен, то почему
же подобная ошибка возможна фактически?
– Одним из её источников является
неправильное истолкование смысла
большей посылки. Если, услышав, что «все
студенты обязаны держать экзамены», мы
истолкуем это положение в том смысле,
будто «одни лишь студенты обязаны
держать экзамены», то наш вывод примет
следующий вид:
Только
студенты обязаны держать экзамены.
Аспиранты – не
студенты.
Аспиранты не
обязаны держать экзамены.
Признав эти посылки
истинными, мы сделали из них правильный
вывод, т. е. вывод здесь необходимо
следует из принятых посылок. Ошибка
здесь не в том, что мы игнорировали
известное правило о распределённости
большего термина, распределённого в
выводе, а в том, что, неправильно истолковав
смысл большей посылки, мы получили
посылку, ложную по существу, а потому
получили и ложный вывод.
§ 53. Вторая встречающаяся в практике силлогистических выводов ошибка состоит в том, что делают вывод по второй фигуре из двух утвердительных посылок.
Пример:
Все рыбы имеют
плавники.
Это животное
имеет плавники.
Это животное –
рыба.
Здесь вывод – явно
ошибочный. Так как средний термин в
обеих посылках является предикатом
утвердительного суждения, выражающего
подчинение понятий, то он не распределён
ни в одной из посылок. Поэтому никакой
вывод здесь невозможен. И «рыбы» и «это
животное» входят в объём понятия
«животные, имеющие плавники». Но так
как из посылок неизвестно, в какую именно
часть этого объёма входят «рыбы» и в
какую –«это животное», то отношение
«этого животного» к «рыбам» остаётся
совершенно невыясненным; возможно, что
«это животное» и есть «рыба», и возможно,
что оно не есть «рыба».
Однако и в подобном
случае ошибка обычно состоит не столько
в нарушении известного правила о
распределённости среднего термина,
сколько в неправильном истолковании
смысла большей посылки. Кто, услышав
суждение «все рыбы имеют плавники»,
поймёт его в смысле «только рыбы имеют
плавники», тот, очевидно, сделает
следующий вывод:
Все животные,
имеющие плавники, – рыбы.
Это животное
имеет плавники.
Это животное есть
рыба.
В этом выводе
заключение было бы необходимо истинным,
если бы были истинными обе посылки. Но
большая посылка ложна, и потому вывод
также ложен.
§
54. Третья
ошибка, часто встречающаяся в практике
выводов, называется «учетверением
терминов» (qualernio
termi-norum).
Она состоит в том, что делают вывод из
двух посылок, в которые -входят не три,
а четыре термина.
Пример такой
ошибки:
Всякое сгорание
даёт в остатке золу и пепел.
Всякое окисление
есть сгорание.
Всякое окисление
даёт в остатке золу и пепел.
Так
как связь понятий, входящих в вывод, не
видна сразу, то она может быть установлена
только через третье понятие, отношение
которого к большему и меньшему терминам
было бы известно из посылок. Но в нашем
примере эта связь не может быть
установлена: здесь в посылках
устанавливается не отношение большего
или меньшего понятия к третьему понятию,
а устанавливается в одной посылке
отношение большего термина к третьему
понятию («сгорание» в химическом
смысле, т. е. процесс, который не обязательно
сопровождается появлением золы и пепла),
а в другой – отношение меньшего термина
к четвёртому понятию («сгорание» в
повседневном
ненаучном смысле, означающее процесс,
при котором в остатке всегда получаются
зола и пепел). Не удивительно, что, не
будучи связаны между собой через третье
понятие в посылках, больший и меньший
термины не могут оказаться связанными
в выводе.
И здесь основа
ошибки не столько в нарушении правила
о количестве терминов, входящих в
силлогизм, сколько в двусмысленности
слова «сгорание», которое имеет не одно
значение, а два, выражает два понятия.
Ошибка здесь
состоит в том, что посылки, имеющие
строение
M1
— P
S – M2
мы
– вследствие недостаточного различения
M1
от М2
– принимаем за посылки, имеющие строение
обычного силлогизма:
М — Р
S
— M
Ошибки возможны
не только относительно среднего, но
также и относительно большего и меньшего
терминов.
Из сказанного
видим, что ошибки, встречающиеся в
силлогизмах, редко состоят в нарушении
одних лишь правил логической связи
между посылками и терминами. В последнем
счёте основой ошибки вывода обычно
является ложность посылок, которые
принимаются в качестве истинных.
Задачи
1.
Определите, какие из следующих
умозаключений будут силлогизмами и
какие – несиллогистическими умозаключениям.
«Так
как а
больше b,
а b
равное, то, следовательно, а
больше с»
«Монблан ниже Эльбруса, Эльбрус ниже
пика Сталина, следовательно, Монблан
ниже пика Сталина»; «Лермонтов был
предшественником Льва Толстого, Лев
Толстой был современником Чернышевского,
следовательно, Лермонтов был
предшественником Чернышевского»; «Так
как биолог должен «уметь владеть
микроскопом, а Иванов не владеет
микроскопом, то Иванов–не биолог»; «Так
как все равносторонние треугольники
равноугольны и так как треугольник АВС
– равносторонний, то, следовательно,
треугольник АВС
– равноугольный»; «Ботвинник как
шахматист сильнее Смыслова, Смыслов
как шахматист сильнее Рагозина,
следовательно, Ботвинник как шахматист
сильнее Рагозина»; «Ни одна из европейских
гор не выше Эльбруса, Эверест выше
Эльбруса, следовательно, Эверест не
принадлежит к числу европейских гор».
2. Рассмотрев
следующие силлогизмы, определите: а)
правильны они или неправильны с точки
зрения логической связи между посылками
и выводом, б) если они правильны, то по
какой фигуре в них сделан вывод; в) если
они неправильны, то какие из правил,
общих для всех силлогизмов, и какие из
правил, специальных для отдельных фигур,
в них нарушены:
«Все сильные
шахматисты хорошо знают теории шахматной
игры. Николаев – не сильный шахматист,
следовательно, Николаев не знает теории
шахматной игры»; «Все умеющие играть в
хоккей – конькобежцы, Сергеев – не
конькобежец, следовательно, Сергеев не
умеет играть в хоккей»; «Белые ночи
наблюдаются не южнее параллели Полтавы,
Киев находится не южнее параллели
Полтавы, следовательно, в Киеве наблюдаются
белые ночи»; «Некоторые растения
размножаются спорами, все папоротники
– растения, следовательно, все папоротники
размножаются спорами»; «Все
папоротники–споровые, все хвощи–споровые,
следовательно, некоторые хвощи–папоротники»:
«Все герои Советского Союза награждаются
орденом Ленина, товарищ N награждён
орденом Ленина, следовательно, товарищ
N – Герой Советского Союза»; «Тяжёлые
бомбардировщики не бывают одномоторные,
самолёт Михайлова – одномоторный,
следовательно, самолёт Михайлова–не
тяжёлый бомбардировщик»; «Все членистоногие
– беспозвоночные, все пауки –
членистоногие, следовательно, все пауки–
беспозвоночные»; «У всех рек нашего
полушария, текущих с севера на юг, правый
берег гористый, а левый – низменный,
река Днепр – одна из рек нашего полушария,
текущих с севера на юг, следовательно,
правый берег Днепра – гористый, а
левый–низменный»; «Во всех древнеиндийских
рукописях слова не отделяются одно от
другого, в этой рукописи слова не
отделяются одно от другого, следовательно,
эта рукопись – древнеиндийская»;
«Газовые фонтаны являются признаком
близких нефтерождений, в посёлки N забил
газовый фонтан, следовательно, вблизи
посёлка N имеются нефтерождения»; «Все
великие учёные – глубокомысленные
люди, все великие учёные рассеянные
люди, следовательно, некоторые рассеянные
люди–глубокомысленные люди»; «Все
планеты имеют быстрое видимое движение,
ни одна планета–не звезда, следовательно,
некоторые звёзды не имеют быстрого
видимого движения».
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Фигуры силлогизма – это его разновидности, различающиеся положением среднего термина (М) в посылках.
Правильные виды силлогизма (или модусы), распределённые по фигурам
| Фигура 1 | Фигура 2 | Фигура 3 | Фигура 4 |
| AAA | EAE | AAI | AAI |
| EAE | AEE | IAI | AEE |
| AII | EIO | AII | IAI |
| EIO | AOO | EAO | EAO |
| OAO | EIO | ||
| EIO |
Данные модусы необходимо знать наизусть. Для облегчения заучивания придумали следующее стихотворение, написанное гекзаметром:
Фигура 1: Barbara Celarent Darii Ferio
Фигура 2: Cesare Camestres Festino Baroco
Фигура 3: Darapti Disamis Datisi Felapton Bocardo Ferison
Фигура 4: Bramantip Camenes Dimaris Fesapo Fresison
Здесь каждое слово, напечатанное курсивным шрифтом, означает отдельный модус, посылки и заключение которого легко определить, если взять гласные буквы. Например,
- Barbara означает модус фигуры 1, в котором обе посылки и заключение суть ААА;
- Celarent означает модус ЕАЕ.
Посылки изображаются горизонтальными линиями, крайние точки которых обозначают термины, при этом соединяют линией средний термин в разных посылках.
Существует четыре фигуры силлогизма, каждая из которых имеет свои правила.
Во 2-й фигуре средний термин занимает место предиката в обеих посылках.
Например:
Все студенты юрфака (Р) сдают экзамен по логике (M).
Иванов (S) не сдает экзамен по логике (М).
_______________________________________________________________________________
Иванов (S) не является студентом юрфака (P).
Модусы второй фигуры
Cesare
Е Ни один справедливый человек не завистлив.
А Всякий честолюбивый завистлив.
___________________________________________________________
E Ни один честолюбивый человек не есть справедлив.
Camestres
А Преступники действуют из злого намерения.
Е N. не действовал из злого намерения.
__________________________________________________
Е N не есть преступник.
Festino
Е Ни один благоразумный человек не суеверен.
I Некоторые хорошо образованные люди суеверны.
_______________________________________________________________
О Некоторые хорошо образованные люди неблагоразумны.
Baroko
A Все истинно моральные действия совершаются из правильных мотивов.
O Некоторые действия, благодетельные для других, нe совершаются из таких мотивов.
___________________________________________________________________________
О Некоторые благодетельные для других действия не суть истинно моральные.
Правила 2-й фигуры простого категорического силлогизма
-
- Первая (большая) посылка должна быть общей.
- Одна из посылок должна быть отрицательной.
Второе правило фигуры выводится из 2-го правила терминов (средний термин должен быть распределен хотя бы в одной из посылок). Но так как средний термин занимает место предиката в обеих посылках, то одна из них должна быть отрицательным суждением, т.е. суждением с распределенным предикатом.
Если одна из посылок — отрицательное суждение, то и заключение должно быть отрицательным (суждение с распределенным предикатом). Но в этом случае предикат заключения (больший термин) должен быть распределен и в большей посылке, где он занимает место субъекта суждения. Такой посылкой должно быть общее суждение, в котором субъект распределен. Значит, большая посылка должна быть общим суждением.
Правила 2-й фигуры исключают сочетания посылок АА, IA, ОА, IE, AI, оставляя модусы ЕАЕ, AEE, ЕIO, АОО, которые показывают, что эта фигура дает только отрицательные заключения.
Например:
Все физики стремятся к истине.
Некоторые историки стремятся к истине.
______________________________________________________
Некоторые историки являются физиками?
Вывод ложный, поскольку нарушено правило второй фигуры – обе посылки утвердительные суждения.
Другой пример:
Некоторые люди могут быть отцами.
Ни одна женщина не может быть отцом.
___________________________________________________________
Некоторые женщины не могут быть людьми?
Вывод ложный, поскольку нарушено первое правило второй фигуры – первая посылка частное суждение.
Роль второй фигуры простого категорического силлогизма в познании
2-я фигура применяется, когда необходимо показать, что отдельный случай (конкретное лицо, факт, явление) не может быть подведен под общее положение. Этот случай исключается из числа предметов, о которых сказано в большей посылке.
В судебной практике 2-я фигура используется
-
- для заключений об отсутствии состава преступления в данном конкретном случае,
- для опровержения положений, противоречащих тому, о чем говорится в посылке, выражающей общее положение.
Например:
Подстрекателем (Р) признается лицо, склонившее другое лицо к совершению преступления (М).
H.(S) не признается лицом, склонившим другое лицо
к совершению преступления (М).
_____________________________________________________
H.(S) не является прдстрекателем (Р)
Задачи, решаемые при помощи силлогизмов:
1. Применение общих положений (аксиом, законов природы, правoвых норм) к частным случаям.
Эту задачу решают силлогизмы по первой фигуре.
Например:
Все студенты сдают экзамены.
Вы — студенты.
_________________________________________
Вы сдаете экзамены.
2. Опровержение неправильных дедукций или неправильных подчинений.
Данная задача противоположна первой задаче и силлогизмы, используемые для ее решения, часто используются для опровержения неправильных выводов, сделанных по первой фигуре, когда происходит исключение частного случая из общего правила (по второй фигуре).
Например:
Этот удар мог быть нанесен человеком большой физической силы.
Обвиняемый не обладает большой физической силой.
____________________________________________________________________
Обвиняемый не мог нанести этот удар.
3. Обоснование исключений из общих положений.
Эта ситуация часто встречается в споре. Предположим, ваш оппонент выдвигает какое-либо общее положение, а вам надо доказать исключение из него. Тогда можно прибегнуть к 3-й фигуре.
Например, надо доказать, что суждение «Все люди имеют преступные наклонности» является ложным. Для этого надо построить силлогизм по 3-й фигуре:
Ни один ребенок не имеет преступных наклонностей.
Каждый ребенок является человеком.
___________________________________________________________________
Следовательно, некоторые люди не имеют преступных наклонностей.

Мы с вами сосредоточимся только на силлогизмах. Они отличаются тем, что и в посылках и в заключении имеют категорические атрибутивные высказывания и на основании наличия или отсутствия каких-то свойств у объектов позволяют сделать вывод о наличии или отсутствии у них других свойств.
Содержание:
- Простой категорический силлогизм
- Правила терминов
- Задачи Эйнштейна
- Энтимемы
- Сориты
- Упражнения
- Проверочные вопросы на усвоение материала
Простой категорический силлогизм
Простой категорический силлогизм – это одно из наиболее простых и часто встречающихся умозаключений. Он состоит из двух посылок. В первой посылке говорится об отношении терминов А и В, во второй – об отношениях терминов В и С. На основании этого делается вывод об отношении терминов А и С. Такой вывод возможен потому, что обе посылки содержат общий термин В, который опосредует отношение между терминами А и С.
Приведём пример:
- Все рыбы не могут жить без воды.
- Все акулы – это рыбы.
- Следовательно, все акулы не могут жить без воды.
В данном случае, термин «рыбы» – это общий термин для двух посылок, и он помогает связать термины «акулы» и «существа, способные жить без воды». Общий термин для двух посылок принято называть средним термином. Субъект заключения (в нашем примере это «акулы») называют меньшим термином. Предикат заключения («существа, способные жить без воды») называют бóльшим термином. Соответственно, посылку, содержащую меньший термин, называют меньшей посылкой («Все акулы – это рыбы»), а посылку, содержащую больший термин, – бóльшей посылкой («Все рыбы не могут жить без воды»).
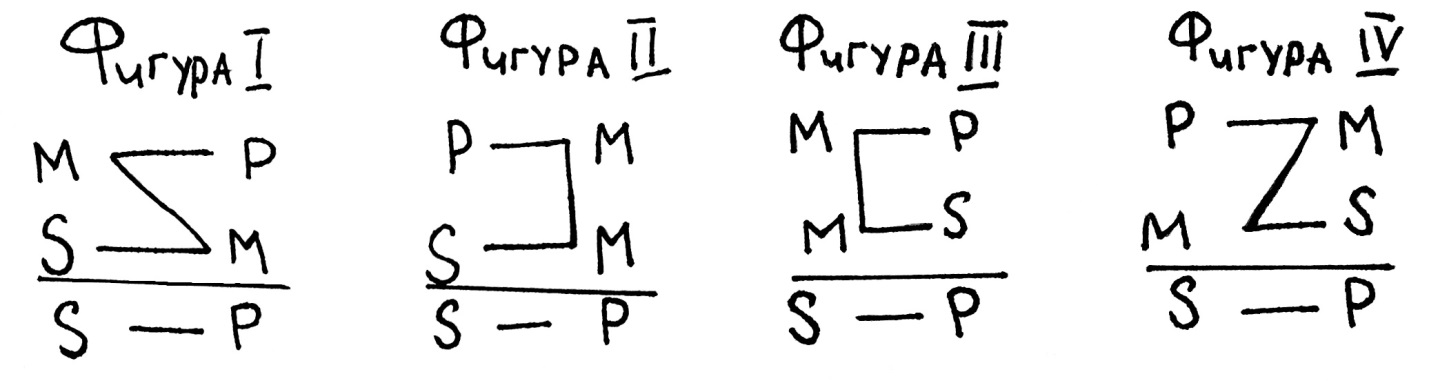
Фигура – это форма простого категорического силлогизма, которая определяется расположением среднего термина.
Сверху расположена большая посылка, за ней следует меньшая посылка, под чертой находится заключение. Буквой S обозначен меньший термин, буквой P – больший термин, буквой М – средний термин.
Далее, фигуры могут наполняться разным содержанием, то есть на место посылок и заключений могут подставляться разные типы категорических атрибутивных высказываний. Например:
- Всякий М есть P
- Всякий S есть М
- Всякий S есть P
или:
- Ни один М не есть P
- Некоторые М есть S
- Некоторые S не есть P
Эти различные сочетания высказываний в фигурах образуют так называемые модусы. Каждая фигура имеет 64 модуса, таким образом, на все четыре фигуры приходятся всего 256 модусов. Если подумать обо всём многообразии умозаключений, имеющих форму силлогизмов, то 256 модусов – это не так уж и много. Кроме того, далеко не все модусы образуют правильные умозаключения, то есть существуют такие модусы, которые при истинности посылок не гарантируют истинности умозаключения. Такие модусы называются неправильными. Правильными же называются те модусы, с помощью которых из истинных посылок мы всегда получаем истинное заключение. Всего существует 24 правильных модуса – по шесть на каждую фигуру. Это означает, что во всей классической силлогистике, которая исчерпывает львиную долю рассуждений, производимых людьми, существует всего 24 вида правильных умозаключений. Это очень маленькое число, поэтому правильные модусы не так уж и сложно запомнить.
Каждый из этих модусов ещё в Средние века получил особое мнемоническое наименование. Каждый тип категорического атрибутивного высказывания был обозначен с помощью всего одной буквы. Высказывания типа «Все S есть P» обозначили буквой «а», первой буквой в латинском слове «affirmo» («утверждаю»), и их запись превратилась в «SaP». Высказывания вида «Некоторые S есть P» записывались с помощью буквы «i», второй гласной в слове «affirmо», поэтому они выглядели как «SiP». Высказывания формы «Ни один S не есть P» обозначили буквой «е», первой гласной в латинском слове «nego» («отрицаю»), их стали записывать в виде «SeP». Как вы, наверное, уже догадались высказывания типа «Некоторые S не есть P» обозначили буквой «о», второй гласной в слове «nego», их формальная запись выглядела как «SoP». Поэтому модусы правильных силлогизмов традиционно обозначаются именно с помощью этих четырёх букв, которые для удобства запоминания представлены в виде слов. Таблица всех правильных модусов выглядит так:
|
Фигура I |
Фигура II |
Фигура III |
Фигура IV |
|
Barbara (aaa) Celarent (eae) Darii (aii) Ferio (eio) Barbari (aai) Celaront (eao) |
Baroko (aoo) Cesare (eae) Camestres (aee) Festino (eio) Camestrop (aeo) Cesaro (eao) |
Bocardo (oao) Disamis (iai) Datisi (aii) Ferison (eio) Darapti (aai) Felapton (eao) |
Camenos (aeo) Dimaris (iai) Camenes (aee) Fresison (eio) Bramantip (aai) Fesapo (eao) |
К примеру, модус второй фигуры Cesare (eae) в развёрнутом виде будет выглядеть так:
- Ни один P не есть М
- Все S есть М
- Ни один S не есть P
Хотя 24 модуса – это совсем не много и в таблице можно усмотреть некоторые регулярности (например, для всех фигур верны модусы eao и eio), запомнить её всё равно сложно. К счастью, это совсем и необязательно. Для проверки силлогизмов можно также пользоваться модельными схемами. Только в отличие от тех схем, которые мы строили раньше, на них уже должно присутствовать не два, а три термина: S, P, M.
Давайте возьмём модус четвёртой фигуры Bramantip (aai) и проверим его с помощью модельных схем.
- Всякий P есть М
- Всякий М есть S
- Некоторые S есть P
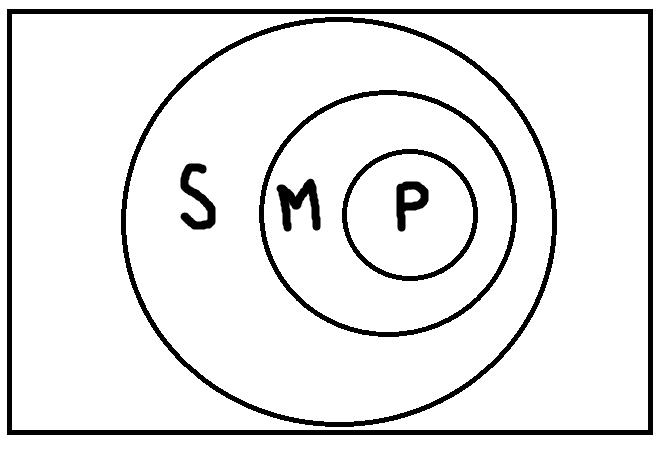
Сначала нужно найти такие модельные схемы, при которых обе посылки будут одновременно истинными. Таких схем всего четыре:
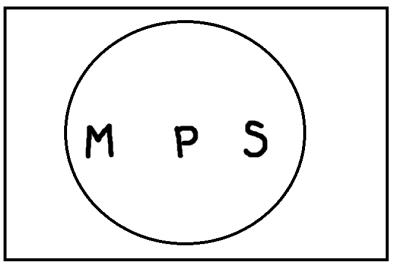
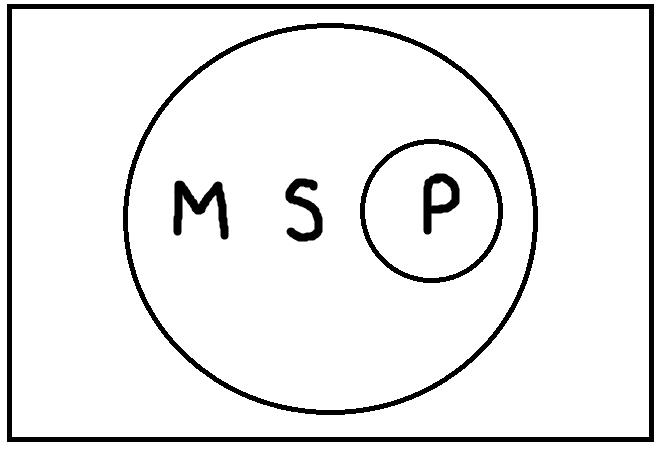
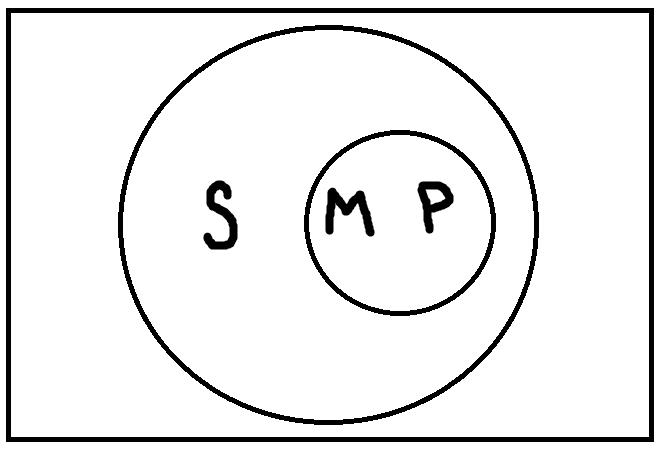
Теперь на каждой из этих схем мы должны проверить, верно ли будет высказывание «Некоторые S есть P», представляющее заключение. В результате проверки, мы обнаруживаем, что на каждой схеме это высказывание будет верным. Таким образом, умозаключение по модусу Bramantip (aai) четвёртой фигуры правильное. Если бы была хотя бы одна схема, на которой это высказывание было бы ложным, то умозаключение было бы неправильным.
Метод проверки силлогизмов с помощью модельных схем хорош, так как он позволяет представить отношения между терминами наглядно. Однако для некоторых посылок могут оказаться верными очень много схем сразу. В результате их построение и проверка будут представлять собой трудоёмкую и отнимающую много времени задачу. Таким образом, метод модельных схем не всегда удобен.
Поэтому логики разработали ещё один метод для определения, правильный силлогизм или нет. Этот метод называется синтаксическим и представляет собой два перечня правил (правила терминов и правила посылок), при соблюдении которых силлогизм будет верным.
Модус простого категорического силлогизма является правильным, если он удовлетворяет следующим условиям:
Правила терминов
- Простой категорический силлогизм должен включать только три термина.
- Средний термин должен быть распределён хотя бы в одной из посылок.
- Если больший или меньший термин не распределён в посылке, то он должен быть нераспределён и в заключении.
Правила посылок:
- Хотя бы одна из посылок должна быть утвердительной.
- Если обе посылки являются утвердительными, то и заключение должно быть утвердительным.
- Если одна из посылок отрицательная, то и заключение должно быть отрицательным.
Правила посылок понятны, а правила терминов требуют некоторых пояснений. Начнём с правила о трёх терминах. Хотя оно кажется очевидным, оно довольно часто нарушается вследствие так называемой подмены терминов. Посмотрите на следующий силлогизм:
- Золото – элемент 11 группы, шестого периода периодической системы химических элементов Д. И. Менделеева, с атомным номером 79.
- Молчание – золото.
- Молчание – элемент 11 группы, шестого периода периодической системы химических элементов Д. И. Менделеева, с атомным номером 79.
Прежде всего, если вы помните фигуры и правильные модусы, вы сразу можете сказать, что этот силлогизм неправильный, так как он относится ко второй фигуре и имеет модус aaa, который не принадлежит к списку правильных модусов для этой фигуры. Но если вы их не помните, всё равно вы можете выявить его ложность, потому что здесь явно присутствует четыре термина, вместо трёх. Термин «золото» употребляется в двух совершенно различных смыслах: как химический элемент и как нечто, обладающее ценностью. Посмотрим на более сложный пример:
- Все книги из собрания Российской государственной библиотеки нельзя прочитать за целую жизнь.
- «Отцы и дети» Ивана Тургенева – книга из собрания Российской государственной библиотеки.
- «Отцы и дети» Ивана Тургенева нельзя прочитать за целую жизнь.
Кажется, что этот силлогизм соответствует модусу Barbara первой фигуры. Однако посылки истинны, а заключение ложно.
Если бы мы заменили слово «все» на слова «каждый в отдельности», то первая посылка попросту стала бы ложной: «Каждую в отдельности книгу из собрания Российской государственной библиотеки нельзя прочитать за целую жизнь». Таким образом, мы получаем четыре термина вместо трёх, а потому это умозаключение ложно.
Теперь перейдём к правилам о распределённости терминов. Для начала объясним, что это за характеристика. Термин называют распределённым, если в высказывании речь идёт обо всех объектах, входящих в его объём. Соответственно, термин не распределён, если в высказывании речь идёт не обо всех объектах, составляющих его объём. Грубо говоря, термин распределён, если мы говорим обо всех предметах, и не распределён, если мы говорим только о некоторых предметах, о части объёма термина.
Давайте возьмём типы высказываний и посмотрим, какие термины в них распределены, а какие нет. Распределённый термин отмечается знаком «+», нераспределённый – знаком «–».
Все S+ есть P–.
Ни один S+ не есть P+.
Некоторые S– есть P–.
Некоторые S– не есть P+.
а+ есть P–.
a+ не есть P+.
Как видно, субъект всегда распределён в общих и единичных высказываниях, но не распределён в частных. Предикат всегда распределён в отрицательных высказываниях, но не распределён в утвердительных. Если теперь перенести это на наши правила для терминов, то получается, что средний термин хотя бы в одной из посылок должен быть взят во всём своём объёме.
- Пингвины – это птицы.
- Некоторые птицы не умеют летать.
- Пингвины не умеют летать.
Хотя и высказывания над чертой и высказывание под чертой истинны, умозаключение как таковое здесь отсутствует. Здесь нет логического перехода от посылок к заключению. И это можно легко выявить, так как средний термин «птицы» ни разу не берётся во всём своём объёме.
Что касается третьего правила терминов, если в посылках речь идёт только о части объектов из объёма терминов, то в заключении мы не можем ничего утверждать обо всех объектах объёма терминов. Мы не можем перейти от части к целому. Кстати, обратный переход возможен: если мы говорим обо всех элементах объёма терминов, то мы можем сделать заключение о части из них.
Задачи Эйнштейна
Эта игра является нашей версией всемирно известной «загадки Эйнштейна», в которой 5 иностранцев живут на 5 улицах, едят 5 видов еды и т.д. Подробнее про эту задачу написано здесь. В подобных заданиях вам нужно сделать правильное умозаключение на основе имеющихся посылок, которых, на первый взгляд, для этого недостаточно.
Энтимемы
Во время реальных дискуссий и споров мы довольно часто опускаем те или иные части рассуждения. Это приводит к возникновению энтимем. Энтимема – это сокращённая форма умозаключения, в которой пропущены посылки или заключение. Важно не путать энтимемы с однопосылочными умозаключениями. Энтимема – это именно многопосылочное умозаключение, просто его части в силу тех или иных причин опущены. Иногда такие пропуски оправданы, так как оба собеседника хорошо разбираются в проблеме, и им нет нужды проговаривать все шаги. Между тем, недобросовестные собеседники могут специально пользоваться энтимемами, чтобы затемнить и запутать своё рассуждение и скрыть свои истинные аргументы или выводы. Поэтому необходимо уметь отличать корректные энтимемы от некорректных. Энтимема называется корректной, если она может быть восстановлена в виде правильного модуса категорического силлогизма, и если все пропущенные посылки оказываются истинными.
Поговорим о том, как восстановить энтимему до полного силлогизма. В первую очередь нужно понять, что именно пропущено. Для этого нужно обратить внимание на слова-маркеры, обозначающие причинно-следственные связи: «таким образом», «следовательно», «так как», «потому что», «в результате» и т.д. К примеру, возьмём рассуждение: «Золото – это драгоценный металл, потому что оно практически не окисляется на воздухе». Здесь заключением является высказывание «Золото – это драгоценный металл». Одна из посылок: «Золото практически не окисляется на воздухе». Ещё одна посылка пропущена. Нужно сказать, что чаще всего пропускают именно одну из посылок. Довольно странно, если в рассуждении отсутствует самое важное – вывод.
Итак, мы установили, что именно пропущено. В нашем примере – это посылка. Большая это посылка или меньшая? Как вы помните, меньшая посылка содержит субъект заключения («золото»), а большая – предикат заключения («драгоценный металл»). Посылка, содержащая субъект заключения нам уже известна: «Золото практически не окисляется на воздухе». Значит, нам известна меньшая посылка, и не известна большая. Кроме того, благодаря известной посылке, мы можем установить и средний термин: «металлы, которые практически не окисляются на воздухе», – тот термин, который не содержится в заключении.
Теперь располагаем известную нам информацию в форме силлогизма:
- 1.
- 2. Золото практически не окисляется на воздухе.
- 3. Золото – это драгоценный металл.
Или в виде схемы:
- 1.
- 2. SaМ
- 3. SaP
В большей посылке должны находиться предикат заключения и средний термин: «драгоценные металлы» (P) и «металлы, которые окисляются на воздухе» (M). Здесь возможны два варианта:
- 1. P M
- 2. SaМ
- 3. SaP
Или:
- 1. М P
- 2. SaМ
- 3. SaP
Значит, возможен силлогизм либо второй фигуры, либо первой фигуры. Теперь смотрим на нашу табличку с правильными модусами силлогизмов. Во второй фигуре вообще нет правильных модусов, где в заключении стояло бы высказывание типа а. В первой фигуре есть только один такой модус – Barbara. Достраиваем наш силлогизм:
- 1. МаP
- 2. SaМ
- 3. SaP
Или:
- 1. Все металлы, которые практически не окисляются на воздухе, являются драгоценными.
- 2. Золото практически не окисляется на воздухе.
- 3. Золото – драгоценный металл.
Теперь проверяем, истинна ли наша восстановленная посылка. В нашем случае она истинна, поэтому энтимема была правильной.
Сориты
Термином «сориты» пользовался Льюис Кэррол для обозначения сложных силлогизмов, которые имеют более чем две посылки. По большому счёту, сорит представляет собой гибрид силлогизма и энтимемы. Он устроен следующим образом: дано множество посылок, из каждой пары посылок делаются промежуточные выводы, которые обычно опускаются, к промежуточным выводам присоединяются новые посылки, из них делаются новые промежуточные выводы, к которым опять присоединяются новые посылки и так далее, пока мы не переберём все имеющиеся посылки и не дойдём до окончательного заключения. В принципе подобным образом люди и рассуждают в повседневной жизни. Поэтому очень важно уметь решать сориты и оценивать, правильны они или нет.
Мы приведём пример сорита из книги Льюиса Кэррола «История с узелками»:
1. Все полисмены из нашей округи ужинают у нашей кухарки.
2. Человек с длинными волосами не может не быть поэтом.
3. Амос Джадд никогда не сидел в тюрьме.
4. Все кузены нашей кухарки любят холодную баранину.
5. В этой округе нет других поэтов, кроме полисменов.
6. С нашей кухаркой не ужинает никто, кроме её кузенов.
7. Все люди с короткими волосами сидели в тюрьме.
8. Амос Джадд любит холодную баранину.
Над чертой находятся посылки, под чертой – заключение.
Как же нужно решать и проверять сориты? Дадим пошаговую инструкцию. Во-первых, необходимо привести все посылки в более или менее стандартную форму:
1. Все полисмены из нашей округи ужинают у нашей кухарки.
2. Все люди с длинными волосами являются поэтами.
3. Амос Джадд не сидел в тюрьме.
4. Все кузены нашей кухарки любят холодную баранину.
5. Все поэты из нашего округа являются полисменами.
6. Все люди, ужинающие с нашей кухаркой, приходятся ей кузенами.
7. Все люди с короткими волосами сидели в тюрьме.
Теперь нужно взять две исходные посылки. По большому счёту, неважно, с каких именно посылок вы начнёте. Главное, чтобы ваши исходные посылки вместе содержали всего три термина. Это означает, что мы не можем взять посылки «Амос Джадд не сидел в тюрьме» и «Все кузены нашей кухарки любят холодную баранину». В них входят четыре разных термина, а потому мы не можем сделать из них никакого заключения. Я в качестве исходных возьму посылки 7 и 3 и сделаю из них вывод по правилам для простых категорических силлогизмов.
- 1. Все люди с короткими волосами сидели в тюрьме.
- 2. Амос Джадд не сидел в тюрьме.
- 3. Амос Джадд не является человеком с короткими волосами.
Этот силлогизм соответствует модусу Camestres (aee) второй фигуры. Теперь для удобства я переформулирую наш промежуточный вывод следующим образом: «Амос Джадд является человеком с длинными волосами». Этот промежуточный вывод я соединяю с посылкой номер 2:
- 1. Все люди с длинными волосами являются поэтами.
- 2. Амос Джадд является человеком с длинными волосами.
- 3. Амос Джадд является поэтом.
Этот силлогизм соответствует модусу Barbara (aaa) первой фигуры. Теперь я присоединяю этот промежуточный вывод к посылке номер 5:
- 1. Все поэты из нашего округа являются полисменами.
- 2. Амос Джадд является поэтом.
- 3. Амос Джадд является полисменом.
Этот силлогизм опять же соответствует модусу Barbara (aaa) первой фигуры. Присоединяем промежуточный вывод к посылке номер 1:
- 1. Все полисмены из нашей округи ужинают у нашей кухарки.
- 2. Амос Джадд является полисменом.
- 3. Амос Джадд ужинает у нашей кухарки.
Это силлогизм, как вы уже, наверное, заметили, тоже представляет собой модус Barbara (aaa) первой фигуры. Присоединяем этот вывод к посылке номер 6:
- 1. Все люди, ужинающие с нашей кухаркой, приходятся ей кузенами.
- 2. Амос Джадд ужинает у нашей кухарки.
- 3. Амос Джадд приходится кузеном нашей кухарке.
Опять Barbara, которая является одним из самых распространённых модусов. Присоединяем к нашему последнему промежуточному выводу последнюю посылку номер 4:
- 1. Все кузены нашей кухарки любят холодную баранину.
- 2. Амос Джадд приходится кузеном нашей кухарке.
- 3. Амос Джадд любит холодную баранину.
Итак, с помощью всё того же модуса Barbara мы получили наше заключение: «Амос Джадд любит холодную баранину». Таким образом, сориты решаются и проверяются с помощью пошагового разделения на простые категорические силлогизмы. В нашем примере сорит оказался правильным, но возможны и обратные ситуации. Существует два условия корректности соритов. Во-первых, каждый сорит должен разбиваться на последовательность правильных модусов силлогизмов. Во-вторых, заключение, которое вы получаете, когда все посылки исчерпаны, должно совпасть с заключением сорита. Это условие действует в тех случаях, когда вы имеете дело с чужим рассуждением, в котором уже присутствует какое-то заключение.
Итак, мы рассмотрели различные многопосылочные умозаключения на примере простых категорических силлогизмов, энтимем и соритов. По большому счёту, если вы знаете, как иметь с ними дело, то вы вооружены для любых дискуссий с любыми противниками. Единственное, что может на данный момент вызывать некоторое недовольство, это необходимость тратить много времени на проверку правильности умозаключений. Не стоит расстраиваться по этому поводу: лучше выглядеть тугодумом, который рассуждает правильно, чем блестящим демагогом, который не замечает своих и чужих ошибок. Тем более, с накоплением опыта внимательного отношения к умозаключениям у вас появится чутьё, автоматический навык, позволяющий быстро отделять корректные рассуждения от некорректных. Поэтому упражнений к этому уроку будет много, чтобы у вас была возможность набить руку.
Упражнения
Упражнения 1, 2 и 3 взяты из книги Льюиса Кэррола «История с узелками», М.: Мир, 1973.
Упражнение 1
Сделайте заключения из следующих посылок по правилам для простого категорического силлогизма. Помните, что простой категорический силлогизм должен содержать только три термина. Не забывайте приводить высказывания к стандартному виду.
1
- Зонтик – очень нужная вещь в путешествии.
- Отправляясь в путешествие, всё лишнее следует оставлять дома.
- ?
2
- Музыка, которую можно услышать, вызывает колебания воздуха.
- Музыка, которую нельзя услышать, не стоит того, чтобы за неё платили деньги.
- ?
3
- Ни один француз не любит пудинга.
- Все англичане любят пудинг.
- ?
4
- Ни один старый скряга не жизнерадостен.
- Некоторые старые скряги тощи.
- ?
5
- Все непрожорливые кролики чёрные.
- Ни один старый кролик не склонен к воздержанию в пище.
- ?
6
- Ничто разумное никогда не ставило меня в тупик.
- Логика ставит меня в тупик.
- ?
7
- Ни в одной из исследованных до сих пор стран не обитают драконы.
- Неисследованные страны пленяют воображение.
- ?
8
- Некоторые сны ужасны.
- Ни один барашек не внушает ужаса.
- ?
9
- Ни одному лысому созданию не нужна расчёска.
- Ни у одной ящерицы нет волос.
- ?
10
- Все яйца можно разбить.
- Некоторые яйца сварены вкрутую.
- ?
Упражнение 2
Проверьте, правильны ли следующие рассуждения. Попробуйте разные способы проверки. Не забывайте ставить большую посылку на первую строку.
1
- Словари полезны.
- Полезные книги высоко ценятся.
- Словари высоко ценятся.
2
- Золото тяжёлое.
- Ничто, кроме золота, не сможет заставить его замолчать.
- Ничто лёгкое не сможет заставить его замолчать.
3
- Некоторые галстуки безвкусны.
- Всё, сделанное со вкусом, приводит меня в восторг.
- Я не в восторге от некоторых галстуков.
4
- Ни одно ископаемое животное не может быть несчастно в любви.
- Устрица может быть несчастна в любви.
- Устрицы – не ископаемые животные.
5
- Ни одна горячая сдоба не полезна.
- Все булочки с изюмом неполезны.
- Булочки с изюмом – не сдоба.
6
- Некоторые подушки мягкие.
- Ни одна кочерга не мягкая.
- Некоторые кочерги – не подушки.
7
- Скучные люди невыносимы.
- Ни одного скучного человека не упрашивают остаться, когда он собирается уходить из гостей.
- Ни одного невыносимого человека не упрашивают остаться, когда он собирается уходить из гостей.
8
- Ни одна лягушка не имеет поэтической внешности.
- Некоторые утки выглядят прозаично.
- Некоторые утки – не лягушки.
9
- Все разумные люди ходят ногами.
- Все неразумные люди ходят на голове.
- Ни один человек не ходит на голове и ногах.
Упражнение 3
Найдите заключения следующих соритов.
1
- Малые дети неразумны.
- Тот, кто может укрощать крокодилов, заслуживает уважения.
- Неразумные люди не заслуживают уважения.
2
- Ни одна утка не танцует вальс.
- Ни один офицер не откажется потанцевать вальс.
- У меня нет другой птицы, кроме уток.
3
- Всякий, кто находится в здравом уме, может заниматься логикой.
- Ни один лунатик не может быть присяжным заседателем.
- Ни один из ваших сыновей не может заниматься логикой.
4
- В этой коробке нет моих карандашей.
- Ни один из моих леденцов – не сигара.
- Вся моя собственность, не находящаяся в этой коробке, состоит из сигар.
5
- Ни один терьер не блуждает среди знаков Зодиака.
- То, что не блуждает среди знаков Зодиака, не может быть кометой.
- Только у терьера хвост колечком.
6
- Никто не станет выписывать газету «Таймс», если он не получил хорошего образования.
- Ни один дикобраз не умеет читать.
- Те, кто не умеет читать, не получили хорошего образования.
7
- Никто их тех, кто действительно ценит Бетховена, не станет шуметь во время исполнения «Лунной сонаты».
- Морские свинки безнадёжно невежественны в музыке.
- Те, кто безнадёжно невежественен в музыке, не станут соблюдать тишину во время исполнения «Лунной сонаты».
8
- Вещи, продаваемые на улице, не имеют особой ценности.
- Только дрянь можно купить за грош.
- Яйца большой гагарки представляют большую ценность.
- Лишь то, что продаётся на улице, и есть настоящая дрянь.
9
- Те, кто нарушает свои обещания, не заслуживают доверия.
- Любители выпить очень общительны.
- Человек, выполняющий свои обещания, честен.
- Ни один трезвенник не ростовщик.
- Тому, кто очень общителен, всегда можно верить.
10
- Любая мысль, которую нельзя выразить в виде силлогизма, поистине смешна.
- Моя мечта о сдобных булочках не стоит того, чтобы её записывать на бумаге.
- Ни одну мою несбыточную мечту нельзя выразить в виде силлогизма.
- Мне не приходило в голову ни одной действительно смешной мысли, о которой я бы не сообщим своему другу.
- Я только и мечтаю, что о сдобных булочках.
- Я никогда не высказывал своему другу ни одной мысли, если она не стоила того, чтобы её записать на бумаге.
Упражнение 4
Проверьте правильность следующих энтимем.
- Барсик – не законопослушный кот, потому что он украл у меня сосиску.
- Ртуть жидкая, следовательно, она не может быть металлом.
- Ни один послушный ребёнок не устраивает истерик по пустякам. Поэтому Толя – непослушный ребёнок.
- Некоторые женщины глупы, значит, некоторые мужчины могут этим воспользоваться.
- Все девушки хотят выйти замуж, так как каждая из них мечтает о пышном белом платье.
- Ни один студент не хочет получить двойку на экзамене, вот почему все студенты – ботаники.
- Некто украл у меня кошелёк, поэтому у меня совсем не осталось денег.
- Павлины – самовлюблённые птицы, потому что у них большой красивый хвост.
Проверьте свои знания
Если вы хотите проверить свои знания по теме данного урока, можете пройти небольшой тест, состоящий из нескольких вопросов. В каждом вопросе правильным может быть только 1 вариант. После выбора вами одного из вариантов, система автоматически переходит к следующему вопросу. На получаемые вами баллы влияет правильность ваших ответов и затраченное на прохождение время. Обратите внимание, что вопросы каждый раз разные, а варианты перемешиваются.
← 6 Умозаключения8 Типы рассуждений →
Логические ошибки, встречающиеся в силлогизмах
§ 52. Некоторые из логических ошибок неправильного вывода, особенно часто встречающиеся в практике мышления, заслуживают быть особо отмеченными.
Одна из наиболее частых здесь ошибок состоит в том, что, умозаключая по первой фигуре, делают вывод при отрицательной меньшей посылке.
Все студенты обязаны держать экзамены.
Аспиранты — не студенты.
——————————————
Аспиранты не обязаны держать экзамены.
Вывод явно ошибочный. Отрицательным вывод может быть лишь при условии, если больший термин будет распределён в большей посылке. Но в большей посылке он, как сказуемое утвердительного суждения, выражающего подчинение понятия S понятию Р, не распределён. Поэтому вывод здесь логически невозможен.
Но если он логически невозможен, то почему же подобная ошибка возможна фактически? — Одним из её источников является неправильное истолкование смысла большей посылки. Если, услышав, что «все студенты обязаны держать экзамены», мы истолкуем это положение в том смысле, будто «одни лишь студенты обязаны держать экзамены», то наш вывод примет следующий вид:
Только студенты обязаны держать экзамены.
Аспиранты — не студенты.
——————————————
Аспиранты не обязаны держать экзамены.
Признав эти посылки истинными, мы сделали из них правильный вывод, т. е. вывод здесь необходимо следует из принятых посылок. Ошибка здесь не в том, что мы игнорировали известное правило о распределённости большего термина, распределённого в выводе, а в том, что, неправильно истолковав смысл большей посылки, мы получили посылку, ложную по существу, а потому получили и ложный вывод.
§ 53. Вторая встречающаяся в практике силлогистических выводов ошибка состоит в том, что делают вывод по второй фигуре из двух утвердительных посылок.
Пример:
Все рыбы имеют плавники.
Это животное имеет плавники.
———————————
Это животное — рыба.
Здесь вывод — явно ошибочный. Так как средний термин в обеих посылках является предикатом утвердительного суждения, выражающего подчинение понятий, то он не распределён ни в одной из посылок. Поэтому никакой вывод здесь невозможен. И «рыбы» и «это животное» входят в объём понятия «животные, имеющие плавники». Но так как из посылок неизвестно, в какую именно часть этого объёма входят «рыбы» и в какую —«это животное», то отношение «этого животного» к «рыбам» остаётся совершенно невыясненным; возможно, что «это животное» и есть «рыба», и возможно, что оно не есть «рыба».
Однако и в подобном случае ошибка обычно состоит не столько в нарушении известного правила о распределённости среднего термина, сколько в неправильном истолковании смысла большей посылки. Кто, услышав суждение «все рыбы имеют плавники», поймёт его в смысле «только рыбы имеют плавники», тот, очевидно, сделает следующий вывод:
Все животные, имеющие плавники, — рыбы.
Это животное имеет плавники.
———————————————
Это животное — рыба.
В этом выводе заключение было бы необходимо истинным, если бы были истинными обе посылки. Но бо?льшая посылка ложна, и потому вывод также ложен.
§ 54. Третья ошибка, часто встречающаяся в практике выводов, называется «учетверением терминов» (quaternio terminorum). Она состоит в том, что делают вывод из двух посылок, в которые входят не три, а четыре термина.
Пример такой ошибки:
Всякое сгорание даёт в остатке золу и пепел.
Всякое окисление есть сгорание.
———————————————
Всякое окисление даёт в остатке золу и пепел.
Так как связь понятий, входящих в вывод, не видна сразу, то она может быть установлена только через третье понятие, отношение которого к большему и меньшему терминам было бы известно из посылок. Но в нашем примере эта связь не может быть установлена: здесь в посылках устанавливается не отношение большего или меньшего понятия к третьему понятию, а устанавливается в одной посылке отношение большего термина к третьему понятию («сгорание» в химическом смысле, т. е. процесс, который не обязательно сопровождается появлением золы и пепла), а в другой — отношение меньшего термина к четвертому понятию («сгорание» в повседневном ненаучном смысле, означающее процесс, при котором в остатке всегда получаются зола и пепел). Не удивительно, что, не будучи связаны между собой через третье понятие в посылках, больший и меньший термины не могут оказаться связанными в выводе.
И здесь основа ошибки не столько в нарушении правила о количестве терминов, входящих в силлогизм, сколько в двусмысленности слова «сгорание», которое имеет не одно значение, а два, выражает два понятия.
Ошибка здесь состоит в том, что посылки, имеющие строение
М
1—Р
S—M
2
мы — вследствие недостаточного различения М1 от М2—принимаем за посылки, имеющие строение обычного силлогизма:
М—Р
S—M
Ошибки возможны не только относительно среднего, но также и относительно большего и меньшего терминов.
Из сказанного видим, что ошибки, встречающиеся в силлогизмах, редко состоят в нарушении одних лишь правил логической связи между посылками и терминами. В последнем счёте основой ошибки вывода обычно является ложность посылок, которые принимаются в качестве истинных.
Возможные сочетания суждений в силлогизме. В предыдущей главе мы рассмотрели условия правильности силлогизмов. Рассмотрим теперь на примерах приложение этих правил. Мы будем брать по три суждения, которые могли бы составить силлогизм. Эти суждения должны быть или A, или I, или O, или E. Причём само собой разумеется, что для образования силлогизма они могут комбинироваться самыми различными способами. Например, мы могли бы иметь сочетание суждений AAO, EAI и т.п. Но мы должны исследовать, пользуясь вышеизложенными правилами, какие из этих сочетаний или соединений дают правильные силлогизмы.
Для того чтобы решить вопрос, какие сочетания дают правильные силлогизмы, мы должны предварительно решить вопрос, какие вообще возможны сочетания. Для этого мы поступим следующим образом. Возьмём сочетания AA, AE, AI, AO 4 раза и прибавим к этим сочетаниям A, E, I, O, получим:
AAA AEA AIA AOA
AAE AEE AIE AOE
AAI AEI AII AOI
AAO AEO AIO AOO и т.д;
Действуя аналогичным способом, мы можем получить 64 возможных сочетания.
Составив полную таблицу таких сочетаний, мы рассмотрим, руководясь правилами, приведёнными в прошлой главе, какие из этих сочетаний должны быть отброшены, как не соответствующие этим правилам, и какие из этих сочетаний должны быть оставлены, как дающие правильные силлогизмы.
Берём первое сочетание AAA. Это сочетание не противоречит всем восьми правилам.
Сочетание AAE противно правилу 6, потому что в заключении находится отрицательное суждение E; а чтобы это было возможно, нужно, чтобы одна из посылок была суждением отрицательным, между тем в нашем силлогизме AAE обе посылки положительные. Следовательно, данное сочетание оказывается не возможным.
Сочетание AAO противоречит правилу 6, потому что заключение отрицательное, в то время как посылки утвердительные.
Если таким способом исследовать все 64 случая, то останется только 11 сочетаний, которые дают правильные силлогизмы. Эти сочетания следующие: AAA, AAI, AEE, AEO, AII, AOO, EAE, EAO, EIO, IAI, OAO.
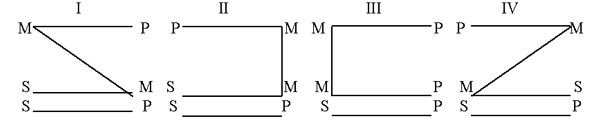
Мы поставили своей задачей решение вопроса, сочетание каких суждений может давать правильные силлогизмы. Казалось бы, что указанным способом мы разрешаем тот вопрос, который нас интересует, но в действительности это не так, потому что при составлении этих сочетаний нужно принять в соображение ещё положение среднего термина в посылках. В том силлогизме, который мы до сих пор рассматривали, средний термин в большей посылке является подлежащим, а в меньшей посылке – сказуемым. Но среднему термину мы можем придавать произвольное положение: мы можем средний термин сделать сказуемым в обеих посылках, или подлежащим в обеих посылках, или, наконец, сказуемым в большей посылке и подлежащим в меньшей. Сообразно с этим мы получаем так называемые четыре фигуры силлогизма, которые и изображены на прилагаемой схеме.
Эта схема даёт возможность помнить положение среднего термина. Горизонтальные линии соединяют посылки, а наклонные и вертикальные линии соединяют средний термин в обеих посылках. Если обратить внимание на то, что наклонные и вертикальные линии, соединяющие средний термин, расположены симметрично, то легко помнить положение среднего термина.
Фигуры и модусы силлогизма. В фигуре 1 средний термин является подлежащим в большей посылке, сказуемым – в меньшей. В фигуре 2 он является сказуемым в большей посылке, сказуемым же и в меньшей посылке. В фигуре 3 он является подлежащим и в большей и в меньшей посылке, и, наконец, в фигуре 4 он является сказуемым в большей посылке и подлежащим – в меньшей.
Теперь мы возьмём 11 возможных сочетаний и предположим, что каждое сочетание изменяет положение среднего термина указанными четырьмя способами, тогда получится 44 сочетание.
Рассмотрим, какие из них возможны. Чтобы показать, как производится такого рода исследование, возьмём для примера сочетание AEE, изобразим его по первой фигуре.
A: Все M суть P.
E: Ни одно S не есть M.
E: Ни одно S не есть P.
Если мы обратим внимание на термин P, то окажется, что в большей посылке как сказуемое обще-утвердительного суждения он не распределён, между тем в заключении как сказуемое обще-отрицательного суждения он распределён. Это противоречит правилу 4, а следовательно, такое сочетание невозможно. Рассмотрим далее, какой вид может принять это сочетание по фигуре 2:
A: все M суть P
E: ни одно M не есть S
E: ни одно S не есть P
Здесь нет нарушения правил силлогизма, а потому заключение правильно. Но если это заключение мы рассмотрим по фигуре 3, то заключение будет нарушать правило 4. Силлогизм примет такой вид:
A: Все M суть P.
E: Ни одно M не есть S.
E: Ни одно S не есть P.
По фигуре 4 это сочетание будет правильно.
Если мы указанным только что способом исследуем все 44 сочетания, то получим следующие 19 правильных видов силлогизма, или модусов, распределённых по фигурам:
Всякий изучающий логику должен все эти модусы знать наизусть. Для облегчения же заучивания придумали следующее стихотворение, написанное гекзаметром:
Barbara , Celarent , Darii , Ferioque prioris;
Cesare , Camestres , Festino , Baroko , sekundae;
Tertia Darapti , Disamis , Datisi , Felapton , Bokardo , Ferison habet;
Quarta insuper addit Bramantip , Camenes , Dimaris , Fesapo , Fresison .
Здесь каждое слово, напечатанное курсивным шрифтом, означает отдельный модус, посылки и заключение которого легко определить, если взять гласные буквы. Например, Barbara означает модус фигуры 1, в котором обе посылки и заключение суть AAA; Celarent означает модус EAE. Значение остальных букв этих слов будет изложено в следующей главе.
Если бы учащийся сам захотел по указанному выше способу определить, какие сочетания суждений дают правильные силлогизмы, то он может воспользоваться след. указаниями.
Если он, руководясь правилами гл. XIII-й, станет отбрасывать те сочетания, которые противоречат правилам, то у него должно остаться след. 12 сочетаний: AAA AAI AEE AEO AII AOO EAE EAO EIO IAI OAO. Из них последнее сочетание IEO следует также отбросить, потому что оно противоречит четвёртому правилу, именно в заключении больший термин берётся во всём объёме, как сказуемое отрицательного суждения, в то время как в большей посылке, как сказуемое или как подлежащее частно-утвердительного суждения, он взят не во всём объёме. Таким образом остаётся всего 11 сочетаний.
Если затем он проведёт остающиеся 11 сочетаний по четырём фигурам, то у него, кроме тех 19 сочетаний, которые приведены выше, останутся ещё 5 сочетаний, именно по 1-й фигуре AAI и EAO, по 2-й фигуре EAO и AEO и по 4-й фиг. AEO. Хотя эти 5 сочетаний дают правильное заключение, но их всё-таки следует отбросить, потому что они дают ослабленное или подчинённое заключение, именно они дают частное заключение, в то время как могут давать и общее. В самом деле, возьмём сочетание AAI по первой фигуре:
Все научные сведения полезны.
Химические сведения научны.
Некоторые химические сведения полезны.
Хотя это заключение правильно, но при данных посылках можно получить я общее заключение: «все химические сведения полезны». Поэтому данное сочетание следует считать практически бесполезным.
Таким образом, если мы отбросим эти 5 сочетаний, дающих ославленные заключения, то у нас останутся те 19 сочетаний, которые приведены выше.
Возьмём для иллюстрации фигур и модусов примеры.
Фигура 1.
Barbara
A: Все хищные животные питаются мясом.
A: Тигры суть хищные животные.
A: Тигры питаются мясом.
Этот силлогизм символически можно изобразить следующим образом. «Хищные животные» как средний термин обозначим при помощи M; «питающиеся мясом» как больший термин – посредством P, а «тигры» – посредством S; тогда силлогизм изобразится при помощи схемы на рис. 23.
Celarent
E: Ни одно насекомое не имеет более трёх пар ножек.
A: Пчёлы суть насекомые.
E: Пчёлы не имеют более трёх пар ножек.
Схема этого модуса изображена на рис. 24.
Darii
A: Все хищные животные питаются мясом.
I: Некоторые домашние животные суть хищные животные.
I: Некоторые домашние животные питаются мясом (рис, 25).
Ferio
E: Ни один невменяемый не наказуем.
I: Некоторые преступники невменяемы.
O: Некоторые преступники не наказуемы (рис. 26).
Фигура 2.
Cesare
E: Ни один справедливый человек не завистлив.
A: Всякий честолюбивый завистлив.
E: Ни один честолюбивый человек не есть справедлив (рис. 27).
Camestres
A: Преступники действуют из злого намерения.
E: N. не действовал из злого намерения.
E: N не есть преступник.
Festino
E: Ни один благоразумный человек не суеверен.
I: Некоторые хорошо образованные люди суеверны.
O: Некоторые хорошо образованные люди неблагоразумны.
Baroko
A: Все истинно моральные действия совершаются из правильных мотивов.
O: Некоторые действия, благодетельные для других, не совершаются из таких мотивов.
O: Некоторые благодетельные для других действия не суть истинно моральные.
Фигура 3.
Darapti
A: Все киты суть млекопитающие.
A: Все киты живут в воде.
I: Некоторые живущие в воде животные суть млекопитающие.
Данное умозаключение относится к фигуре 3, где средний термин d обеих посылках является подлежащим. Меньший термин «живущие в воде существа» взят в меньшей посылке не во всём объёме; следовательно, и в заключении должен быть взят не во всём объёме (рис. 28).
Felapton
E: Ни один глухонемой не может говорить.
A: Глухонемые суть духовно нормальные люди.
O: Некоторые духовно нормальные люди не могут говорить (рис. 29).
Disamis
I: Некоторые романы поучительны.
A: Все романы суть вымышленные рассказы.
I: Некоторые вымышленные рассказы поучительны.
Ferison
E: Ни одна несправедливая война не может быть оправдана.
I: Некоторые несправедливые войны были успешны.
O: Некоторые успешные войны не могут быть оправданы.
Фигура 4. Возьмём силлогизм:
Bramantip
A: Все металлы суть материальные вещи.
A: Все материальные вещи имеют тяжесть.
I: Некоторые тела, имеющие тяжесть, суть металлы.
В этом силлогизме средний термин взят сказуемым в большей и подлежащим в меньшей посылке. Сказуемое в меньшей посылке взято не во всём объёме, поэтому и в заключении оно должно быть взято не во всём объёме. Таким образом, получается заключение: «некоторые тела, имеющие тяжесть, суть металлы». Эта фигура называется галеновской от имени Галена (в III в. н. э.); её не было у Аристотеля.
Ещё пример для иллюстрации четвёртой фигуры.
Camenes
A: Все квадраты суть параллелограмм.
E: Ни один параллелограмм не есть треугольник.
E: Ни один треугольник не есть квадрат.
Характеристика фигур. Характеризуем в общих чертах все четыре фигуры силлогизма в отношении их познавательного значения.
Фигура 1. В ней меньшая посылка утвердительная, а большая общая (sit minor, affirmans, пёс major sit specialis). Эта фигура употребляется в тех случаях, когда нужно показать применение общих положений (аксиом, основоположений, законов природы, правовых норм и т.п.) к частным случаям; это есть фигура подчинения.
Фигура 2. В этой фигуре одна из посылок должна быть отрицательной и большая посылка должна быть общей (una negans esto, nec major sit specialis). Посредством этой фигуры отвергаются ложные дедукции, или ложные подчинения. Например, кто-нибудь утверждает относительно испытуемого газа, что он есть кислород. Нам стоит указать на какой-нибудь присущий кислороду признак, который не присущ испытуемому газу, для того чтобы убедиться в том, что это не есть кислород. Тогда у нас получится следующий силлогизм:
A: Кислород поддерживает горение
E: Этот газ не поддерживает горения.
E: Этот газ не есть кислород.
Кто-нибудь утверждает, что данное лицо больно лихорадкой; утверждая это, он производит подчинение. Нам нужно отвергнуть это подчинение. Тогда мы составляем следующий силлогизм:
A: Все больные лихорадкой испытывают жажду.
E: Этот больной не испытывает жажды.
E: Этот больной не болен лихорадкой.
Таким образом, по второй фигуре отвергаются ложные подчинения, и именно потому, что одна из посылок отрицательная. Юридические приговоры строятся по этой фигуре. Например:
A: Этот смертельный удар нанесён человеком, обладающим огромной силой.
E: Обвиняемый не есть человек, обладающий огромной силой.
E: Обвиняемый не нанёс смертельного удара.
Фигура 3. В фигуре 3 меньшая посылка должна быть утвердительной, а заключение должно быть частным (sit minor affirmans, conclusio sit specialis). Поэтому в фигуре 3 обыкновенно отвергается мнимая общность утвердительных и отрицательных суждений или доказывается исключение из общего положения. Положим, нам нужно доказать, что утверждение «все металлы твёрды» допускает исключение, что оно не всеобще. Тогда мы строим силлогизм по фигуре 3:
E: Ртуть не тверда.
A: Ртуть есть металл.
O: Некоторые металлы не твёрды.
Фигура 4 имеет искусственный характер и обыкновенно не употребляется.
Характер посылок и заключений каждой фигуры может быть наглядно представлен, если мы буквы модусов каждой фигуры расположим по вертикальным линиям таким образом, что буквы больших посылок будут идти по горизонтальной, буквы меньших посылок по второй горизонтальной и буквы заключений по третьей горизонтальной.
Вопросы для повторения
Чем обусловливается различие между фигурами силлогизма? Какие существуют фигуры силлогизма и какое различие между ними? Перечислите модусы всех четырёх фигур. Какое различие, между фигурами в отношения познания?